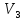98 Продовження таблиці 4.4
|
Елемент |
Значення |
Шлях |
Кількість шляхів |
|
|
|
1 – 4 – 6 – 8 – 9 – 12 – 14 1 – 2 – 6 – 9 – 11 – 12 – 14 1 – 3 – 6 – 9 – 11 – 12 – 14 1 – 4 – 6 – 9 – 11 – 12 – 14 1 – 2 – 5 – 6 – 9 – 11 – 14 1 – 2 – 5 – 6 – 9 – 12 – 14 1 – 3 – 5 – 6 – 9 – 11 – 14 1 – 3 – 5 – 6 – 9 – 12 – 14 1 – 2 – 6 – 8 – 12 – 13 – 14 1 – 2 – 6 – 9 – 12 – 13 – 14 1 – 3 – 6 – 8 – 12 – 13 – 14 1 – 2 – 6 – 10 – 12 – 13 – 14 1 – 3 – 6 – 9 – 12 – 13 – 14 1 – 4 – 6 – 8 – 12 – 13 – 14 1 – 3 – 6 – 1 – 12 – 13 – 14 1 – 4 – 6 – 9 – 12 – 13 – 14 1 – 4 – 6 – 10 – 12 – 13 – 14 1 – 2 – 5 – 6 – 10 – 12 – 1 4 1 – 2 – 5 – 6 – 10 – 13 – 14 1 – 3 – 5 – 6 – 10 – 12 – 14 1 – 3 – 5 – 6 – 10 – 13 – 14 |
|
Продовження таблиці 4.4
|
Елемент |
Значення |
Шлях |
Кількість шляхів |
|
|
|
1 – 2 – 3 – 6 – 7 – 10 – 12 – 14 1 – 2 – 3 – 6 – 7 – 10 – 13 – 14 1 – 2 – 3 – 6 – 8 – 10 – 12 – 14 1 – 2 – 4 – 6 – 7 – 10 – 12 – 14 1 – 2 – 3 – 6 – 8 – 10 – 13 – 14 1 – 2 – 4 – 6 – 7 – 10 – 13 – 14 1 – 2 – 4 – 6 – 8 – 10 – 12 – 14 1 – 2 – 5 – 6 – 7 – 10 – 12 – 14 1 – 2 – 4 – 6 – 8 – 10 – 13 – 14 1 – 2 – 5 – 6 – 7 – 10 – 13 – 14 1 – 2 – 5 – 6 – 8 – 10 – 12 – 14 1 – 3 – 5 – 6 – 7 – 10 – 12 – 14 1 – 2 – 5 – 6 – 8 – 10 – 13 – 14 1 – 3 – 5 – 6 – 7 – 10 – 13 – 14 1 – 3 – 5 – 6 – 8 – 10 – 12 – 14 1 – 3 – 5 – 6 – 8 – 10 – 13 – 14 1 – 2 – 3 – 6 – 9 – 11 – 12 – 14 1 – 2 – 4 – 6 – 9 – 11 – 12 – 14 1 – 2 – 5 – 6 – 9 – 11 – 12 – 14 |
50 |
99
100
|
Елемент |
Значення |
Шлях |
Кількість шляхів |
|
|
|
1 – 3 – 5 – 6 – 9 – 11 – 12 – 14 1 – 2 – 3 – 6 – 8 – 9 – 11 – 14 1 – 2 – 3 – 6 – 8 – 9 – 12 – 14 1 – 2 – 4 – 6 – 8 – 9 – 11 – 14 1 – 2 – 4 – 6 – 8 – 9 – 12 – 14 1 – 2 – 5 – 6 – 8 – 9 – 11 – 14 1 – 2 – 5 – 6 – 8 – 9 – 12 – 14 1 – 3 – 5 – 6 – 8 – 9 – 11 – 14 1 – 3 – 5 – 6 – 8 – 9 – 12 – 14 1 – 2 – 3 – 6 – 8 – 12 – 13 – 14 1 – 2 – 3 – 6 – 9 – 12 – 13 – 14 1 – 2 – 4 – 6 – 8 – 12 – 13 – 14 1 – 2 – 3 – 6 – 10 – 12 – 13 – 14 1 – 2 – 4 – 6 – 9 – 12 – 13 – 14 1 – 2 – 5 – 6 – 8 – 12 – 13 – 14 1 – 2 – 4 – 6 – 10 – 12 – 13 – 14 1 – 2 – 5 – 6 – 9 – 12 – 13 – 14 1 – 3 – 5 – 6 – 8 – 12 – 13 – 14 1 – 2 – 5 – 6 – 10 – 12 – 13 – 14 1 – 3 – 5 – 6 – 9 – 12 – 13 – 14 1 – 3 – 5 – 6 – 10 – 12 – 13 – 14 |
|
Продовження таблиці 4.4
|
Елемент |
Значення |
Шлях |
Кількість шляхів |
|
|
|
1 – 2 – 6 – 8 – 9 – 11 – 12 – 14 1 – 3 – 6 – 8 – 9 – 11 – 12 – 14 1 – 2 – 6 – 8 – 9 – 12 – 13 – 14 1 – 4 – 6 – 8 – 9 – 11 – 12 – 14 1 – 2 – 6 – 8 – 10 – 12 – 13 – 14 1 – 3 – 6 – 8 – 9 – 12 – 13 – 14 1 – 3 – 6 – 8 – 10 – 12 – 13 – 14 1 – 4 – 6 – 8 – 9 – 12 – 13 – 14 1 – 4 – 6 – 8 – 10 – 12 – 13 – 14 1 – 2 – 3 – 5 – 6 – 9 – 12 – 14 |
|
101
Також згідно завдання необхідно за допомогою алгоритму Дейкстри знайти шлях мінімальної довжини між 1 та 14 та його довжину.
Алгоритм Дейкстри (Dijkstra’s algorithm) – алгоритм на графах, винайдений нідерландським вченим Е. Дейкстрой в 1959 році. Даний алгоритм знаходить найкоротшу відстань від однієї з вершин графа до всіх інших. Алгоритм працює тільки для графів без ребер від’ємної ваги. Алгоритм широко застосовується в програмуванні й технологіях, наприклад, його використовує протокол OSPF для усунення кільцевих маршрутів.
Завдання
побудови найкоротшого шляху між заданою
парою вершин
 і
і
 полягає в тому, щоб з множини шляхів, що
сполучають вказані вершини, знайти
такий, сумарна довжина дуг якого є
мінімальною.
полягає в тому, щоб з множини шляхів, що
сполучають вказані вершини, знайти
такий, сумарна довжина дуг якого є
мінімальною.
Алгоритм Дейкстри можна описати наступними кроками.
Крок
1. Перед початком виконання алгоритму
всі вершини не помічені. Кожній вершині
 в ході виконання алгоритму привласнюється
число
в ході виконання алгоритму привласнюється
число
 ,
рівне довжині найкоротшого шляху з
,
рівне довжині найкоротшого шляху з
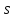 в
в
 ,
що включає тільки помічені вершини.
,
що включає тільки помічені вершини.
Покласти
 ,
,
 для всіх
для всіх
 ,
відмінних від
,
відмінних від
 .
Помітити вершину
.
Помітити вершину
 і покласти
і покласти
 (
( – остання із помічених вершин).
– остання із помічених вершин).
Крок
2. Для кожної непоміченої вершини
 ,
таким чином перерахувати величину
,
таким чином перерахувати величину
 :
:
|
|
(4.1) |
Якщо
 для всіх непомічених вершин
для всіх непомічених вершин
 ,
закінчити процедуру алгоритму: у заданому
графі відсутні шляхи між вказаною парою
вершин. Інакше помітити ту з вершин
,
закінчити процедуру алгоритму: у заданому
графі відсутні шляхи між вказаною парою
вершин. Інакше помітити ту з вершин
 ,
для якої величина
,
для якої величина
 є найменшою. Покласти
є найменшою. Покласти
 .
.
Крок
3. Якщо
 ,
закінчити процедуру: найкоротший шлях
з вершини
,
закінчити процедуру: найкоротший шлях
з вершини
 в вершину
в вершину
 знайдено. Інакше перейти до кроку 2.
знайдено. Інакше перейти до кроку 2.
Проведемо
ініціалізацію для виконання алгоритму
Дейкстри. Відстань до всіх вершин графа
встановлюємо рівною
 .
Відстань до
.
Відстань до
 .
Жодна вершина графа ще не опрацьована.
.
Жодна вершина графа ще не опрацьована.

Рисунок 4.10 – Початкова ініціалізація для виконання алгоритму Дейкстри
Знаходимо
таку вершину (із ще не оброблених),
поточна найкоротша відстань до якої
мінімальна. В нашому випадку це вершина
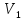 .
.
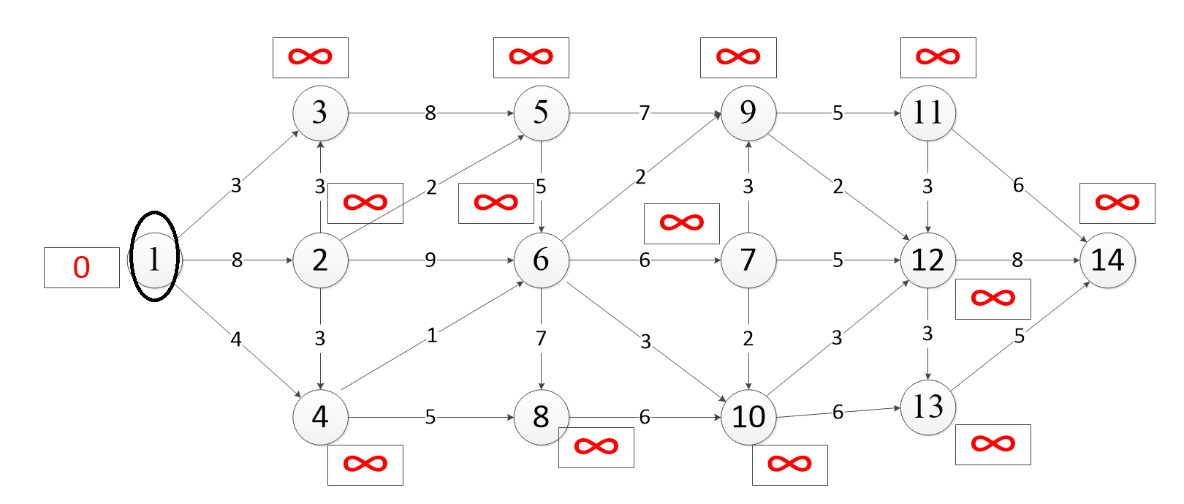
Рисунок
4.11 – Обрана поточна вершина

Обходимо
всіх її сусідів: якщо шлях в сусідню
вершину через
 менший за поточний мінімальний шлях до
даної сусідньої вершини, то запам’ятовуємо
знайдений новий, коротший шлях як
поточний найкоротший шлях до сусіда.
менший за поточний мінімальний шлях до
даної сусідньої вершини, то запам’ятовуємо
знайдений новий, коротший шлях як
поточний найкоротший шлях до сусіда.
Один
з сусідів вершини
 – це вершина
– це вершина
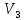 .
Шлях до неї через
.
Шлях до неї через
 дорівнює сумі найкоротшої відстані до
дорівнює сумі найкоротшої відстані до
 та довжина дуги між вершинами
та довжина дуги між вершинами
 та
та
 ,
тобто 0 + 3 = 3. Отримане значення менше
поточного найкоротшого шляху до вершини
,
тобто 0 + 3 = 3. Отримане значення менше
поточного найкоротшого шляху до вершини
 ,
тому найкоротший шлях до неї стає рівним
3.
,
тому найкоротший шлях до неї стає рівним
3.
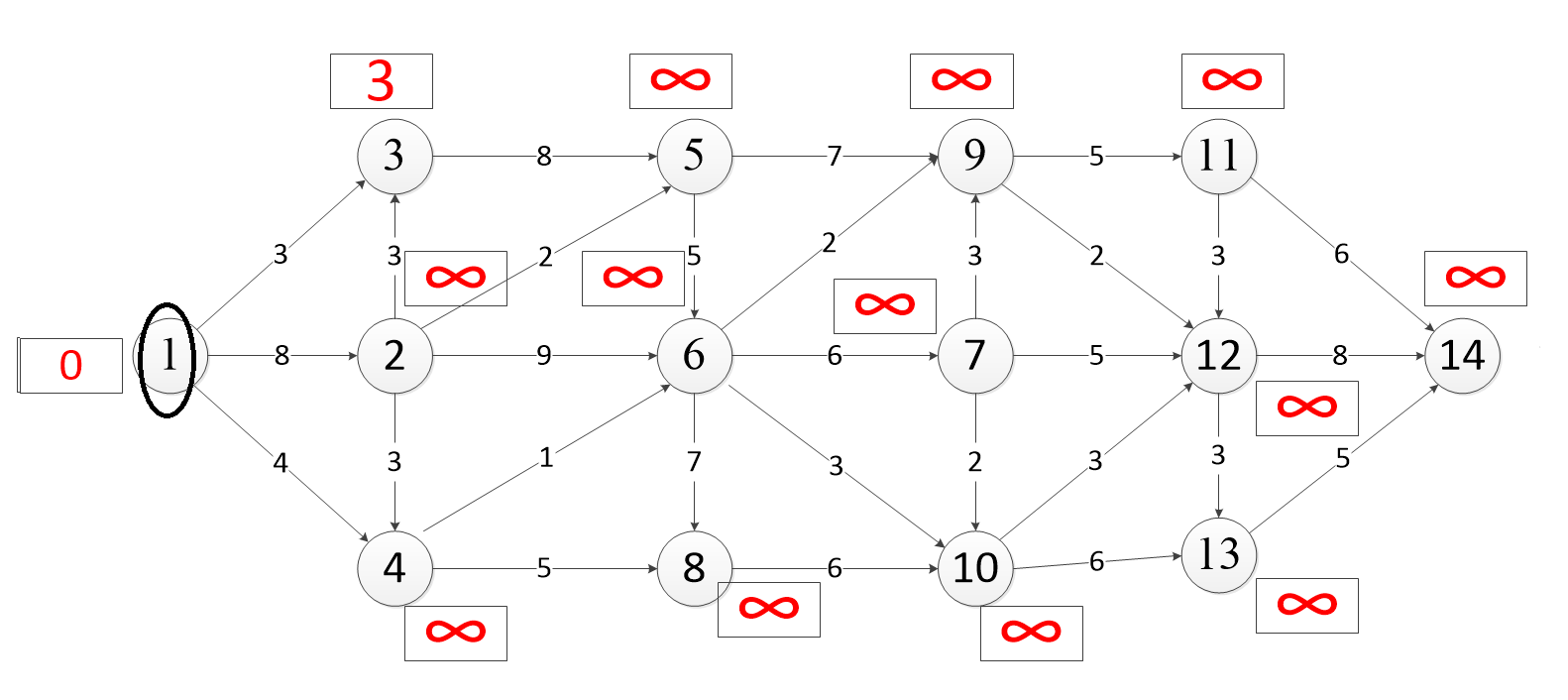
Рисунок
4.12 – Обчислення найкоротшого шляху до
вершини
 через
через

Аналогічну
операцію виконуємо з двома іншими
сусідами
 ,
а саме вершинами
,
а саме вершинами
 та
та
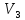 :
:

Рисунок
4.13 – Обчислення найкоротшого шляху до
вершин
 та
та
 через
через

Всі
сусіди вершини
 перевірені. Поточна мінімальна відстань
до вершини
перевірені. Поточна мінімальна відстань
до вершини
 вважається остаточною та обговоренню
не підлягає (вперше це довів Дейкстра).
Тому викреслимо
вважається остаточною та обговоренню
не підлягає (вперше це довів Дейкстра).
Тому викреслимо
 з графа, щоб відмітити даний факт.
з графа, щоб відмітити даний факт.

Рисунок
4.14 – Викреслення вершини
 з графу
з графу
Після
чого відбувається повернення до кроку
2 алгоритму. Знову знаходимо «найближчу»
необроблену (невикреслену) вершину.
Такою є вершина
 з поточною найкоротшою відстанню рівною
3. Розглянемо цю вершину.
з поточною найкоротшою відстанню рівною
3. Розглянемо цю вершину.

Рисунок
4.15 – Обрана поточною вершина

Знову
ж таки намагаємося зменшити відстань
до всіх сусідів вершини
 ,
проходячи в них через
,
проходячи в них через
 .
Сусідами вершини
.
Сусідами вершини
 є вершина:
є вершина:
 Вершина
Вершина
 :
якщо йти в неї через
:
якщо йти в неї через
 ,
то шлях буде рівний сумі найкоротшої
відстані до
,
то шлях буде рівний сумі найкоротшої
відстані до
 та відстань між вершинами
та відстань між вершинами
 та
та
 і складе
і складе
 .
.
Також
розглядаємо вершини
 та
та
 .
Шляхи відповідно складають 8 та 4, тому
далі переходимо до вершини
.
Шляхи відповідно складають 8 та 4, тому
далі переходимо до вершини


Рисунок
4.16 – Обрана поточною вершина


Рисунок
4.17 – Обрана поточною вершина
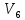

Рисунок
4.18 – Обрана поточною вершина


Рисунок
4.19 – Обрана поточною вершина


Рисунок
4.20 – Обрана поточною вершина


Рисунок
4.21 – Обрана поточною вершина


Рисунок
4.22 – Обрана поточною вершина


Рисунок
4.23 – Обрана поточною вершина


Рисунок
4.24 – Обрана поточною вершина


Рисунок
4.25 – Обрана поточною вершина


Рисунок
4.26 – Викреслення останньої вершини

Алгоритм
закінчує роботу, коли викреслені всі
вершини. Результат його роботи видно
на рис. 4.27: найкоротший шлях від вершини
 до
до
 складає 17. При цьому він проходить по
вершинах
складає 17. При цьому він проходить по
вершинах
 –
–
 –
–
 –
–
 –
–
 –
–
 .
.

Рисунок
4.27 – Найкоротший шлях між
 та
та
 (за алгоритмом Дейкстри)
(за алгоритмом Дейкстри)
За алгоритмом Флойда необхідно знайти всі найкоротші шляхи. Алгоритм Флойда-Уоршелла – це алгоритм динамічного програмування для знаходження найкоротших відстаней між усіма вершинами зваженого орієнтованого графа. Розроблений в 1962 році Робертом Флойдом і Стівеном Воршеллом, хоча в 1959 р. Бернард Рой (Bernard Roy) опублікував практично такий же алгоритм, але це залишилося непоміченим.
Нехай
вершини графа
 пронумеровані від 1 до n і введемо
позначення
пронумеровані від 1 до n і введемо
позначення
 для довжини найкоротшого шляху від i
до
j,
який окрім самих вершин i
та
j
проходить тільки через вершини
для довжини найкоротшого шляху від i
до
j,
який окрім самих вершин i
та
j
проходить тільки через вершини
 .Очевидно,
що
.Очевидно,
що
 – довжина (вага) ребра
– довжина (вага) ребра
 ,
якщо таке існує (в іншому випадку його
довжина може бути позначена як ∞).
,
якщо таке існує (в іншому випадку його
довжина може бути позначена як ∞).
В основі алгоритму лежать дві властивості найкоротшого шляху графа:
-
Нехай
 найкоротший шлях від вершини
найкоротший шлях від вершини
 до вершини
до вершини
 ,
а також його підшлях
,
а також його підшлях
 ,
при цьому діє
,
при цьому діє
 .
.
Якщо
 – найкоротший шлях від
– найкоротший шлях від
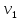 до
до
 ,
то
,
то
 також є найкоротшим шляхом від вершини
також є найкоротшим шляхом від вершини
 до
до
 .
.
Доведення:
вартість шляху
 складається з вартості шляху
складається з вартості шляху
 та вартості інших його частин, якщо є
більш короткий шлях за
та вартості інших його частин, якщо є
більш короткий шлях за
 ,
то довжина шляху
,
то довжина шляху
 зменшиться, що призведе до протиріччя
з твердженням, що шлях і так вже э
найкоротшим.
зменшиться, що призведе до протиріччя
з твердженням, що шлях і так вже э
найкоротшим.
-
Друга властивість є основою алгоритму. Шлях
 від
від
 до
до
 ,
що проходить через певну множину
дозволених вершин, обмежений індексом
k.
,
що проходить через певну множину
дозволених вершин, обмежений індексом
k.
Тобто
якщо
 ,
то ми розглядаємо прямі з’єднання
вершин однієї з одною, так як множина
дозволених проміжних вершин рівна нулю.
Якщо ж
,
то ми розглядаємо прямі з’єднання
вершин однієї з одною, так як множина
дозволених проміжних вершин рівна нулю.
Якщо ж
 – ми розглядаємо шляхи, що проходять
через вершину
– ми розглядаємо шляхи, що проходять
через вершину
 ,
при
,
при
 – через вершини
– через вершини
 ,
а при
,
а при
 –
–
 і так далі.
і так далі.
Існує два варіанти
значення
 :
:
-
найкоротший шлях між
 до
до
 не проходить через вершину
не проходить через вершину
 ,
тобто від додавання додаткової вершини
ми нічого не виграємо і нічого не
змінимо, а отже вартість найкоротшого
шляху
,
тобто від додавання додаткової вершини
ми нічого не виграємо і нічого не
змінимо, а отже вартість найкоротшого
шляху
 не змінилася, відповідно
не змінилася, відповідно
 ;
; -
існує більш короткий шлях між
 до
до
 ,
що проходить через
,
що проходить через
 ,
тоді він спочатку йде від
,
тоді він спочатку йде від
 до
до
 ,
а потім від
,
а потім від
 до
до
 .
У цьому випадку, очевидно,
.
У цьому випадку, очевидно,
 .
.
Таким чином, для
знаходження значення функції досить
вибрати мінімум з двох позначених
значень. Тоді рекурентна
формула для
 має вигляд:
має вигляд:
-
 – довжина ребра
– довжина ребра
 ;
; -
 .
.
Алгоритм
Флойда-Уоршелла послідовно обчислює
всі значення
 ,
для k
від 1 до n.
Отримані значення
,
для k
від 1 до n.
Отримані значення
 є довжинами найкоротших шляхів між
вершинами
є довжинами найкоротших шляхів між
вершинами
 .
.
На кожному кроці
алгоритм генерує матрицю
 Матриця
Матриця
 містить довжини найкоротших шляхів між
усіма вершинами графа. Перед роботою
алгоритму матриця заповнюється довжинами
ребер графа.
містить довжини найкоротших шляхів між
усіма вершинами графа. Перед роботою
алгоритму матриця заповнюється довжинами
ребер графа.
Передбачається, що якщо між двома якимись вершинами немає ребра, то в матриці суміжності буде записано певне велике число (досить велике, щоб воно було більше довжини будь-якого шляху в даному графі); тоді це ребро завжди буде невигідно брати, і алгоритм спрацює правильно. Правда, якщо не вжити спеціальних заходів, то при наявності в графі ребер негативної ваги, в результуючої матриці можуть з’явитися числа виду ∞-1, ∞-2, і т.д., які, звичайно, як і раніше означають, що між відповідними вершинами взагалі немає шляху. Тому при наявності в графі негативних ребер алгоритм Флойда- Уоршелла краще написати так, щоб він не виконував переходи з тих станів, в яких вже стоїть помітка «немає шляху».
Побудуємо першу матрицю D0, яка буде співпадати з матрицею відстаней нашого графу:
Таблиця 4.5 – Перший крок алгоритму Флойда-Уоршелла (матриця D0)
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
1 |
0 |
8 |
3 |
4 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
|
2 |
∞ |
0 |
3 |
3 |
2 |
9 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
|
3 |
∞ |
∞ |
0 |
∞ |
8 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
|
4 |
∞ |
∞ |
∞ |
0 |
∞ |
1 |
∞ |
5 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
|
5 |
∞ |
∞ |
∞ |
∞ |
0 |
5 |
∞ |
∞ |
7 |
∞ |
∞ |
∞ |
∞ |
∞ |
|
6 |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
6 |
7 |
2 |
3 |
∞ |
∞ |
∞ |
∞ |
|
7 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
3 |
2 |
∞ |
5 |
∞ |
∞ |
|
8 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
6 |
∞ |
∞ |
∞ |
∞ |
|
9 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
5 |
2 |
∞ |
∞ |
|
10 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
3 |
6 |
∞ |
|
11 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
3 |
∞ |
6 |
|
12 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
3 |
8 |
|
13 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
5 |
|
14 |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
Відобразимо матрицю з довжинами найкоротших шляхів між всіма вершинами нашого графу:
Таблиця 4.6 – Останній крок алгоритму Флойда-Уоршелла (матриця Dn)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
8 |
3 |
4 |
10 |
5 |
11 |
9 |
7 |
8 |
12 |
9 |
12 |
17 |
|
|
∞ |
0 |
3 |
3 |
2 |
4 |
10 |
8 |
6 |
7 |
11 |
8 |
11 |
16 |
|
|
∞ |
∞ |
0 |
∞ |
8 |
13 |
19 |
20 |
15 |
16 |
20 |
17 |
20 |
25 |
|
|
∞ |
∞ |
∞ |
0 |
∞ |
1 |
7 |
5 |
3 |
4 |
8 |
5 |
8 |
13 |
|
|
∞ |
∞ |
∞ |
∞ |
0 |
5 |
11 |
12 |
7 |
8 |
12 |
9 |
12 |
17 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
6 |
7 |
2 |
3 |
7 |
4 |
7 |
12 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
3 |
2 |
8 |
5 |
8 |
13 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
6 |
∞ |
9 |
12 |
17 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
5 |
2 |
5 |
10 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
∞ |
3 |
6 |
11 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
3 |
6 |
6 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
3 |
8 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
5 |
|
|
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
∞ |
0 |
 Таблиця
4.7 – Матриця переходів згідно останнього
кроку алгоритму
Флойда-Уоршелла
Таблиця
4.7 – Матриця переходів згідно останнього
кроку алгоритму
Флойда-Уоршелла
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
1 |
- |
1-2 |
1-3 |
1-4 |
1-2-5 |
1-4-6 |
1-4-6-7 |
1-4-8 |
1-4-6-9 |
1-4-6-10 |
1-4-6-9-11 |
1-4-6-9-12 |
1-4-6-9-12-13 |
1-4-6-9-12-14 |
|
2 |
- |
- |
2-3 |
2-4 |
2-5 |
2-4-6 |
2-4-6-7 |
2-4-8 |
2-4-6-9 |
2-4-6-10 |
2-4-6-9-11 |
2-4-6-9-12 |
2-4-6-9-12-13 |
2-4-6-9-12-14 |
|
3 |
- |
- |
- |
- |
3-5 |
3-5-6 |
3-5-6-7 |
3-5-6-8 |
3-5-9 |
3-5-6-10 |
3-5-9-11 |
3-5-9-12 |
3-5-9-12-13 |
3-5-9-12-14 |
|
4 |
- |
- |
- |
- |
- |
4-6 |
4-6-7 |
4-8 |
4-6-9 |
4-6-10 |
4-6-9-11 |
4-6-9-12 |
4-6-9-12-13 |
4-6-9-12-14 |
|
5 |
- |
- |
- |
- |
- |
5-6 |
5-6-7 |
5-6-8 |
5-9 |
5-6-10 |
5-9-11 |
5-9-12 |
5-9-12-13 |
5-9-12-14 |
|
6 |
- |
- |
- |
- |
- |
- |
6-7 |
6-8 |
6-9 |
6-10 |
6-9-11 |
6-9-12 |
6-9-12-13 |
6-9-12-14 |
|
7 |
- |
- |
- |
- |
- |
- |
- |
- |
7-9 |
7-10 |
7-9-11 |
7-12 |
7-10-13 |
7-12-14 |
114
 Продовження
таблиці 4.7
Продовження
таблиці 4.7
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
8 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8-10 |
- |
8-10-12 |
8-10-13 |
8-10-12-14 |
|
9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
9-11 |
9-12 |
9-12-13 |
9-12-14 |
|
10 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
10-12 |
10-13 |
10-12-14 |
|
11 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
11-12 |
11-12-13 |
11-14 |
|
12 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
12-13 |
12-14 |
|
13 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
13-14 |
|
14 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
115
Матриця
відстаней показує нам найкоротшу
(найдешевшу) відстань для будь-якої пари
вершин, а дізнатися шлях можна, якщо при
розрахунку
 розрахувати ще й
розрахувати ще й
 .
При цьому
.
При цьому
 – це попередник вершини
– це попередник вершини
 на шляху від
на шляху від
 з множиною дозволених проміжних вершин
з множиною дозволених проміжних вершин
 :
:
|
|
(4.2) |
Реконструюємо
оптимальний шлях
використовуючи
матрицю переходів
 (табл. 4.7). Для цього з кінця шляху
(табл. 4.7). Для цього з кінця шляху
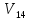 будемо переходити до початку
будемо переходити до початку
 .
.

 Таблиця
4.7 – Матриця переходів згідно останнього
кроку алгоритму
Флойда-Уоршелла
Таблиця
4.7 – Матриця переходів згідно останнього
кроку алгоритму
Флойда-Уоршелла
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
2 |
|
6 |
6 |
4 |
7 |
6 |
|
11 |
|
|
|
2 |
2 |
2 |
2 |
2 |
4 |
5 |
6 |
4 |
7 |
6 |
7 |
11 |
12 |
|
|
3 |
3 |
3 |
3 |
3 |
5 |
5 |
6 |
6 |
7 |
6 |
7 |
11 |
12 |
|
|
4 |
4 |
4 |
4 |
4 |
4 |
6 |
6 |
4 |
7 |
6 |
7 |
11 |
12 |
|
|
5 |
5 |
5 |
5 |
5 |
5 |
5 |
6 |
6 |
7 |
6 |
7 |
11 |
12 |
|
|
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
7 |
6 |
7 |
11 |
12 |
|
|
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
7 |
12 |
12 |
|
|
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
8 |
11 |
12 |
|
|
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
9 |
11 |
11 |
13 |
|
|
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
12 |
10 |
|
|
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
11 |
13 |
|
|
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
|
|
13 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
13 |
|
|
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
14 |
Згідно
 ,
а отже оптимальний шлях проходить через
ребро
,
а отже оптимальний шлях проходить через
ребро
 .
У вершину
.
У вершину
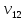 ми потрапили з вершини
ми потрапили з вершини
 (
( )
і т.д.
)
і т.д.
Отже
найкоротший шлях з вершини
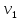 у вершину
у вершину
 за алгоритмом Флойда-Уоршелла наступний:
за алгоритмом Флойда-Уоршелла наступний:
|
|
(4.3) |
Як
видно з рисунку 4.28 найкоротші шляхи між
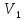 та
та
 за алгоритмами Флойда-Уоршелла та
Дейкстри співпали:
за алгоритмами Флойда-Уоршелла та
Дейкстри співпали:

Рисунок
4.28 – Найкоротший шлях між
 та
та
 (за алгоритмом Флойда-Уоршелла)
(за алгоритмом Флойда-Уоршелла)
В
нашому випадку маємо зв’язний граф, в
якому виділено дві вершини:
 – джерело (
– джерело ( ),
),
 – стік (
– стік ( ).
Кожній дузі
).
Кожній дузі
 графа поставлено у відповідність
невід’ємне число
графа поставлено у відповідність
невід’ємне число
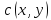 ,
яке інтерпретується як максимальна
кількість одиниць деякого товару, яке
може бути доставлено з вершини
,
яке інтерпретується як максимальна
кількість одиниць деякого товару, яке
може бути доставлено з вершини
 в вершину
в вершину
 за одиницю часу. Дане число прийнято
називати пропускною здатністю дуги.
Такий граф називають мережею, а його
вершини – вузлами.
за одиницю часу. Дане число прийнято
називати пропускною здатністю дуги.
Такий граф називають мережею, а його
вершини – вузлами.
Мережевий графік – це граф, який відображає роботи проекту, зв’язки між ними, стану проекту.
Може будуватися в 2-х варіантах:
-
вершини графа відображають стани деякого об’єкта, а дуги – роботи, що ведуться на даному об’єкті.
-
вершини графа відображають роботи, а зв’язки між ними – залежності між роботами.
При побудові мережевого графіка необхідно дотримуватися ряду правил:
-
у мережевій моделі не повинно бути «глухих кутів», тобто подій, з яких не виходить жодна робота, за винятком завершального події. В протилежному випадку або робота не потрібна і її необхідно анулювати, або не помічена необхідність наступної роботи, за даною подією, для звершення певної наступної події. У таких випадках необхідно ретельне вивчення взаємозв’язків подій і робіт для виправлення непорозуміння, що виникло;
-
в мережевому графіку не повинно бути «хвостових» подій (крім вихідної), яким не передує хоча б одна робота. Виявивши в мережі такі події, необхідно визначити виконавців попередніх їм робіт і включити дані роботи в мережу;
-
у мережі не повинно бути замкнутих контурів і петель, тобто шляхів, що з’єднують деякі події з ними ж самими. При виникненні контуру (а в складних мережах, тобто в мережах з високим показником складності, це зустрічається досить часто і виявляється лише за допомогою ЕОМ) необхідно повернутися до вихідних даних і шляхом перегляду складу робіт домогтися його усунення;
-
будь-які дві події повинні бути безпосередньо пов’язані не більш ніж однією роботою-стрілкою. Порушення цієї умови відбувається при зображенні паралельно виконуваних робіт. Якщо ці роботи так і залишити, то відбудеться плутанина через те, що дві різні роботи будуть мати одне і те ж позначення. Проте зміст даних робіт, склад залучених виконавців і кількість витрачених на роботи ресурсів можуть істотно відрізнятися.
Шлях – це будь-яка послідовність робіт, якщо кінцева подія кожної роботи є початковою подією наступної роботи. Завершений шлях – це будь-який шлях , початком якого є вихідна подія, а закінченням – завершальна. Термін шляху дорівнює сумі всіх термінів виконання робіт, які створюють шлях. Завершений шлях з найбільшим терміном серед усіх завершених шляхів називається критичним шляхом.
Роботи, які його створюють, називаються критичними. Граф може мати не один критичний шлях. Максимальним шляхом між двома подіями «i» та «j» називається шлях від i-ої події до j-ої, який має максимальний термін, тобто сума термінів робіт, які складають такий шлях, є не меншою ніж відповідна сума для довільного шляху від i-ої події до j-ої.
Якщо граф має велику кількість подій ( до двох десятків), то результати можна записувати на графові за схемою зображеною на рис. 4.53.

Рисунок 4.29 – Схема термінів
Для обчислення ранніх термінів tp(i) звершення подій вершини графу використовується формула:
 (4.4)
(4.4)
Формула
(4.4) показує, що обчислення параметру
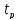 доцільно починати з вихідної події, для
якої
доцільно починати з вихідної події, для
якої
 дорівнює нулю, розглядаючи наступні
події в порядку збільшення їх номерів.
дорівнює нулю, розглядаючи наступні
події в порядку збільшення їх номерів.
Піздній
(або граничний) термін (строк)
 завершення і-ої події обчислюється за
формулою:
завершення і-ої події обчислюється за
формулою:
 (4.5)
(4.5)
Резерв часу R(i) i-ої події обчислюється як різниця пізнього та раннього термінів завершення і-ої події:
 (4.6)
(4.6)
Резерв часу подій показує, на який допустимий термін можна затримати завершення події, не гальмуючи при цьому термін виконання всього комплексу робіт мережі.
Результати розрахунків параметрів подій графу занесемо в таблицю 4.8.
Таблиця 4.8 – Результати розрахунків параметрів подій графу
|
№ події |
tp – ранній термін завершення події |
tn – пізній термін завершення події |
Rp – резерв часу події |
|
1 |
0 |
min {8; 0; 19} = 0 |
0 |
|
2 |
0+8 = 8 |
min {8; 17; 15;20} = 8 |
0 |
|
3 |
max {11; 3}=11 |
19 - 8 = 11 |
0 |
|
4 |
max {11; 4}=11 |
min {23; 27} = 23 |
12 |
|
5 |
max {10; 19}=19 |
min {19; 26} = 19 |
0 |
|
6 |
max {24; 17; 12}=24 |
min {25; 35; 24; 31} = 24 |
0 |
|
7 |
24+6=30 |
min {36; 30; 36} = 30 |
0 |
|
8 |
max {34; 16}=31 |
38 – 6 = 32 |
1 |
|
9 |
max {26; 33; 33}=33 |
min {33; 39} = 33 |
0 |
|
10 |
max {37; 27; 32}=37 |
min {38; 38} = 38 |
1 |
|
11 |
33+5=38 |
min {38; 43} = 38 |
0 |
|
12 |
max {41; 35; 35; 40}=41 |
min {41; 41} = 41 |
0 |
|
13 |
max {44; 43}=44 |
49 – 5 = 44 |
0 |
|
14 |
max {44; 49; 49}=49 |
49 |
0 |

Рисунок – 4.30 – Результат обчислення параметрів часу подій та критичного шляху графу
Наступним кроком буде розрахунок параметрів робіт.
Ранній термін початку роботи співпадає з раннім терміном здійснення попередньої події і, тому:
 (4.7)
(4.7)
Таким чином, раній термін tpn(i,j) завершення роботи (i,j) обчислюється так:
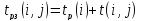 (4.8)
(4.8)
Для того, щоб фактичний термін виконання певної роботи не збільшив час виконання комплексу робіт, повинна виконуватись вимога: кожну роботу слід завершувати не пізніше допустимого терміну її завершувати не пізніше допустимого терміну її завершальної події j. За таких умов пізній термін tпз(i,j) завершення роботи (i,j) визначається формулою:
 (4.9)
(4.9)
а пізній термін tпп(i,j) початку цієї роботи – формулою:
 (4.10)
(4.10)
Розглянемо резерви часу шляхів. Такі резерви мають всі некритичні шляхи. Резерв часу Rt(L) шляху L визначається як різниця термінів критичного та даного шляхів:
 (4.11)
(4.11)
Величина Rt(L) показує на скільки можуть бути збільшені в сумі терміни всіх робіт, які складають шлях L.
Повний резерв Rn(i,j) часу роботи (i,j) обчислюэться за формулою:
 (4.12)
(4.12)
Частним резервом першого виду R1 часу роботи є та частина повного резерву часу цієї роботи, на яку можна збільшити термін роботи, не змінивши при цьому пізній термін її початкової події. Цим резервом можна скористатися при виконанні певної роботи за умови, що її початкова та завершальні події відбудуться в свої пізні терміни. Величина R(i,j) обчислюється за формулою:
 (4.13)
(4.13)
Незалежним резервом часу Rn роботи (i,j) є та частина повного резерву часу цієї роботи, яка визначається за умови, що попередні роботи завершуються в пізні терміни, а всі наступні розпочинаються в ранні терміни. Величина Rн обчислюється за наступною формулою:
 (4.14)
(4.14)
Незалежний резерв часу має сенс лише для тих робіт, які не належать максимальним шляхам, що проходять через її початкові та завершальні події.
Таблиця 4.9 – Розраховані резерви часу
|
Роботи |
Терміни робіт |
tрп |
tрз |
tпп |
tпз |
Rn |
R1 |
Rн |
|
1;2 |
8 |
0 |
8 |
0 |
8 |
0 |
0 |
0 |
|
1;3 |
3 |
0 |
3 |
8 |
11 |
8 |
8 |
8 |
|
1;4 |
4 |
0 |
4 |
19 |
23 |
19 |
19 |
7 |
|
2;3 |
3 |
8 |
11 |
8 |
11 |
0 |
0 |
0 |
|
2;4 |
3 |
8 |
11 |
20 |
23 |
12 |
12 |
0 |
|
2;5 |
2 |
8 |
10 |
17 |
19 |
9 |
9 |
9 |
|
2;6 |
9 |
8 |
17 |
15 |
24 |
7 |
7 |
7 |
|
3;5 |
8 |
11 |
19 |
11 |
19 |
0 |
0 |
0 |
|
4;6 |
1 |
11 |
12 |
23 |
24 |
12 |
0 |
0 |
|
4;8 |
5 |
11 |
16 |
27 |
32 |
16 |
4 |
3 |
|
5;6 |
5 |
19 |
24 |
19 |
24 |
0 |
0 |
0 |
|
5;9 |
7 |
19 |
26 |
26 |
33 |
7 |
7 |
7 |
|
6;7 |
6 |
24 |
30 |
24 |
30 |
0 |
0 |
0 |
|
6;8 |
7 |
24 |
31 |
25 |
32 |
1 |
1 |
0 |
|
6;9 |
2 |
24 |
26 |
31 |
33 |
7 |
7 |
7 |
|
6;10 |
3 |
24 |
27 |
35 |
38 |
11 |
11 |
10 |
|
7;10 |
2 |
30 |
32 |
36 |
38 |
6 |
6 |
5 |
|
7;9 |
3 |
30 |
33 |
30 |
33 |
0 |
0 |
0 |
|
7;12 |
5 |
30 |
35 |
36 |
41 |
6 |
6 |
6 |
|
8;10 |
6 |
31 |
37 |
32 |
38 |
1 |
0 |
-1 |
|
9;11 |
5 |
33 |
38 |
33 |
38 |
0 |
0 |
0 |
|
9;12 |
2 |
33 |
35 |
39 |
41 |
6 |
6 |
6 |
|
10;12 |
3 |
37 |
40 |
38 |
41 |
1 |
0 |
0 |
|
10;13 |
6 |
37 |
43 |
38 |
44 |
1 |
0 |
0 |
|
11;12 |
3 |
38 |
41 |
38 |
41 |
0 |
0 |
0 |
|
11;14 |
6 |
38 |
44 |
43 |
49 |
5 |
5 |
5 |
|
12;13 |
3 |
41 |
44 |
41 |
44 |
0 |
0 |
0 |
|
12;14 |
8 |
41 |
49 |
41 |
49 |
0 |
0 |
0 |
|
13;14 |
5 |
44 |
49 |
44 |
49 |
0 |
0 |
0 |
Коефіцієнтом напруженості K(i,j) називається відношення тривалості незбіжних (укладених між одними і тими ж подіями) відрізків шляху, одним з яких є шлях максимальної тривалості, що проходить через дану роботу, а іншим - критичний шлях:
 (4.15)
(4.15)
Коефіцієнт напруженості може змінюватися в межах від 0 (для робіт, у яких відрізки максимального із шляхів, що не збігаються з критичним шляхом, складаються з фіктивних робіт нульовою тривалістю) до 1 (для робіт критичного шляху). Чим ближче до 1 коефіцієнт напруженості K(i,j), тим складніше виконати дану роботу у встановлені терміни. Чим ближче K(i,j) до нуля, тим більшим відносним резервом володіє максимальний шлях, що проходить через дану роботу.
Обчислені коефіцієнти напруженості дозволяють додатково класифікувати роботи по зонах. В залежності від величини Кн виділяють три зони: критичну (Кн> 0,8); підкритичну (0,6 <Кн <0,8); резервну (Кн <0,6).
Розрахуємо коефіцієнт напруженості терміну виконання роботи (i,j) та відобразимо в таблиці 4.10.
Таблиця 4.10 – Результати розрахунку коефіцієнтів напруженості
|
Повні шляхи |
t(L) |
Rt(L) |
K(i,j) |
|
L1(1;2;6;8;10;13;14) |
41 |
8 |
0,778 |
|
L2(1;3;5;9;11;14) |
29 |
20 |
0,444 |
|
L3(1;3;5;6;7;12;14) |
35 |
14 |
0,533 |
|
L4(1;3;5;9;12;14) |
28 |
21 |
0,488 |
|
L5(1;4;6;7;12;14) |
24 |
25 |
0,419 |
|
L6(1;4;8;10;13;14) |
26 |
23 |
0,477 |
|
L7(1;3;5;6;10;12;14) |
30 |
19 |
0,472 |
|
L8(1;3;5;6;9;11;14) |
29 |
20 |
0,355 |
|
L9(1;4;6;10;12;13;14) |
19 |
30 |
0,268 |
|
L10(1;4;6;10;12;14) |
19 |
30 |
0,388 |
Розраховуючи коефіцієнти напруженості ми виявили, що співпадання робіт та їх термінів повних шляхів з роботами та термінами робіт критичного шляху становило: для L1 два співпадання термінів робіт, для L2 два співпадання, для L3 три співпадання, для L4 - одне, для L5 - одне, для L6 - одне, для L7 - два, для L8 - три, для L9 - два, для L10 - нуль.
Отже, за проведенними розрахунками можемо зробити висновок, що всі коефіцієнти напруженості, окрім коефіцієнта напруженості критичного шляху, попадають в резервну зону, оскільки K(i,j)<0,6.
Коефіцієнт напруженості повного шляху L10 дорівнює одиниці, це означає, що цей шлях є критичним. Відповідно найменші коефіцієнти напруженості мають повні шляхи L3 та L7.




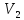













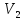



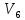










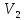













 1
1 4
4
 7
7 12
12