
КР ІЗДН _(Кадастр) / КР 3
.docКОНТРОЛЬНА РОБОТА №3
Для виконання контрольної роботи потрібно:
-
переписати умови всіх задач даного варіанту;
-
опрацювати відповідний теоретичний матеріал посібника;
-
застосувати необхідні формули і розв’язати завдання.
Наведемо зразок контрольної роботи № 4, її виконання і оформлення.
Зразок розв’язання і оформлення контрольної роботи №4
Варіант № 31
Завдання 3.1. Обчислити подвійний інтеграл і перевірити отриманий результат, змінивши порядок інтегрування.
Обчислити
подвійний інтеграл
![]() ,
якщо область D обмежена прямими x=2 , y=x
і гіперболою ху=1. Перевірити отриманий
результат.
,
якщо область D обмежена прямими x=2 , y=x
і гіперболою ху=1. Перевірити отриманий
результат.
Розв’язання. Зобразимо задану область D на рис. 5.3.

рис. 5.3
Оскільки гіпербола ху=1 перетинається з прямою у=х в точці (1; 1), а з прямою х=2 в точці (2; 0,5), то

Перевіримо отриманий результат змінивши межі інтегрування


![]()
Відповідь:
![]()
Завдання
3.2.
Обчислити потрійний інтеграл по області
![]() ,
обмеженій вказаними поверхнями:
,
обмеженій вказаними поверхнями:
Обчислити
![]() ,
якщо область
,
якщо область
![]() обмежена циліндром
обмежена циліндром
![]() і площинами
і площинами
![]() .
.
Розв`язання. Перейдемо до циліндричних координат. Тоді рівняння циліндра набуде вигляду
![]() ,
або
,
або
![]() ,
,
тобто
![]() .
Отже, в області
.
Отже, в області
![]() координати
координати
![]() змінюються таким чином:
змінюються таким чином:
![]() .
Тому,
.
Тому,

![]()
Перехід
від декартових координат
![]() до сферичних
до сферичних
![]() ,
,
пов`язаних
з
![]() співвідношеннями
співвідношеннями
![]()
![]() (
(![]() ,
,
![]() ,
,
![]() ),
здійснюється за формулою
),
здійснюється за формулою
![]()
 .
(5.19)
.
(5.19)
Приклад.
Обчислити
![]() ,
якщо
,
якщо
![]() - куля
- куля
![]() .
.
Розв`язання.
Перейдемо до сферичних координат. В
області
![]() координати
координати
![]() і
і
![]() змінюються так:
змінюються так:
![]() .
Отже,
.
Отже,
![]()
![]() .
.
Завдання 3.3.31. Обчислити криволінійний інтеграл першого роду
![]() де L
відрізок прямої від точки А(0;
0) до точки В(4;
3).
де L
відрізок прямої від точки А(0;
0) до точки В(4;
3).
Розв`язання.
Рівняння прямої АВ має вигляд
![]() Знаходимо
Знаходимо
![]() .
Отже,
.
Отже,![]()
Завдання 4.4.31. Дослідити на збіжність ряди з додатними членами:
а)
![]() ;
б)
;
б)
![]() в)
в)
![]() г)
г)
![]() .
.![]()
Розв’язання.
а) Застосуємо для визначення збіжності
або розбіжності ряду з додатними членами
![]() ознаку порівняння рядів.
ознаку порівняння рядів.
Для
цього порівняємо заданий ряд із рядом
Діріхле
![]() .
.
Перші
члени заданого ряду
![]() :
:
![]() ,
а ряду Діріхле
,
а ряду Діріхле
![]() :
:
![]() .
.
Очевидно,
що при будь-якому
![]() члени ряду Діріхле більше
відповідних членів заданого ряду:
члени ряду Діріхле більше
відповідних членів заданого ряду:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() .
.
Оскільки
ряд
![]() збіжний
збіжний
![]() ,
то за ознакою порівняння рядів заданий
ряд
,
то за ознакою порівняння рядів заданий
ряд
![]() також буде збіжний.
також буде збіжний.
б) Для
перевірки збіжності або розбіжності
ряду
![]() застосуємо ознаку Даламбера. Для цього
запишемо
застосуємо ознаку Даламбера. Для цього
запишемо
![]() -й
і (
-й
і (![]() )-й
члени ряду:
)-й
члени ряду:
![]() .
.
Знайдемо границю відношення за формулою (6.7)
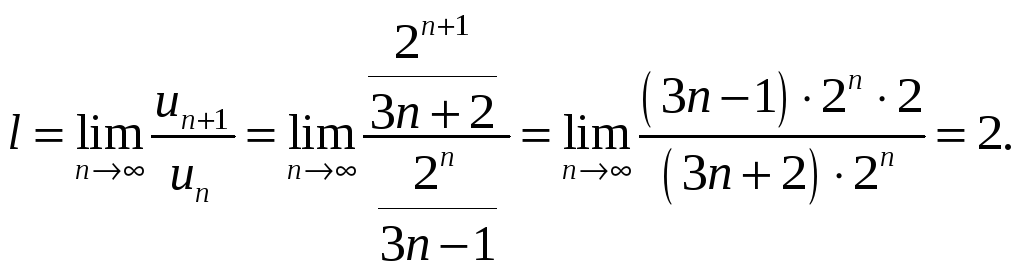
Оскільки
границя відношення
![]() ,
то за ознакою Даламбера ряд
,
то за ознакою Даламбера ряд
![]() розбіжний.
розбіжний.
в) До
ряду
![]() застосуємо радикальну ознаку Коші. За
формулою (6.8) маємо:
застосуємо радикальну ознаку Коші. За
формулою (6.8) маємо:

Оскільки
![]() ,
то згідно з радикальною ознакою Коші
ряд
,
то згідно з радикальною ознакою Коші
ряд
![]() розбіжний.
розбіжний.
г) До
ряду
![]() застосуємо інтегральну ознаку Коші.
Для цього розглянемо загальний член
ряду
застосуємо інтегральну ознаку Коші.
Для цього розглянемо загальний член
ряду
![]() і побудуємо функцію
і побудуємо функцію
![]() .
.
Обчислимо невласний інтеграл:

![]()
![]() .
.
Таким
чином, невласний інтеграл
![]() збіжний і згідно з інтегральною ознакою
Коші збіжний і ряд
збіжний і згідно з інтегральною ознакою
Коші збіжний і ряд
![]() .
.
Завдання 4.4.5.. Дослідити на збіжність ряди:
a)
![]() ;
б)
;
б)
![]() .
.
Розв’язання. а) Заданий ряд є знакозмінним. Побудуємо ряд із абсолютних величин членів заданого ряду:
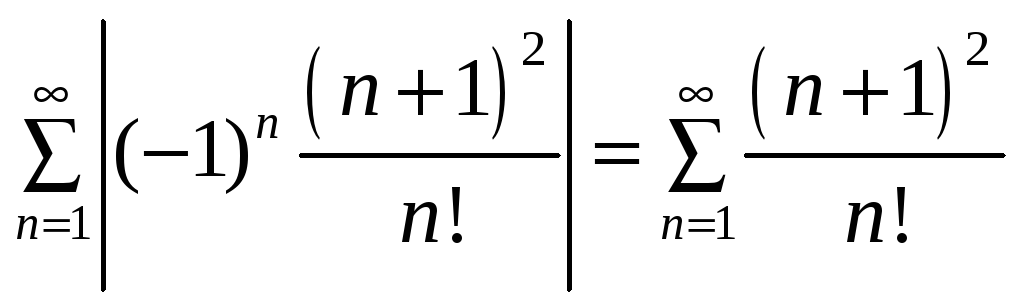 .
.
Отримали ряд з додатними членами і для визначення його збіжності або розбіжності застосуємо ознаку Даламбера. Для цього запишемо
![]()
і за формулою (6.7) обчислимо границю відношення

![]()
Оскільки
![]() ,
то за ознакою Даламбера ряд з абсолютних
величин елементів заданого ряду збіжний
і за означенням ряд
,
то за ознакою Даламбера ряд з абсолютних
величин елементів заданого ряду збіжний
і за означенням ряд
![]() збіжний абсолютно.
збіжний абсолютно.
б) Заданий ряд є знакозмінним Побудуємо ряд із абсолютних величин членів заданого ряду:
![]() .
.
Отримали
ряд з додатними членами і для визначення
його збіжності або розбіжності застосуємо
інтегральну ознаку Коші. Запишемо
функцію
![]() і обчислимо невласний інтеграл
і обчислимо невласний інтеграл
![]()
![]()
![]() .
.
Невласний
інтеграл
![]() збіжний і згідно з інтегральною ознакою
Коші збіжний і ряд
збіжний і згідно з інтегральною ознакою
Коші збіжний і ряд
![]() .
.
Отже,
заданий ряд
![]() збіжний абсолютно.
збіжний абсолютно.
Завдання 4.6.31. Знайти радіус, інтервал і область збіжності степеневих рядів:
а)
![]() ;
б)
;
б)
![]() .
.
Розв’язання. а) Радіус збіжності знайдемо за формулою (6.16):
![]() ,
,
![]() ,
,

![]() .
.
Радіус
збіжності степеневого ряду дорівнює
![]() ,
а інтервал збіжності
,
а інтервал збіжності
![]() .
.
Для
отримання області збіжності степеневого
ряду дослідити збіжність ряду на кінцях
інтервалу збіжності в точках
![]() ,
,![]() .
.
При
![]() степеневий ряд перетворюється в
знакопочережний числовий ряд
степеневий ряд перетворюється в
знакопочережний числовий ряд
![]() ,
,
в якому його члени, монотонно спадаючи, прямують до нуля
![]() ,
,
![]()
Отже,
за ознакою Лейбніца ряд збігається і
точку
![]() додамо до області збіжності.
додамо до області збіжності.
При
![]() степеневий ряд перетворюється в
знакододатний числовий ряд
степеневий ряд перетворюється в
знакододатний числовий ряд
![]() .
.
Для
будь-яких значень
![]() виконується нерівність
виконується нерівність
![]() .
.
За
ознакою порівняння рядів ряд
![]() збіжний, оскільки збіжний ряд
збіжний, оскільки збіжний ряд
![]() з більшими членами (як ряд Діріхле, де
з більшими членами (як ряд Діріхле, де
![]() ).
Таким чином, точка
).
Таким чином, точка
![]() належить області збіжності.
належить області збіжності.
Отже,
областю збіжності степеневого ряду
![]() є відрізок
є відрізок
![]() .
.
б)
Обчислюємо радіус збіжності степеневого
ряду
![]() за формулою (6.16):
за формулою (6.16):
![]() ;
;
![]() ;
;
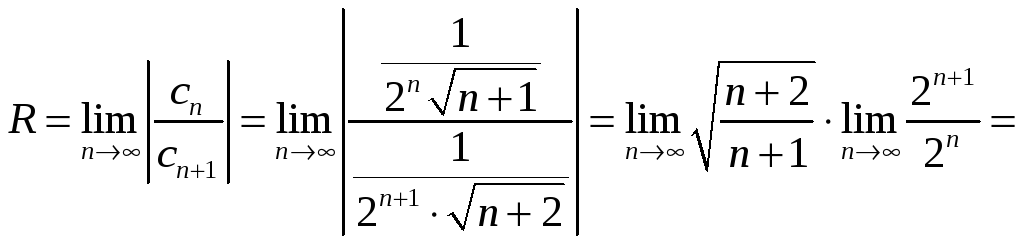
![]() .
.
Радіус
збіжності
![]() ,
а інтервал збіжності
,
а інтервал збіжності
![]() .
.
Дослідимо
поведінку степеневого ряду на кінцях
інтервалу збіжності в точках
![]() ,
,
![]() .
.
При
![]() маємо знакододатний числовий ряд
маємо знакододатний числовий ряд
![]() .
.
Порівняємо
його з рядом Діріхле
![]() (
(![]() ),
який є розбіжним, а це означає, що і
досліджуваний ряд розбіжний. Отже, точка
),
який є розбіжним, а це означає, що і
досліджуваний ряд розбіжний. Отже, точка
![]() не належить області збіжності.
не належить області збіжності.
При
![]() маємо знакопочережний числовий ряд
маємо знакопочережний числовий ряд
![]() ,
,
який задовольняє умовам ознаки Лейбніца:
![]() ,
,
![]() ,
,
тому є
збіжним і точка
![]() належить області збіжності.
належить області збіжності.
Отже,
областю збіжності степеневого ряду
![]() є півінтервал
є півінтервал
![]() .
.
Завдання 4.7.31. Розкласти в ряд Маклорена функцію
![]() .
.
Розв’язання. Застосуємо розкладання в ряд Маклорена (6.19) функції
![]() .
.
Нехай
![]() .
Тоді
.
Тоді
![]() ,
або
,
або
![]() .
.
Отже,
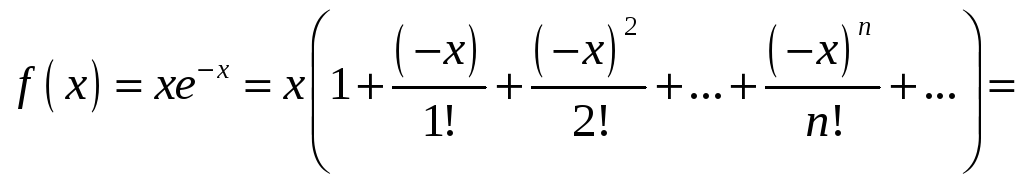
![]() .
.
Маємо
розклад функції
![]() в ряд Маклорена:
в ряд Маклорена:
![]() .
.
Ряд
в правій частині рівності має областю
збіжності всю числову вісь
![]() і його сумою є функція.
і його сумою є функція.
3.1. Обчислити подвійний інтеграл і перевірити отриманий результат, змінивши порядок інтегрування. Тут область D обмежена вказаними лініями.
3.1.1 ![]() .
.
3.1.2 ![]() .
.
3.1.3 ![]() .
.
3.1.4 ![]() .
.
3.1.5 ![]() .
.
3.1.6 ![]() .
.
3.1.7 ![]() .
.
3.1.8 ![]() .
.
3.1.9 ![]() .
.
3.1.10 ![]() .
.
3.1.11 ![]() .
.
3.1.12 ![]() .
.
3.1.13 ![]() .
.
3.1.14 ![]() .
.
3.1.15 ![]() .
.
3.1.16 ![]() .
.
3.1.17 ![]() .
.
3.1.18 ![]() .
.
3.1.19 ![]() .
.
3.1.20 ![]() .
.
3.1.21 ![]() .
.
3.1.22 ![]() .
.
3.1.23 ![]() .
.
3.1.24 ![]() .
.
3.1.25 ![]() .
.
3.1.26 ![]() .
.
3.1.27 ![]() .
.
3.1.28 ![]() .
.
3.1.29 ![]() .
.
3.1.30 ![]() .
.
Завдання 3.2
Обчислити
потрійний інтеграл по області
![]() ,
обмеженій вказаними поверхнями:
,
обмеженій вказаними поверхнями:
3.2.1![]()
3.2.2![]()
3.2.3![]()
3.2.4![]()
3.2.5![]()
3.2.6
![]()
3.2.7
![]()
3.2.8
![]()
3.2.9
![]()
3.2.10![]()
3.2.11![]()
3.2.12![]()
3.2.13![]()
3.2.14![]()
3.2.15![]()
3.2.16![]()
3.2.17
![]()
3.2.18
![]()
3.2.19![]()
3.2.20![]()
3.2.21![]()
3.2.22![]()
3.2.23![]()
3.2.24![]()
3.2.25![]()
3.2.26![]()
3.2.27
![]()
3.2.28![]()
3.2.29![]()
3.2.30![]()
Завдання 3.3. Обчислити криволінійний інтеграл першого роду.
3.3.1.
![]() ,
L - відрізок
прямої
,
L - відрізок
прямої
![]() між
точками
між
точками
![]() ,
,
![]() .
.
3.3.2.
![]() ;
L - дуга
кривої
;
L - дуга
кривої
![]() між
точками
між
точками
![]() та
та
![]() .
.
3.3.3.
![]() ;
L - дуга
кривої
;
L - дуга
кривої
![]() між точками
між точками
![]() ;
;
![]() .
.
3.3.4.
![]() ;
L - дуга
кривої
;
L - дуга
кривої
![]() між точками
між точками
![]() ;
;
![]() .
.
3.3.5.
![]() ;
L - дуга
кривої
;
L - дуга
кривої
![]() між точками
між точками
![]() ;
;
![]() .
.
3.3.6.![]() ;
L - дуга
синусоїди
;
L - дуга
синусоїди
![]() ,
,
![]() .
.
3.3.7.
![]() ;
L - дуга
косинусоїди
;
L - дуга
косинусоїди
![]() ,
,
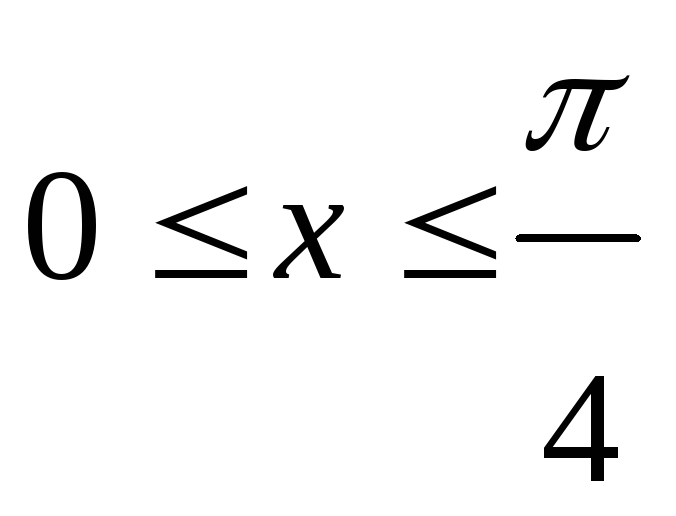 .
.
3.3.8.
![]() ;
L - дуга
тангенсоїди
;
L - дуга
тангенсоїди
![]() ,
,
![]()
3.3.9.
![]() L
- дуга кривої
L
- дуга кривої
![]() ,
,
![]() .
.
3.3.10.
![]() ;L
- дуга кривої
;L
- дуга кривої
![]() ,
,
![]()
3.3.11.
![]() ;
L - верхне
півколо
;
L - верхне
півколо
![]()
![]()
3.3.12.
![]() ;
L - дуга
кривої
;
L - дуга
кривої
![]() ,
,
![]() ,
,
![]() ,
,
![]()
3.3.13.
![]() ;
L - арка
циклоїди
;
L - арка
циклоїди
![]() ,
,
![]() ,
,
![]() .
.
3.3.14.
![]() ;
L - дуга
кривої
;
L - дуга
кривої
![]()
![]()
![]()
3.3.15
![]() ;
L - дуга
кривої
;
L - дуга
кривої
![]() ,
,
![]() ,
,
![]() .
.
3.3.16
![]() ;
L - коло
;
L - коло
![]()
Обчислити довжину дуги вказаної кривої.
3.3.17.
![]() ,
,
![]()
![]()
![]()
