
Контрольна робота № 1
Для виконання контрольної роботи потрібно:
1) переписати умови всіх задач даного варіанту (можна замість повних умов задач записати лише їх номер);
опрацювати відповідний теоретичний матеріал посібника;
застосувати необхідні формули і розв’язати завдання.
Наведемо зразок контрольної роботи № 1, її виконання і оформлення.
Зразок розв’язання і оформлення контрольної роботи № 1.
Варіант№31
Завдання
1.1.31
Знайти матрицю![]() ,
,
якщо
![]() ;
;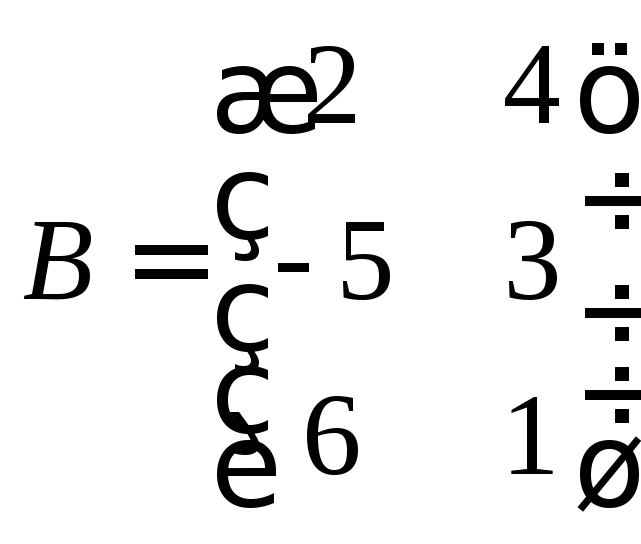 ;
;![]() .
.
Розв’язання.
Знайдемо добуток матриць ![]() і
і ![]() :
:
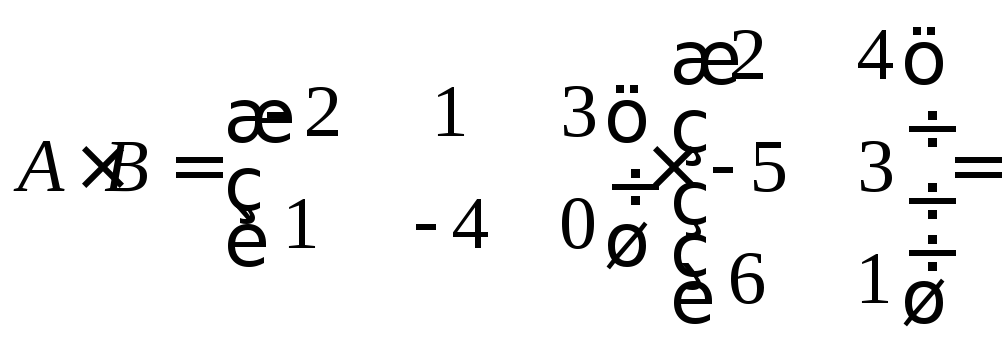
![]()
Помножимо
знайдену матрицю
![]() на 4:
на 4:
![]()
Піднесемо
матрицю
![]() до квадрата і помножимо її на 3:
до квадрата і помножимо її на 3:
![]()
Знайдемо матрицю
![]() :
:
![]()
Завдання 1.2.31Дослідити на сумісність і розв’язати систему лінійних рівнянь, користуючись методом Гаусса, Крамера та матричним
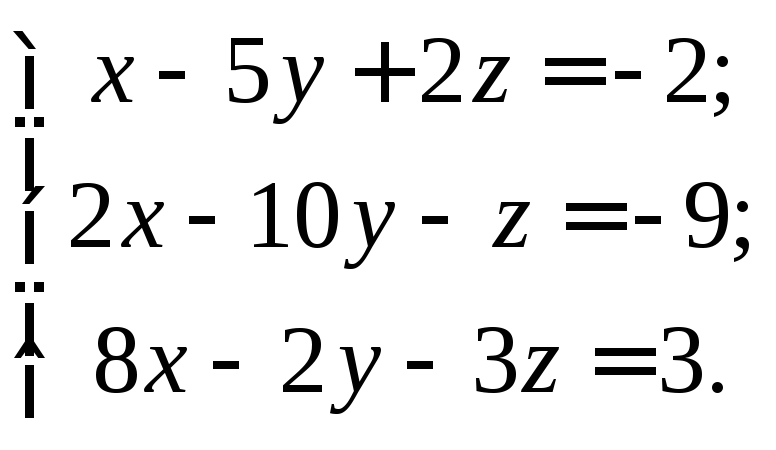
Розв’язання.
Дослідимо систему рівнянь на
сумісність за допомогою теореми
Кронекера-Капеллі. Запишемо розширену
матрицю![]() системи:
системи:
 .
.
Виконаємо
елементарні перетворення матриці
![]() ,
а саме: помножимо елементи першого
рядка на (
,
а саме: помножимо елементи першого
рядка на (![]() 2)
і додамо до другого; помножимо
елементи першого рядка на (
2)
і додамо до другого; помножимо
елементи першого рядка на (![]() 8)
і додамо до третього рядка.
Отримаємо
8)
і додамо до третього рядка.
Отримаємо
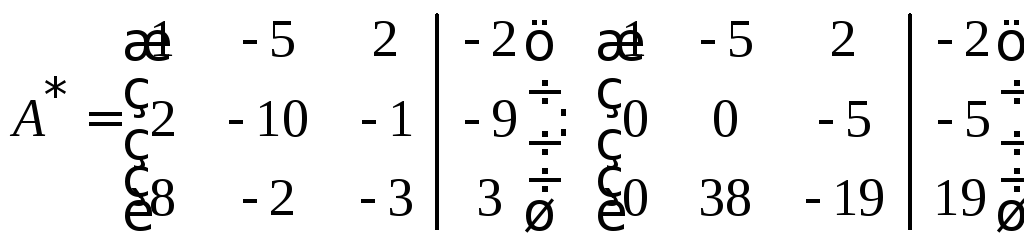 .
.
Оскільки
![]() і кількість невідомих
і кількість невідомих ![]() ,
то система сумісна і має єдиний розв’язок.
,
то система сумісна і має єдиний розв’язок.
Відповідно до останньої матриці, система набула трикутного вигляду:
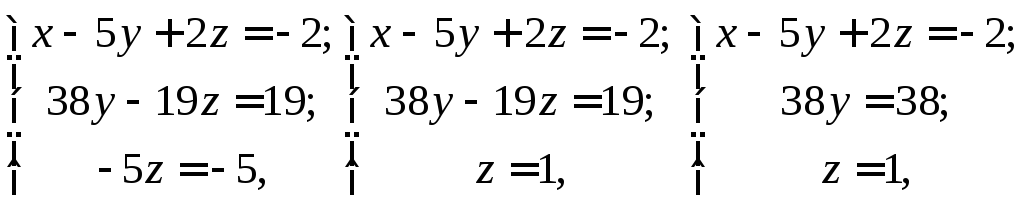
![]()
Отже, розв’язком
системи є:
![]()
Розв’яжемо систему рівнянь методом Крамера.
Знайдемо
визначник системи рівнянь![]() та визначники
та визначники![]() ,
,![]() ,
,![]() :
:
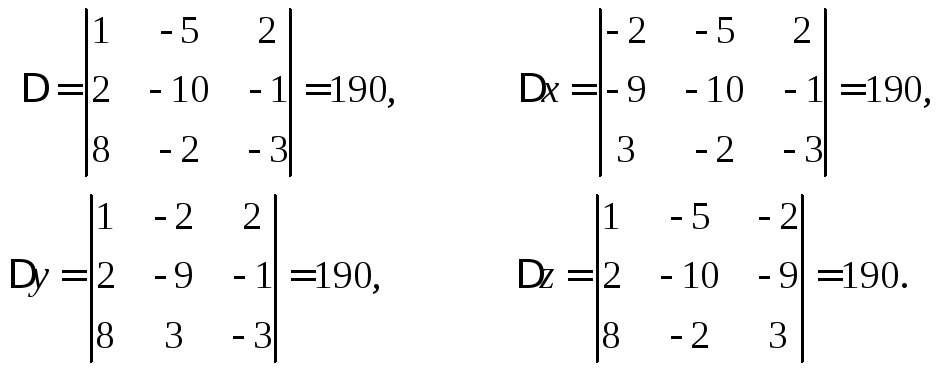
Оскільки
![]() ,
то система рівнянь має єдиний розв’язок,
який знайдемо за формулами Крамера
(1.15):
,
то система рівнянь має єдиний розв’язок,
який знайдемо за формулами Крамера
(1.15):
![]()
Отже, розв’язком
системи є:
![]() Дійсно, підставивши отриманий розв’язок
в задану систему рівнянь, отримаємо
тотожності.
Дійсно, підставивши отриманий розв’язок
в задану систему рівнянь, отримаємо
тотожності.
Розв’яжемо систему рівнянь матричним методом.
Запишемо
матриці
![]() та
та![]() системи у вигляді:
системи у вигляді:
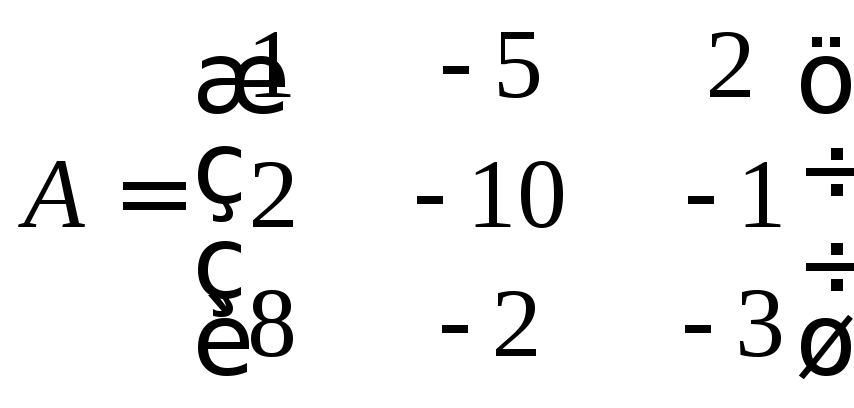 ;
;
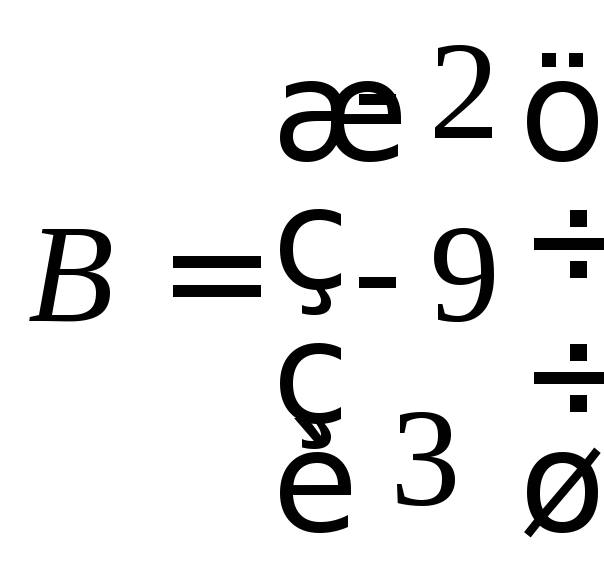 ;
;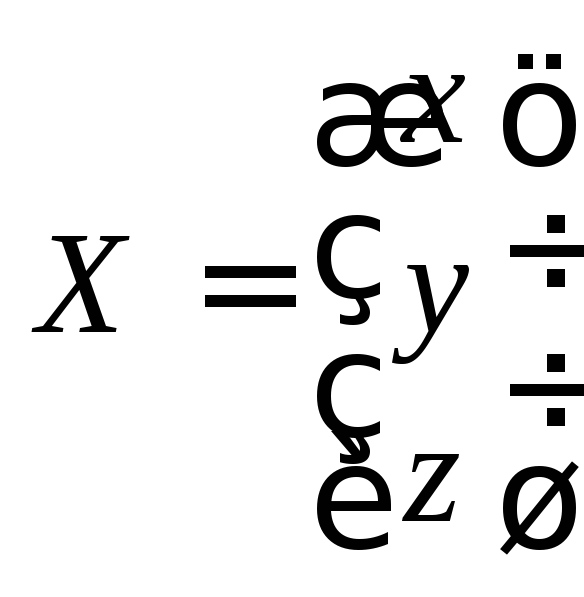 .
.
Згідно
з формулою (1.16) систему лінійних рівнянь
можна записати матричним рівнянням
![]() розв’язок
якого задається формулою (1.17).
розв’язок
якого задається формулою (1.17).
Знайдемо
матрицю, обернену до матриці
![]() ,
за формулою (1.6). Для цього спочатку
обчислимо визначник матриці
,
за формулою (1.6). Для цього спочатку
обчислимо визначник матриці![]() :
:
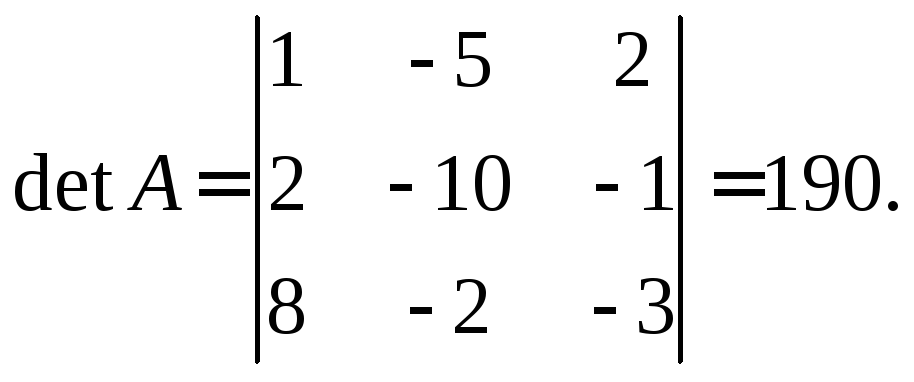
Оскільки
![]() то обернена матриця існує. Обчислимо
алгебраїчні доповнення елементів
матриці
то обернена матриця існує. Обчислимо
алгебраїчні доповнення елементів
матриці![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Отже, обернена матриця має вигляд:
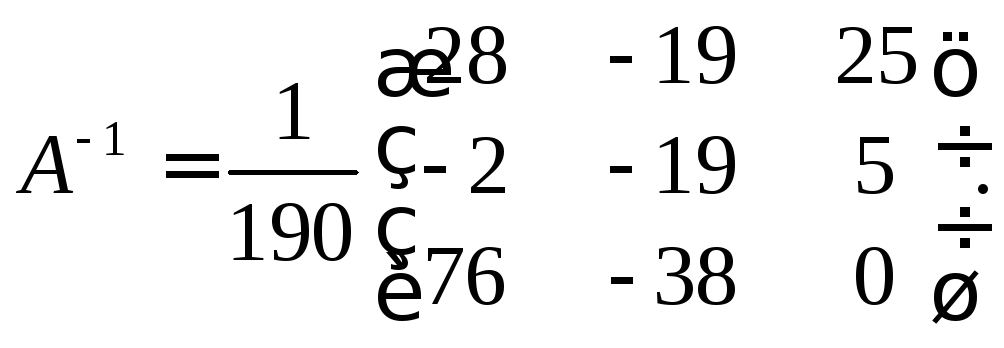
Знайдемо
матрицю
![]() як добуток двох матриць
як добуток двох матриць![]() і
і![]() :
:
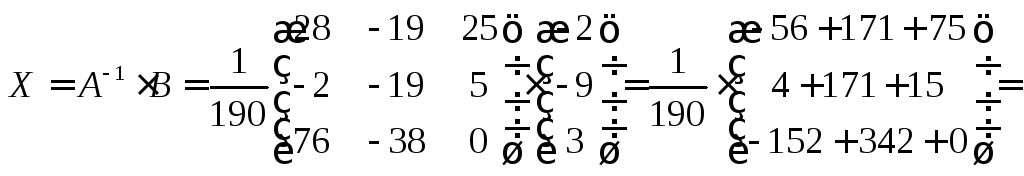
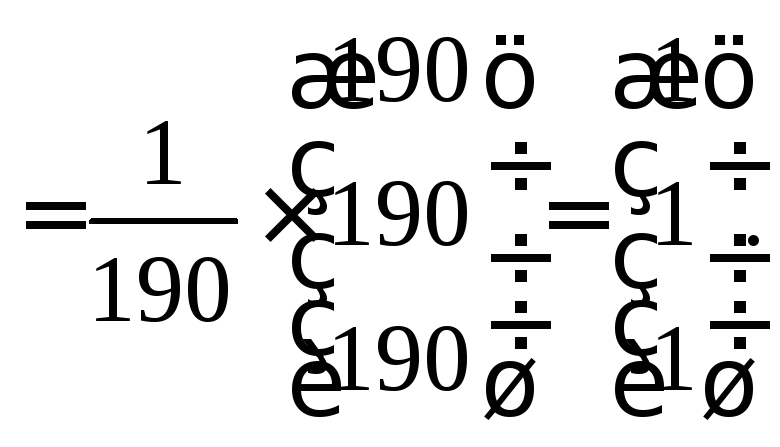
Таким
чином,
![]()
Завдання 1.3.31
Задані
координати точок
![]()
![]()
![]() ,
,![]() - вершини піраміди
- вершини піраміди![]() Знайти:
Знайти:
а)
координати векторів
![]() ,
,![]() ,
,![]() та їхні довжини;
та їхні довжини;
б) кут
при вершині
![]() грані
грані
![]() ;
;
в) площу
основи
![]() піраміди
піраміди![]() ;
;
г) об’єм
піраміди
![]() та довжину висоти
та довжину висоти![]() ,
опущеної з вершини
,
опущеної з вершини![]() на основу
на основу![]() .
.
Розв’язання.
а)
Знайдемо координати векторів
![]() ,
,![]() ,
,![]() ,
застосувавши формулу (2.5):
,
застосувавши формулу (2.5):
![]()
![]()
![]()
Для знаходження довжини вектора застосуємо формулу (2.4):
![]()
![]()
![]()
б) З
формули (2.17) знайдемо
![]() :
:
 .
.
За
формулою (2.19) знайдемо:
![]() .
.
Кут при
вершині
![]() грані
грані
![]() :
:![]()
в) Якщо
відомі координати вершин трикутника
![]() ,
то його площу можна знайти за формулою
,
то його площу можна знайти за формулою
![]() .
.
![]()
![]() ,
,
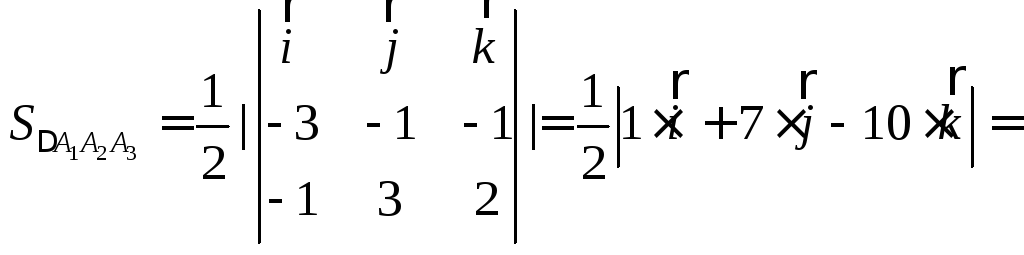
![]() .
.
Отже,
площа основи
![]() піраміди
піраміди![]() дорівнює
дорівнює![]() .
.
г)
Використаємо формулу (2.26) для знаходження
об’єму піраміди
![]() :
:
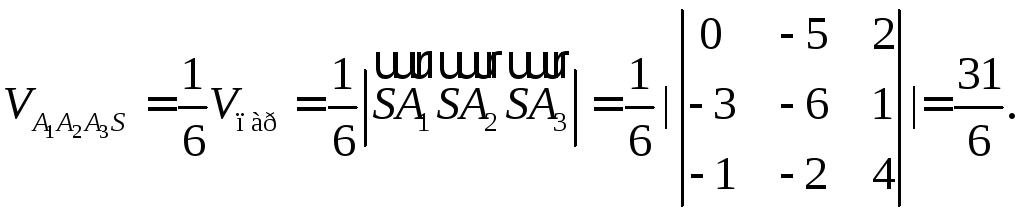
З формули
об’єму піраміди
![]() виразимо
виразимо
![]() ,
,
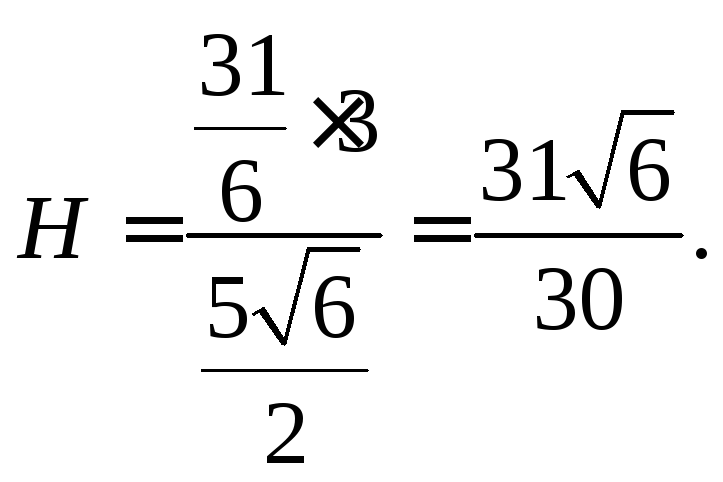
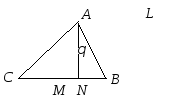
Завдання 1.4..31Задано трикутник
![]() з вершинами
з вершинами![]()
![]()
![]() .
Необхідно:
.
Необхідно:
а) скласти
рівняння сторони
![]() ,
записати у відрізках на осях та у вигляді
рівняння з кутовим коефіцієнтом, привести
до нормального виду;
,
записати у відрізках на осях та у вигляді
рівняння з кутовим коефіцієнтом, привести
до нормального виду;
б)
записати загальне рівняння медіани
![]() ,
висоти
,
висоти![]() та прямої
та прямої![]() ,
яка паралельна стороні
,
яка паралельна стороні![]() ;
;
в) знайти
довжину висоти
![]() та внутрішній кут між медіаною
та внутрішній кут між медіаною![]() і стороною
і стороною![]() .
.
Розв’язання:
а) рівняння сторони
![]() знайдемо за формулою (3.5)
знайдемо за формулою (3.5)
і приведемо його до вигляду рівняння з кутовим коефіцієнтом:
![]()
![]()
![]()
Зведемо рівняння
сторони
![]() до вигляду рівняння прямої у відрізках
на осях (3.11), де
до вигляду рівняння прямої у відрізках
на осях (3.11), де![]() і
і![]()
![]() ,
а отже,
,
а отже,
![]() ,
,![]()
Підставивши у
рівняння
![]() замість
замість![]() і
і![]() їх числові значення, отримаємо:
їх числові значення, отримаємо:
![]()
Загальне рівняння
прямої
![]() :
:![]() приведемо до нормального виду. Обидві
частини загального рівняння необхідно
помножити на нормуючий множник
приведемо до нормального виду. Обидві
частини загального рівняння необхідно
помножити на нормуючий множник![]() .
В даному випадку
.
В даному випадку![]() Знак нормуючого множника береться
протилежним знаку вільного члена
загального рівняння. Отже,
Знак нормуючого множника береться
протилежним знаку вільного члена
загального рівняння. Отже,
![]()
Помножимо дане
рівняння на
![]() і отримаємо нормальне рівняння прямої
і отримаємо нормальне рівняння прямої![]() :
:
![]()
б) знайдемо точку М, як середину сторони ВС.
![]() .
.
Складемо рівняння
медіани
![]() ,
як рівняння прямої, що проходять через
дві точки, використовуючи формулу (3.5):
,
як рівняння прямої, що проходять через
дві точки, використовуючи формулу (3.5):
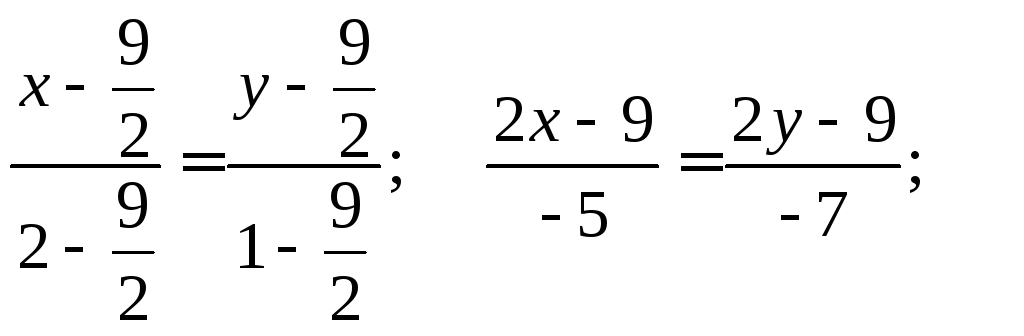
![]()
![]() ;
;
![]() .
.
Знайдемо рівняння
висоти
![]() за формулою (3.10). Оскільки висота
за формулою (3.10). Оскільки висота![]() проходить через точку
проходить через точку![]() і має нормальний вектор
і має нормальний вектор![]() ,
то рівняння висоти має вигляд:
,
то рівняння висоти має вигляд:
![]() ,
,
![]() .
.
Напрямний вектор
прямої
![]()
![]() .
Оскільки пряма
.
Оскільки пряма![]() паралельна стороні
паралельна стороні![]() ,
і враховуючи, що пряма
,
і враховуючи, що пряма![]() проходить через точку
проходить через точку![]() ,
за формулою (3.6) запишемо шукане рівняння
прямої
,
за формулою (3.6) запишемо шукане рівняння
прямої![]() :
:
![]() .
.
в) довжину
висоти
![]() знаходимо як відстань
знаходимо як відстань![]() від точки
від точки![]() до сторони
до сторони![]() за формулою (3.22):
за формулою (3.22):
![]()
Запишемо рівняння
прямої
![]() як рівняння прямої, що проходять через
дві точки, використовуючи формулу (3.5)
і приведемо його до загального вигляду:
як рівняння прямої, що проходять через
дві точки, використовуючи формулу (3.5)
і приведемо його до загального вигляду:
![]()
![]()
![]() .
.
Кут між медіаною
![]() і
стороною
і
стороною![]() знайдемо за формулою (3.13). Для цього
визначимо кутові коефіцієнти прямих
знайдемо за формулою (3.13). Для цього
визначимо кутові коефіцієнти прямих![]() і
і![]() :
:
![]() ,
,
![]() .
.
 ,
,
![]() .
.
Завдання 1.5.31. Обчислити границі, не користуючись правилом Лопіталя:
а)![]() ; б)
; б)
![]() ; в)
; в)![]() ;
;
г)
![]() ; д)
; д)![]() ;
е)
;
е)![]() ; є)
; є)![]() .
.
Розв’язання:
а)
розкладемо чисельник і знаменник дробу
на множники, а потім скоротимо дріб на
![]() :
:![]()
![]()
б)
помножимо чисельник і знаменник дробу
на вираз
![]() ,
а потім скоротимо дріб на
,
а потім скоротимо дріб на![]() :
:
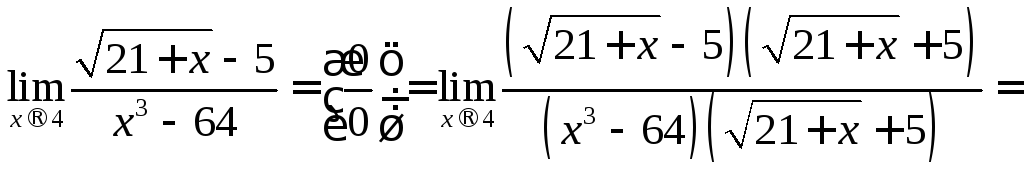
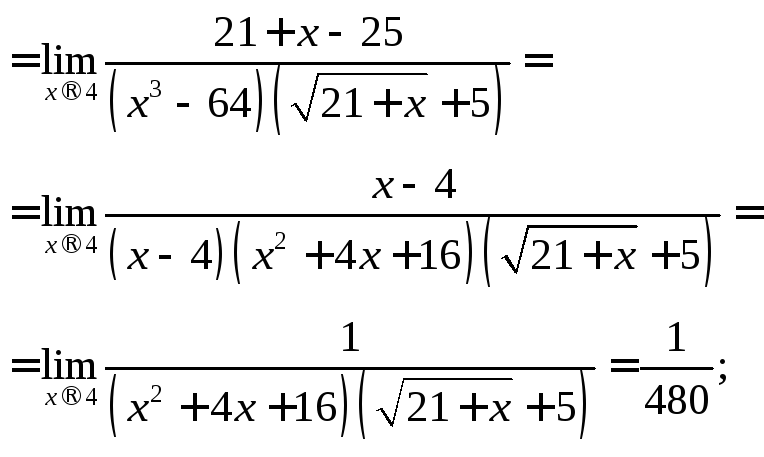
в)
користуючись таблицею еквівалентних
нескінченно малих величин, замінимо
нескінченно малі величини в чисельнику
і знаменнику еквівалентними:
![]() ;
;
г) скористаємось другою важливою границею(4.2):
![]()
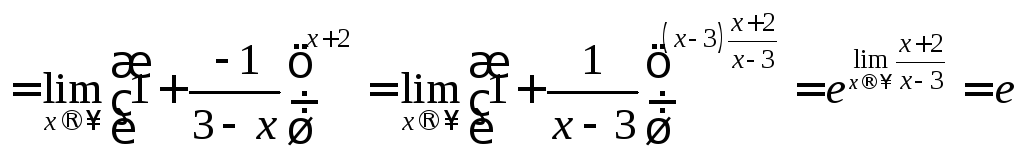 ;
;
д)
поділимо чисельник і знаменник дробу
на
![]() в найбільшому степені, тобто на
в найбільшому степені, тобто на![]() :
:
![]() ;
;
е)поділимо чисельник і знаменник
дробу на
![]() в найбільшому степені, тобто на
в найбільшому степені, тобто на![]() :
:
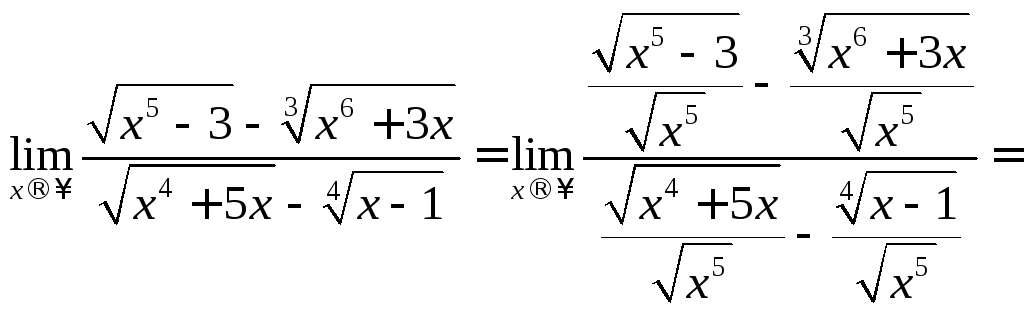

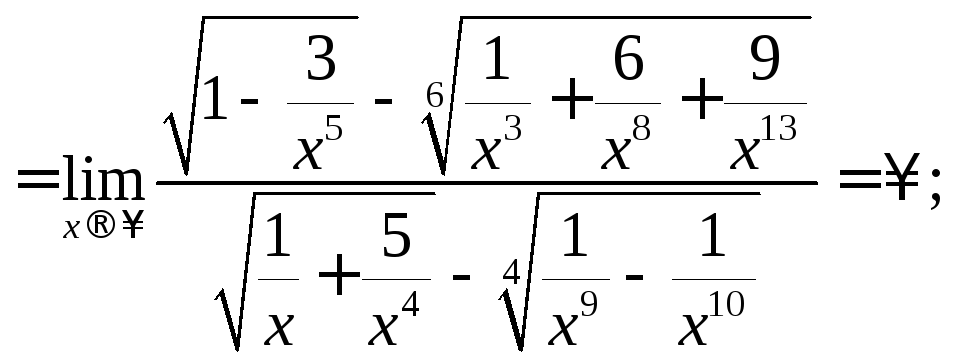
є)
помножимо чисельник і знаменник дробу
на вираз
![]() ,
виконаємо тригонометричні перетворення
та замінимо в чисельнику нескінченно
малі величини
,
виконаємо тригонометричні перетворення
та замінимо в чисельнику нескінченно
малі величини![]() і
і![]() еквівалентними, потім скоротимо дріб
на
еквівалентними, потім скоротимо дріб
на![]() :
:
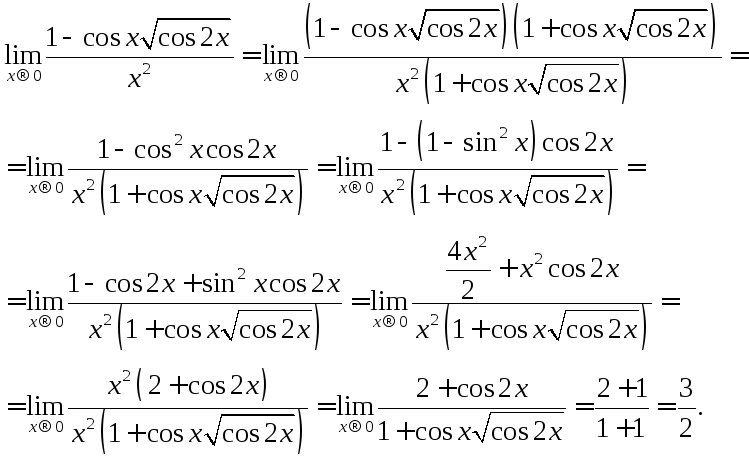
Завдання 1.7.31. Знайти похідні функцій:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)![]() ;
г)
;
г)![]() .
.
Розв’язання:
а)скористаємось правилом диференціювання складеної функції (5.9):
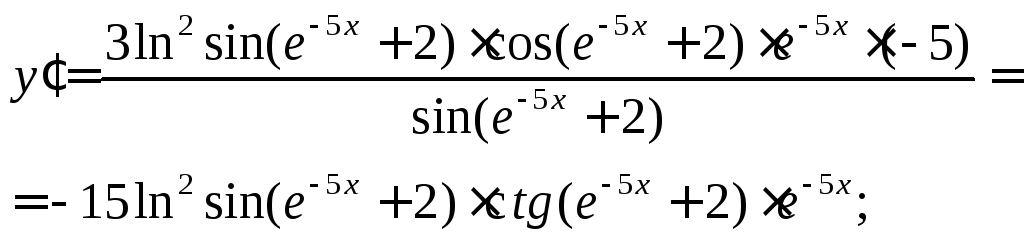
б) скористаємось формулою похідної добутку двох функцій (5.7) та правилом диференціювання складеної функції (5.9):
![]() ;
;
в)
прологарифмуємо обидві частини рівності,
а потім продиференціюємо отриману
рівність, використовуючи правило
диференціювання складеної функції
(5.9):
![]()
![]() ,
звідси:
,
звідси:
![]() ;
;
г)
продиференціюємо обидві частини рівності
по ![]() ,
вважаючи
,
вважаючи
![]() функцією від
функцією від![]() :
:
![]() ;
;![]() ;
;![]() ;
;
![]() .
.
Завдання
1.8..31 Знайти похідну
функції, заданої параметрично: ![]()
Розв’язання.
Знайдемо похідну![]() :
: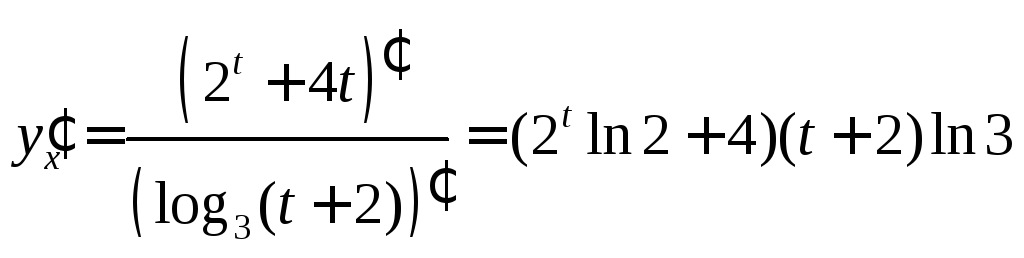 .
.
Завдання
1.9..31 Знайти похідну
другого порядку функції
![]() .
.
Розв’язання.
Знайдемо спочатку похідну першого
порядку даної функції:
![]() ,
потім знайдемо похідну другого порядку:
,
потім знайдемо похідну другого порядку: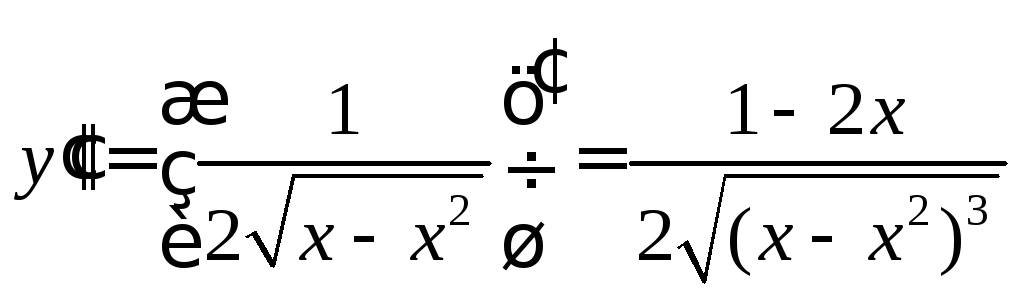 .
.
Завдання
1.10..31 Скласти рівняння
дотичної та нормалі до кривої
![]() в точці з абсцисою
в точці з абсцисою![]() .
.
Розв’язання.
Знайдемо похідну даної функції та її
значення в точці
![]() :
:
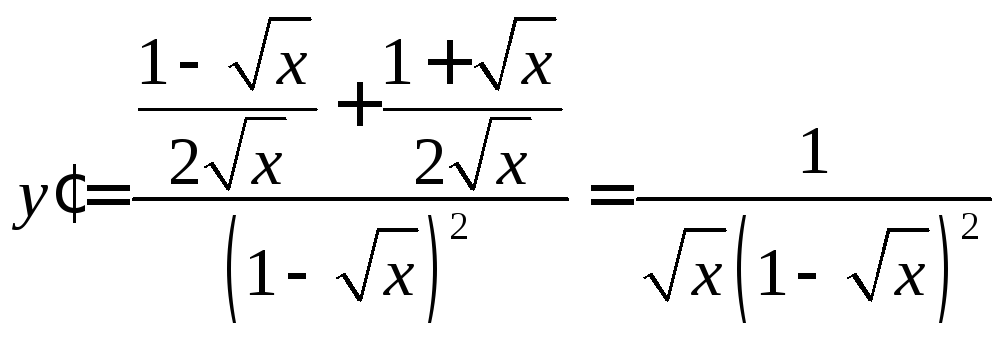 ,
,
 .
.
Знайдемо
![]() :
:![]() .
Підставимо отримані значення в рівняння
дотичної (5.5) та нормалі (5.6):
.
Підставимо отримані значення в рівняння
дотичної (5.5) та нормалі (5.6):
Отже, рівняння дотичної до даної кривої:
![]() або
або
![]() ;
;
рівняння
нормалі:
![]() або
або![]() .
.
Завдання
1.11..31 Знайти диференціал
та наближене значення функції
![]() в
точці
в
точці
![]() .
.
Розв’язання.
Знайдемо диференціал
функції за формулою (5.13):
![]() .
.
Знайдемо
наближене значення функції в точці за
формулою (5.14),
де![]()
![]()
Завдання
1.12..31 Знайти границі за
правилом Лопіталя: а)
![]() ;
б)
;
б)![]() .
.
Розв’язання: а) подамо добуток функцій у вигляді частки, а потім застосуємо правило Лопіталя (5.15):
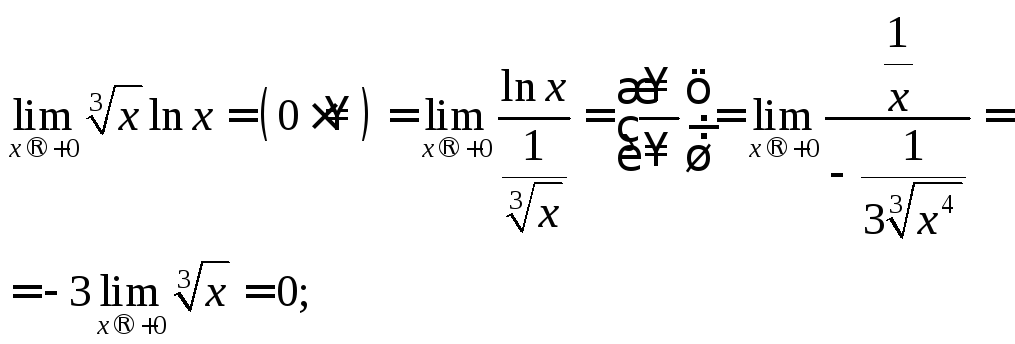
б) запишемо функцію у вигляді степеня з натуральною основою і, користуючись властивістю логарифмів, подамо показник степеня у вигляді частки, що дасть можливість використати правило Лопіталя (5.15):

![]()
Завдання 1.13..31 Дослідити функції та побудувати їх графіки:
а)
![]() ;
б)
;
б) ![]() .
.
Розв’язання:
а) Область визначення даної функції
![]() .
В точці
.
В точці
![]() функція має розрив. Знайдемо односторонні
границі функції:
функція має розрив. Знайдемо односторонні
границі функції:
![]() ,
,
отже,
![]() — точка розриву другого роду.
— точка розриву другого роду.
Пряма
![]() є вертикальною
асимптотою кривої.
є вертикальною
асимптотою кривої.
Функція ні парна, ні непарна, неперіодична.
Знайдемо екстремуми та інтервали монотонності функції:
![]()
![]() в
точці
в
точці
![]() , яка є
критичною,
, яка є
критичною,
![]() не існує
в точці
не існує
в точці
![]() ,
але це не критична точка, тому що вона
є точкою розриву .
,
але це не критична точка, тому що вона
є точкою розриву .
![]() — функція зростає
при
— функція зростає
при
![]()
![]() —функція спадає
при
—функція спадає
при
![]() .Отже,
.Отже,
![]() —
точкамінімуму:
—
точкамінімуму:
![]() .
.
Знайдемо інтервали опуклості та вгнутості, точки перегину:
![]()
![]() ,
,
![]() не існує при
не існує при
![]() ,
але ця точка не може бути точкою перегину,
тому що є точкою розриву.
,
але ця точка не може бути точкою перегину,
тому що є точкою розриву.
Отже,
графік функції не має точок перегину,
причому
![]() на всій області визначення, тому графік
функції всюди вгнутий.
на всій області визначення, тому графік
функції всюди вгнутий.
Знайдемо асимптоти:
![]() —
вертикальна
асимптота;
—
вертикальна
асимптота;
![]()
![]()
отже,
пряма
![]() —
похила асимптота.
—
похила асимптота.
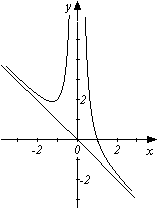
Графік функції перетинає вісь Ox в точці (1;0) і не перетинає вісь Oy.
За результатами досліджень будуємо графік функції:
б) Область
визначення даної функції
![]() .В точці
.В точці
![]() функція має розрив. Використовуючи
правило Лопіталя (5.15), знайдемо односторонні
границі функції:
функція має розрив. Використовуючи
правило Лопіталя (5.15), знайдемо односторонні
границі функції:
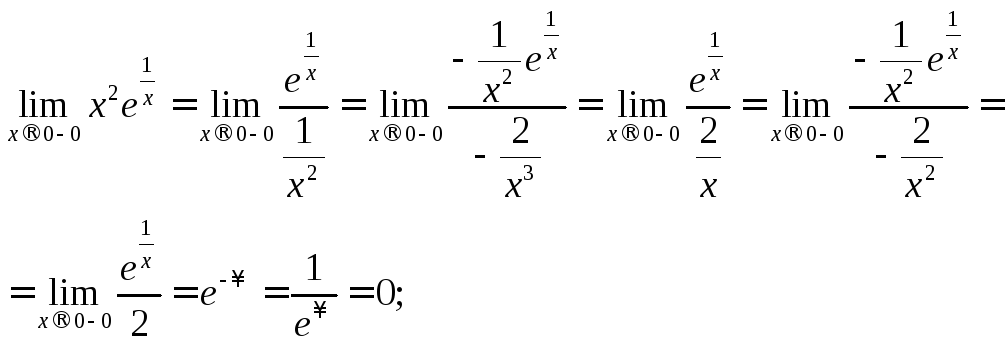
аналогічно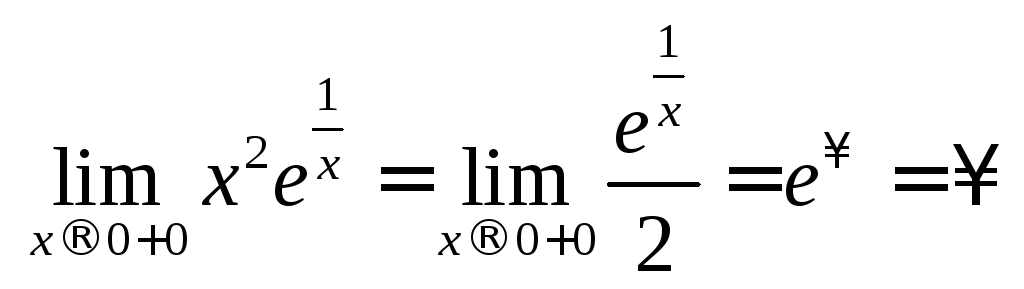 ,
,
отже,
![]() — точка розриву другого роду.
— точка розриву другого роду.
Пряма
![]() є вертикальною
асимптотою кривої.
є вертикальною
асимптотою кривої.
Функція ні парна, ні непарна, неперіодична.
Знайдемо екстремуми та інтервали монотонності функції:
![]() ,
,
![]() в
точці
в
точці
![]() ,
яка є критичною,
,
яка є критичною,
![]() не існує
в точці
не існує
в точці
![]() ,
але це не критична точка, тому що вона
є точкою розриву .
,
але це не критична точка, тому що вона
є точкою розриву .
![]() — функція зростає
при
— функція зростає
при
![]() ,
,
![]() —функція спадає
при
—функція спадає
при
![]() .Отже,
.Отже,
![]() —
точкамінімуму:
—
точкамінімуму:
![]() .
.
Знайдемо інтервали опуклості та вгнутості, точки перегину:
![]() ,
,
![]() ,
,
![]() існує на всій області визначення функції.
Отже, графік функції не має точок
перегину, причому
існує на всій області визначення функції.
Отже, графік функції не має точок
перегину, причому
![]() на всій області визначення, тому графік
функції всюди вгнутий.
на всій області визначення, тому графік
функції всюди вгнутий.
Знайдемо
асимптоти:
![]() —
вертикальна
асимптота;
—
вертикальна
асимптота;
![]() ,
отже, похилих
асимптот
немає.
,
отже, похилих
асимптот
немає.
Графік функції не перетинається з осями координат. Початок координат є граничною точкою лівої вітки графіка.
Знайдемо
декілька допоміжних точок:
![]() .
.
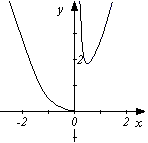
За результатами досліджень будуємо графік функції:
ВАРІАНТИ ЗАВДАНЬ КОНТРОЛЬНОЇ РОБОТИ 1
Завдання
1.1. Знайти
матрицю
![]() ,
,
