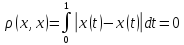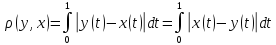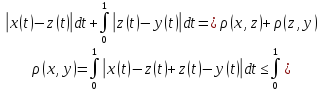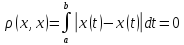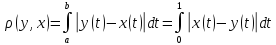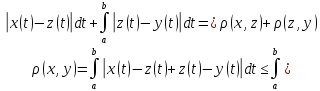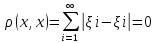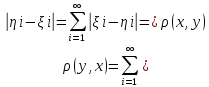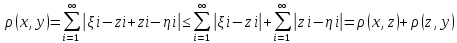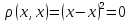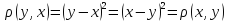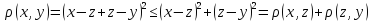lab / Лабораторна робота 2(1)

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ АВІАЦІЙНИЙ УНІВЕРСИТЕТ

ІНСТИТУТ КОМП’ЮТЕРНИХ ІНФОРМАЦІЙНИХ ТЕХНОЛОГІЙ

КАФЕДРА ПРИКЛАДНОЇ ІНФОРМАТИКИ

ЗВІТ З ЛАБОРАТОРНОЇ РОБОТИ №2

З ДИСЦИПЛІНИ: «ФУНКЦІОНАЛЬНИЙ І ОПУКЛИЙ АНАЛІЗ»

НА ТЕМУ: «МЕТРИЧНІ ПРОСТОРИ»

Виконав:

Студент ІКІТ

Гр. ТП-513

Зав'ялов Б.В

Перевірив:

Буйвол В.М

Київ – 2014

Мета роботи

Ознайомити з основними поняттями метричних просторів. Для закріплення матеріалу необхідно розв’язати приклади в яких необхідно довести чи належить та або інша множина до метричного простору.

Хід роботи

Метричний простір. Множину Х називають метричним простором, якщо кожній парі його елементів х та у поставлено у відповідність невід’ємне дійсне число 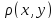таке, що для довільних трьох елементів множини Х задовільняє таким умовам:

1. , якщо х = у;

2. ;

3. ;

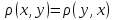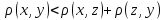Число 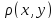при цьому називають відстанню між елементами х та у множини Х.

Метричний простір називають повним, якщо кожна фундаментальна послідовність має границю, що належить цьому ж простору

Фундаментальна послідовність. Фундаментальною послідовністю називають послідовність, члени якої як завгодно близько наближаються один до одного зі збільшенням порядкових номерів. Фундаментальні послідовності дійсних чисел завжди є збіжними.

Множина М називається щільною в G, якщо G е М. А множина М називається всюдищільною в просторі Х, якщо М = Х.

Завдання

Дослідити задану множину на визначення існування її метрики означає перевірити, чи задовільняє запропонована з метрик цим трьом аксіомам.

1. Нехай X — арифметичний п - вимірний простір, який складається з впорядкованих кортежів (су­купностей) з п дійсних чисел x=(ξ1, ξ2…ξn) y=(η1, η2…ηn). Якщо в цьому просторі ввести метрику такою формулою 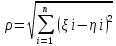то чи буде цей простір метричним?

1. ;

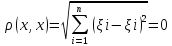2. ;

3. .

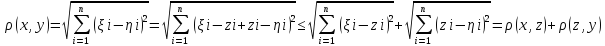Тобто множина є метрикою

2. Довести, що множина всіх многочленів степеню п, заданих на проміжку [0,1] , є мет­ричний простір.

x=(ξ1, ξ2…ξn) y=(η1, η2…ηn)

1. 

2. 

3. 

Множина є метричною

3.Довести, що множина всіх визначених і неперервних на проміжку [а, b] функцій є метричним простором. Метрику простору визначити формулою

1. 

2. 

3. 

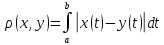
4. Довести, що простір, який складається з всіх нескінченних числових послідовностей x=(ξ1, ξ2…ξi…) , що задовольняють умову 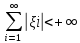, є метричним. Метрику простору

визначити формулою

1. 

2. 

3. 

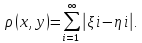
Простір є метричним

5.На множині R задана функція 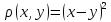. Чи є вона метрикою?

1. 

2. 

3. 

Функція є метричною

6.Чи буде метрикою формула 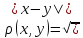, якщо x,y є R.

1.

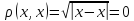
2.

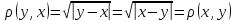
3.

Функція не є метричною

7.Відомо, що 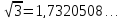Скласти збіжну послідовність наближених значень цього числа. Що можна сказати про простір, який складається з елементів xn ?

xn=(1; 1.7; 1.73; 1.732; 1.7320; 1.73205; 1.732050; 1.7320508;…). Якщо існує таке ε>0, і номер n0, починаючи з якого n>=n0, 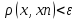, то

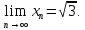
Висновок

В даній лабораторній роботі було ознайомлено з основними поняттями про метричні простори, було доведено ряд множин які або є метричним простором або ні, тобто якщо виконуються всі три аксіоми то множину можна вважати метрикою, якщо хоча б одна з аксіом не виконується то множина не може бути метричним простором.