Задание № 1. Построение гиперболы
1. На втором листе рабочей книги (назовите его Гипербола) аналогично рассмотренному примеру 1.1 самостоятельно постройте график гиперболы, описываемой уравнением
,
где аргумент х изменяется в диапазоне х[0,1; 5,1] с шагом = 0,25.
2. Сохраните рабочую книгу в папке Отчет ЛЗ-10 под именем Плоские_графики.xls.
Пример 1.2. Постройте трехмерный график гиперболоида, заданного уравнением
,
в диапазонах х[-3; 3], y[-2; 2] с шагом = 0,5 для обеих переменных.
Технология работы
Чтобы строить трехмерный график, необходимо разрешить уравнение относительно переменной z:
.
Откройте новую рабочую книгу и назовите первый лист Гиперболоид.
В А2 введите первое значение аргумента (это будет левая граница диапазона -3). В ячейку А3 введите второе значение аргумента (это будет левая граница диапазона плюс шаг построения -2,5).
Выделите блок ячеек А2:А3 и автозаполнением получите все значения аргумента (за правый нижний угол блока протяните указатель мыши до ячейки А14).
В В1 введите первое значение переменной y (это будет левая граница диапазона -2). В ячейку С1 введите второе значение y (это будет левая граница диапазона плюс шаг построения -1,5).
Выделите блок ячеек В1:С1 и автозаполнением получите все значения переменной y (за правый нижний угол блока протяните указатель мыши до ячейки J1).
В ячейку В2 введите формулу расчета переменной z:
щелчком мыши активизируйте ячейку В2 и нажмите кнопку Вставка функции
;в окне Мастер функций – шаг 1 из 2 в раскрывающемся списке поля Категория выберите Математические, а в списке Выберите функцию – КОРЕНЬ; нажмите кнопку ОК;
в поле Число окна Аргументы функции введите подкоренное выражение 1+$A2^2/9+B$1^2/4 и нажмите кнопку ОК;
автозаполнением скопируйте эту формулу в диапазон В2:J14. В результате будет получена таблица, приведенная в верхней части рис. 1.3.
Щелкните на кнопке Мастер диаграмм
и постройте график параболы:
в окне Мастер диаграмм (шаг 1 из 4) выберите Тип Поверхность, Вид – Проволочная (прозрачная) поверхность;
в окне Мастер диаграмм (шаг 2 из 4) на вкладке Диапазон данных в поле Диапазон мышью укажите диапазон данных В2:J14. В результате в поле Диапазон появится значение =Гипербола!$B$2:$J$14. Переключатель Ряды в установите в положение столбцах;
перейдите на вкладку Ряд окна Мастер диаграмм (шаг 2 из 4) и щелкните мышью в поле Подписи оси Х, наведите указатель мыши на ячейку А2, нажмите левую кнопку мыши и, не отпуская ее, протяните указатель мыши до ячейки А14, а затем отпустите левую кнопку мыши. В поле Подписи оси Х появится запись =Гипербола!$A$2:$A$14;
введите подписи оси y, для чего в поле Ряд выберите первую запись Ряд1 и в поле Имя введите первое значение -2. Затем в поле Ряд выберите вторую запись Ряд2 и в поле Имя введите второе значение -1,5. Повторите аналогично эти действия до последней записи Ряд9. После появления требуемых записей нажмите кнопку Далее;
в окне Мастер диаграмм (шаг 3 из 4) на вкладке Заголовки в поле Название диаграммы введите Двухполосный гиперболоид, аналогично в полях Ось Х (категорий), Ось Y (рядов данных) и Ось Z (значений) введите соответствующие названия x, y, z;
в окне Мастер диаграмм (шаг 4 из 4) нажмите кнопку Готово. На рабочем листе появится диаграмма, показанная на рис. 1.3 внизу.
Отформатируйте заголовки и размеры графика.
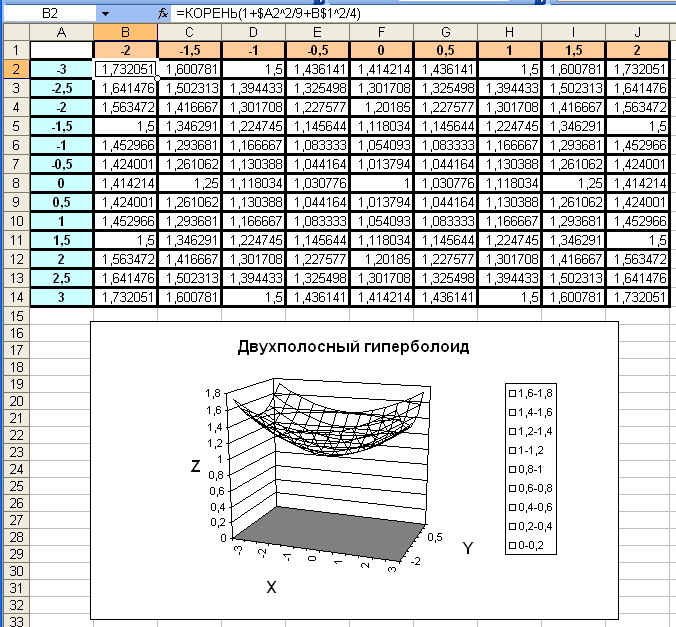
Рис. 1.3. Исходные данные и трехмерный график гиперболоида