
- •Практичне заняття № 4 Тема: Розв’язування алгебраїчних конгруенцій
- •1. Розв’язування квадратних конгруенцій за простим модулем
- •Алгоритм Шенкса -Тонеллі
- •Обчислити , ,
- •2. Алгебраїчні конгруенції -го степеня за простим модулем
- •3. Алгебраїчні конгруенції -го степеня за складеним модулем
- •4. Алгоритм Берлекемпа розкладання многочлена на незвідні множники над скінченним полем
- •Зміст практичного заняття
Зміст практичного заняття
Завдання 1. Розв’язати квадратну конгруенцію за простим модулем за алгоритмом Шенкса-Тонеллі
1)
 ; 6)
; 6)
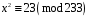 ;
;
2)
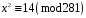 ; 7)
; 7)
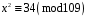 ;
;
3)
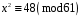 ; 8)
; 8)
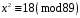 ;
;
4)
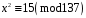 ; 9)
; 9)
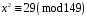 ;
;
5)
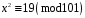 ; 10)
; 10)
 ;
;
Завдання 2. Розв’язати конгруенцію, перед цим спростивши її (знизити степінь, зменшити коефіцієнти за абсолютною величиною, зробити так, щоб старший коефіцієнт дорівнював 1):
1)
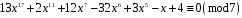 ;
;
2)
 ;
;
3)
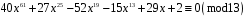 ;
;
4)
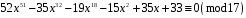 ;
;
5)
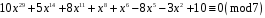 ;
;
6)
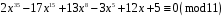
7)
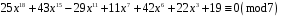 ;
;
8)
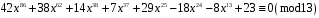 ;
;
9)
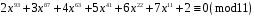 ;
;
10)
 .
.
Завдання 3. Розв’язати конгруенцію:
1)
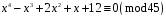 ;
;
2)
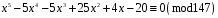 ;
;
3)
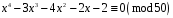 ;
;
4)
 ;
;
5)
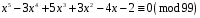 ;
;
6)
 ;
;
7)
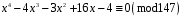 ;
;
8)
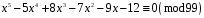 ;
;
9)
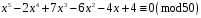 ;
;
10)
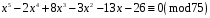 .
.
Завдання
4.
Розкласти
многочлен
 на
незвідні множники над
на
незвідні множники над
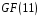 за алгоритмом Берлекемпа.
за алгоритмом Берлекемпа.
1)
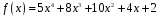 ;
;
2)
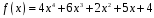 ;
;
3)
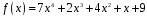 ;
;
4)
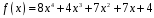 ;
;
5)
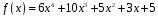 ;
;
6)
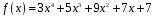 ;
;
7)
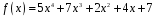 ;
;
8)
 ;
;
9)
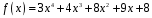 ;
;
10)
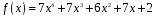 .
.
Контрольні питання
-
Що таке квадратна конгруенція за простим модулем?
-
За якої умови квадратна конгруенція за простим модулем має розв’язки?
-
Як розв’язується квадратна конгруенція у випадках
 ,
,
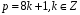 ?
? -
У чому полягає алгоритм Шенкса-Тонеллі?
-
Як спростити алгебраїчну конгруенцію
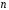 -го
степеня за простим модулем?
-го
степеня за простим модулем? -
Скільки розв’язків має алгебраїчна конгруенція
 -го
степеня за простим модулем?
-го
степеня за простим модулем? -
Як знайти розв’язки алгебраїчної конгруенції
 -го
степеня за простим модулем?
-го
степеня за простим модулем? -
Як розв’язується алгебраїчна конгруенція
 -го
степеня за складеним модулем у випадку,
коли канонічний розклад модуля має
лише прості множники?
-го
степеня за складеним модулем у випадку,
коли канонічний розклад модуля має
лише прості множники? -
Як розв’язується алгебраїчна конгруенція
 -го
степеня за складеним модулем у випадку,
коли канонічний розклад модуля містить
степінь простого числа?
-го
степеня за складеним модулем у випадку,
коли канонічний розклад модуля містить
степінь простого числа? -
У чому полягає алгоритм Берлекемпа розкладання многочлена на незвідні множники над скінченним полем?
Література:
-
Василенко О.С. Теоретико-числовые алгоритмы в криптографии. – М.: МНЦНО, 2003. – 328 с.
-
Виноградов И.М. Основы теории чисел. – М.: Наука, 1981. – 176 с.
-
Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т.– М.: Мир, 1988. – Т.1. – 430 с., Т.2. – 392 с.
-
Матемтические и компьютерные основы криптологии: Уч. пос. / Ю.С. Харин, В.И. Берник, Г.В. Матвеев, С.В. Агиевич. – МН.: Новое знание, 2003. – 382 с.
Порядок виконання роботи.
-
Вивчити короткі теоретичні відомості з теми заняття, користуючись конспектом лекції і рекомендованою літературою.
-
Виконати практичні завдання за своїм варіантом.
-
Скласти звіт, приєднавши отримані результати.
Вимоги до звіту.
У звіті мають бути приведені:
-
Короткі відомості з теми заняття.
-
Розв’язання свого варіанту з необхідними поясненнями.
-
Відповіді на контрольні питання.
