4. Числові характеристики розподілу випадкових величин

Основною характеристикою випадкової величини є її закон розподілу. Але далеко не в кожній задачі потрібно знати весь закон розподілу. У ряді випадків випадкову величину можна охарактеризувати одним чи декількома числами, що називаються числовими характеристиками випадкової величини (чи відповідного закону розподілу).

1) Характеристики положення а) Математичне сподівання випадкової величини

Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання. Термін «математичне сподівання» випадкової величини є синонімом терміна «середнє значення» випадкової величини.

Означення. Математичним сподіванням дискретної випадкової величини , яка набуває значень із скінченної множини чисел , називається число

, (5)

яке дорівнює сумі добутків значень випадкової величини на відповідні ймовірності.

Означення. Математичним сподіванням неперервної випадкової величини , яка має щільність розподілу , називається число

(6)

Властивості математичного сподівання

1. Математичне сподівання сталої величини С дорівнює самій сталій:

.

Справді, сталу можна розглядати як випадкову величину, що з ймовірністю, яка дорівнює одиниці, набуває значення, а тому.

2. Сталий множник можна виносити за знак математичного сподівання:

3. Математичне сподівання суми двох випадкових величин дорівнює сумі математичних сподівань цих величин, тобто

Ця властивість виконується і для будь-якого скінченого числа випадкових величин.

4. Якщо дві випадкові величини незалежні, то математичне сподівання їх добутку дорівнює добутку математичних сподівань цих величин, тобто

Ця властивість виконується і для будь-якого скінченого числа незалежних випадкових величин.

Якщо випадкова величина , то, а саме: математичне сподівання випадкової величини маєобов’язково міститися всередині інтервалу , являючи собою центр розподілу цієї величини.

Приклад 5. Закон розподілу дискретної випадкової величини задано таблицею (приклад 1):

	–4	–1	2	6	9	13
	0,1	0,2	0,1	0,3	0,1	0,2

Обчислити .

Розв’язання: За формулою (1)

.

Приклад 6. За заданою щільністю ймовірностей (приклад 2)

знайти .

Розв’язання. За формулою (2)

.

Б) Мода та медіана випадкової величини

Означення. Модою () дискретної випадкової величининазивається те її можливе значення, якому відповідає найбільша ймовірність.

Якщо випадкова величина має одну моду, то такий розподіл ймовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і т. ін. Існують і такі розподіли, які не мають моди. Їх називають антимодальними.

Приклад 7. Для дискретної випадкової величини з прикладу 1 .

Означення. Модою неперервної випадкової величини Х називаються те її можливе значення, якому відповідає максимальне значення щільності ймовірності:

. (7)

Означення. Медіаною () випадкової величининазивається те її значення, для якого функція розподілу задовольняє умові

(8)

Приклад 8. Для неперервної випадкової величини з прикладу 2 питання 5, заданої щільністю ймовірностей

знайти , .

Розв’язання. Графік щільності зображено на малюнку:

Згідно з графіком маємо . Отже,.

Визначимо . Для цього знайдемо функцію розподілу:

Отже,

Для визначення застосовуємо рівняння (3):

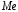можна також знайти, скориставшись щільністю ймовірностей:

,

або при :

.

Отже, — таке можливе значення випадкової величини , що пряма, проведена перпендикулярно до відповідної точки осінаплощині, поділяє площу фігури, яка обмежена функцією на дві рівні частини.