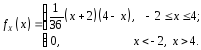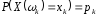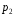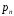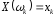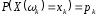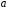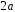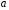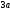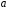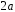Ю.Д.Жданова. Лекції з ВГПМ. М3 Вибрані глави ТЙіМС. Лекція № 9

Лекція № 9 Тема: Випадкові величини і розподіли

План лекції:

1. Випадкові величини.

2. Функція розподілу випадкової величини.

3. Щільність розподілу.

4. Числові характеристики розподілу випадкових величин.

1. Випадкові величини

Нехай заданий деякий ймовірнісний простір 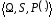, де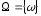– простір елементарних подій деякого випадкового експерименту,–-алгебра подій,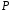– ймовірність, тобто числова функція, визначена на, яка задовольняє аксіомам Колмогорова.

Означення. Випадковою величиною називається числова функція від елементарної події, якщо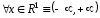подія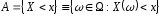належить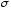-алгебрі, тобто визначена ймовірність.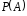

Функція 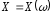відображає множину 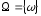на одновимірний простір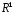: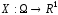. У цьому випадку випадкову величину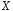називаютьодновимірною.

Випадкові величини позначають великими буквами латинського алфавіту 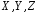,…, а їх можливі значення — малими .

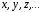Кожній випадковій величині ставиться у відповідність деяка числова множина – множина значень випадкової величини.

Випадкові величини за виглядом множини значень можна розділити на дві категорії.

Означення. Дискретною випадковою величиною називається така величина, яка в результаті експерименту може набувати скінченну або зчисленну множину значень.

Означення. Неперервною випадковою величиною називається така величина, яка в результаті експерименту може набувати будь-яких невід’ємних значень з деякої неперервної множини від 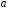до b (можливо, від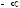до).

Але знання однієї лише множини можливих значень недостатньо для повного опису випадкової величини. Необхідно ще знати, з якою ймовірністю випадкова величина попадає в ту чи іншу підмножину множини дійсних чисел. Цього можна дізнатися із закону розподілу випадкової величини.

Означення. Законом розподілу випадкової величини називається будь-яке правило, що встановлює зв'язок між можливими значеннями випадкової величини і їхніми ймовірностями.

Закон розподілу є повною характеристикою випадкової величини. Він може мати різні форми: функція розподілу, щільність розподілу, таблиця ймовірностей окремих значень випадкової величини та ін.

Закон розподілу дискретної випадкової величини 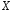задається таблицею

			...		...
			...		...

(1)

Числа називаютьсяможливими значеннями випадкової величини 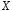, а числаназиваютьсяймовірностями цих значень. Набір чисел 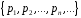називаєтьсярозподілом ймовірностей випадкової величини . Необхідною є така умова

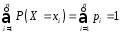(2)

Рівність (2) називають умовою нормування для дискретної випадкової величини .

Приклад 1. Закон розподілу дискретної випадкової величини задано таблицею

	–4	–1	2	6	9	13

1) Знайти ймовірності можливих значень випадкової величини .

2) Обчислити ймовірності таких випадкових подій: 1) 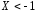; 2); 3); 4).

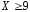Розв’язання. За умовою нормування (2) дістанемо:

;

;

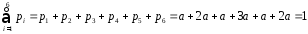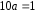Отже, для того, щоб таблицею, заданою в умові, визначався закон розподілу дискретної випадкової величини, необхідно щоб :

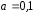	–4	–1	2	6	9	13
	0,1	0,2	0,1	0,3	0,1	0,2

2) Обчислимо ймовірності подій:

1) ;

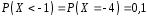2) ;

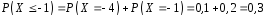3)

;

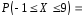
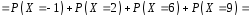
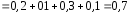4) .

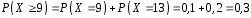Для неперервної випадкової величини 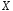закон розподілу задається за допомогою кусково–неперервної функції – щільності ймовірності, так, що для будь-яких 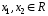справедлива рівність:

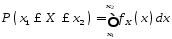, (3)

причому 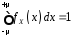. (4)

Рівність (4) називають умовою нормування для неперервної випадкової величини .

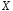Приклад 2. За заданою щільністю ймовірностей

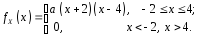
знайти параметр .

Розв’язання. За умовою нормування маємо:

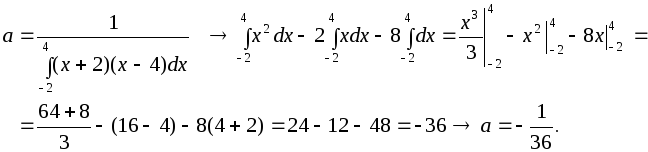
Щільність ймовірностей із знайденим 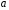матиме вигляд