6. Зразки виконання і оформлення контрольних практичних завдань Розділ 1 Прикладні аспекти лінійної алгебри

Тема 1. Скінченновимірні векторні простори

Завдання 1. Обчислити коефіцієнти лінійної залежності системи ненульових векторів над полем :

; ;

; ;

; .

Розв’язання. Якщо система векторів лінійно залежна, то довільний векторз неї можна представити як лінійну комбінацію інших векторів системи, що дає систему рівнянь . Таким чином, достатньо знайти числа з поля , тобто знайти розв’язок системи виду , де стовпці матриціутворені координатами векторів системи.

Виберемо, наприклад, вектор , тоді будемо мати систему рівнянь

,

або

.

або

.

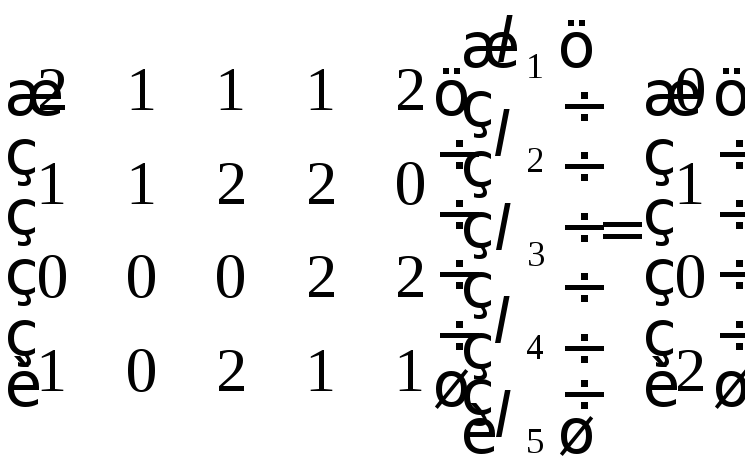Розв’яжемо цю систему методом Гаусса. Визначимо ранг розширеної матриці системи :

.

Очевидно , отже, система сумісна. А оскільки, то система невизначена, тобто має безліч розв’язків.

Невідомі ,і– базисні, невідоміі– вільні.

Продовжимо перетворення матриці так, щоб базисні невідомі виявилися на головній діагоналі одиничної матриці:

Після всіх перетворень отримали матрицю, яка відповідає системі:

звідки

або

Надаючи довільні значення вільним змінним і, ми легко безпосередньо знайдемо,і. Нехай, наприклад,,, тодіє одним з шуканих розв’язків системи.

Дійсно,

.

Інші розв’язки виходять за рахунок довільних значень і.

Завдання 2. Обчислити розмірність векторного простору над полем , який є лінійною оболонкою (сукупністю лінійних комбінацій) системи векторів.

Розв’язання. Розмірність векторного простору над полем –це число векторів базису простору – максимальне число лінійно незалежних векторів цього простору. Визначимо це число.

Якщо система векторів лінійно незалежна, то лінійна комбінація векторів системи при , які не всі водночас дорівнюють нулю. Таким чином, достатньо знайти числа з поля , тобто знайти розв’язок системи виду , де стовпці матриціутворені координатами векторів системи:

Розв’яжемо цю однорідну систему методом Гаусса.

.

Отримали, що рівність

можлива лише при . А це означає, що вектори лінійно незалежні, тобто утворюють базис. Таким чином, розмірність векторного простору над полем дорівнює 3.

Тема 2. Лінійні оператори в векторних просторах

Завдання 3. Побудувати характеристичний та мінімальний многочлени матриці над полем .

Розв'язання. Побудуємо характеристичний многочлен матриці :

Характеристичний многочлен матриці має єдиний корінь кратності . При цьому

,

,

,

.

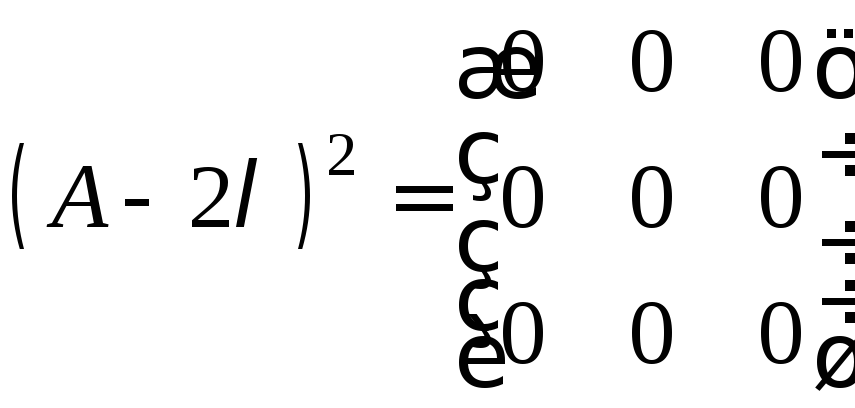Отже, і мінімальний многочлен є .

Другий спосіб побудови мінімального многочлена.

За теоремою про анулюючий многочлен мінімальним многочленом може бути один з многочленів , , . Треба перевірити, які з цих многочленів є анулюючими і вибрати з них многочлен мінімального степеня.

;

Анулюючими є і . Мінімальний степінь має . Отже, мінімальний многочлен є .

Завдання 4. Побудувати мінімальний многочлен вектора відносно матрицінад полем .

,

Розв'язання. Побудуємо послідовність , яка є періодичною:

;

;

;

;

;

;

;

;

.

Отже, вектори будуть лінійно незалежні, а векторбуде лінійною комбінацією цих векторів з коефіцієнтами з поля . Визначимо коефіцієнти лінійної комбінації

для чого розв’яжемо систему рівнянь:

Невідомі ,базисні, невідомі,,,,,– вільні.

або

Надаючи довільні значення вільним змінним ,,,,,, знайдемо,. Нехай, наприклад,,,,,,, тодіє одним з шуканих розв’язків системи .

Значить, мінімальним многочленом вектора відносно матрицібуде многочлен

.