
1. Монотонність та екстремуми функції
 Означення.
Функцію
Означення.
Функцію
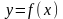 називають зростаючою (спадною) в проміжку
(а, в), якщо більшому значенню аргументу
в цьому проміжку відповідає більше
(менше) значення функції, тобто якщо із
нерівності х2
х1 випливає нерівність
називають зростаючою (спадною) в проміжку
(а, в), якщо більшому значенню аргументу
в цьому проміжку відповідає більше
(менше) значення функції, тобто якщо із
нерівності х2
х1 випливає нерівність
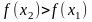 ,
то функція
,
то функція
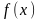 -
зростаюча, а якщо
-
зростаюча, а якщо
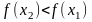 ,
то функція - спадна.
,
то функція - спадна.
Функцію називають монотонною в проміжку (а, в), якщо вона в цьому проміжку зростаюча або спадна. Проміжки, в яких функція монотонна називають проміжками монотонності цієї функції.
Достатня ознака монотонності функції
Якщо похідна диференційовної функції додатна всередині деякого проміжку, то функція зростає в цьому проміжку. Якщо похідна диференційованої функції від’ємна всередині деякого проміжку, то функція спадає в цьому проміжку.
Для знаходження інтервалів монотонності заданої функції доцільно дотримуватись такого порядку дій:
1. знайти область визначення та
похідну
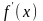 ;
;
2. знайти корені рівняння
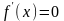 ;
;
3. поділити область визначення функції знайденими коренями рівняння на інтервали знакової постійності ;
4. визначити знак похідної в кожному інтервалі і зробити висновок, в якому інтервалі функція зростає, а в якому спадає.
З найти
інтервали зростання і спадання функції
найти
інтервали зростання і спадання функції
 .
.
● Маємо
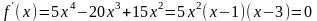 ,
,
звідки

Похідна f
(x)
неперервна для х(–
;
+ )
і перетворюється на нуль лише в точках
х
= 0, х
= 1, х
=3, тому вона в інтервалах (– ;
0), (0; 1), (1; 3) і (3; + )
зберігає знак. Оскільки f(–
1) > 0,
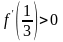 ,
f
(2) < 0,
f
(5) > 0,
f
(х) > 0,
якщо х(–
;
0), f
(х) > 0,
х(0;
1), f
(х) < 0,
х(1;
3), f
(х) > 0,
х(3;
+ ).
,
f
(2) < 0,
f
(5) > 0,
f
(х) > 0,
якщо х(–
;
0), f
(х) > 0,
х(0;
1), f
(х) < 0,
х(1;
3), f
(х) > 0,
х(3;
+ ).
Тому функція f(x) зростає на інтервалах (– ; 0); (0; 1); (3; + ) і спадає на інтервалі (1; 3).
Означення.
Функція
має при х=х0 максимум
(мінімум), якщо існує такий окіл точки
х0, для усіх точок х якого
виконується нерівність:
 для максимуму,
для максимуму,
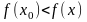 для мінімуму.
для мінімуму.
Екстремум функції - це узагальнений термін понять максимуму та мінімуму. Значення аргументу х = х0, при якому функція має екстремум (максимум або мінімум) називають точкою екстремуму функції (максимуму або мінімуму, відповідно).
Означення. Критичними точками першого роду функції називають точки, в яких не існує або дорівнює нулю.
Рівність називають необхідною умовою існування екстремуму функції . Щоб визначити, в яких з критичних точок функція має екстремум і який саме, використовують достатні умови існування екстремуму.
Достатні умови існування екстремуму функції
Якщо функція диференційовна в околі критичної точки першого роду х = х0 і її похідна :
при х х0 - додатна, а при х х0 - від’ємна, то в точці х0 функція має максимум;
2. при х х0 - від’ємна, а при х х0 - додатна, то в точці х0 функція має мінімум;
3. зліва та справа від точки х0 має однаковий знак, то в точці х0 функція не має екстремуму.
Порядок дій при дослідженні функції на екстремум:
1. знаходять похідну заданої функції;
2. знаходять критичні точки першого роду (значення х, при яких не існує або дорівнює нулю);
3. визначають знак зліва та справа в околі кожної критичної точки;
4. роблять висновок, чи має функція екстремум і який саме у знайдених критичних точках;
5. обчислюють екстремальні значення функції в точках екстремуму.
Дослідження функції на екстремум доцільно виконувати з використанням таблиці по аналогії з наведеним нижче прикладом.
З найти екстремуми функції
у = 2х3 – 9х2 + 12х + 5.
Розв’язання. Знаходимо похідну:
 = 6х2 – 18х + 12 = 6(х – 1) (х
– 2)
= 6х2 – 18х + 12 = 6(х – 1) (х
– 2)
Знаходимо критичні точки першого роду: із рівності
6(х – 1)(х – 2) = 0
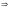 х1 = 1, х2 = 2.
х1 = 1, х2 = 2.
Інших точок не має, тому що
визначена при всіх
 .
.
Критичні точки х1 та х2
поділяють область визначення функції
 на інтервали постійного знаку похідної
(критичні точки та відповідні інтервали
записуємо у перший рядок таблиці 1).
на інтервали постійного знаку похідної
(критичні точки та відповідні інтервали
записуємо у перший рядок таблиці 1).
Визначаємо знак
 в
кожному інтервалі (записуємо ці знаки
у другий рядок таблиці 1).
в
кожному інтервалі (записуємо ці знаки
у другий рядок таблиці 1).
Згідно з достатніми умовами існування екстремуму функції робимо висновок відносно кожної критичної точки (характер поведінки функції вказуємо у третьому рядку таблиці 1).
-
x
1
(1, 2)
2


+
0
—
0
+


max
min
Обчислимо максимальне та мінімальне значення функції:
 ;
;
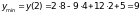 .
.
