Тема 6. Розв’язування систем лінійних алгебраїчних рівнянь над скінченними полями

Завдання 3. Розв’язати в цілих числах рівняння

.

№ варіанту
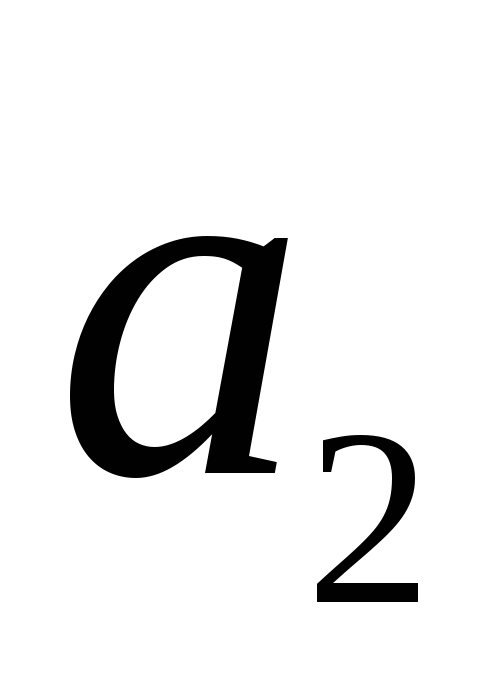
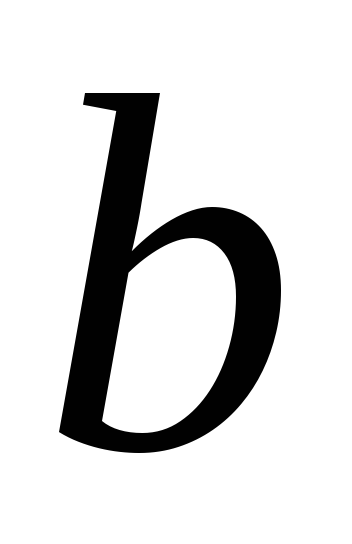
1	1	3	–2	11
2	4	–1	–1	–14
3	–2	4	1	9
4	1	–3	7	–3
5	–5	–1	2	–6
6	5	–2	3	13
7	3	–1	2	19
8	–4	2	1	–11
9	3	–2	1	–5
10	2	–4	–1	8

Завдання 4. Розв’язати в цілих числах систему лінійних алгебраїчних рівнянь

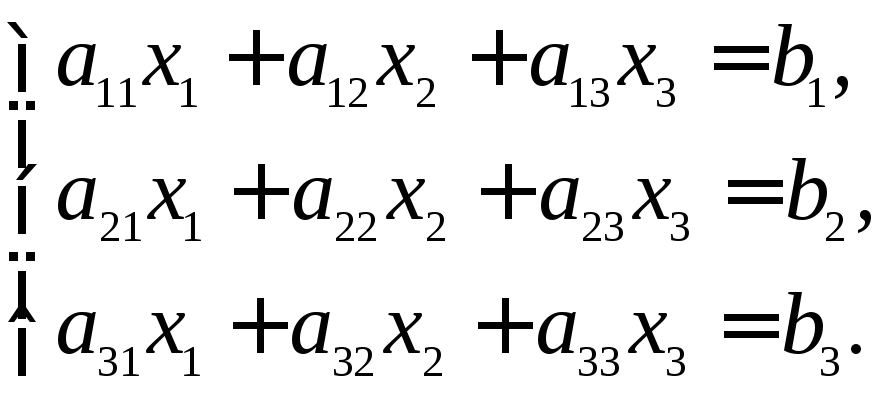
№ варіанту
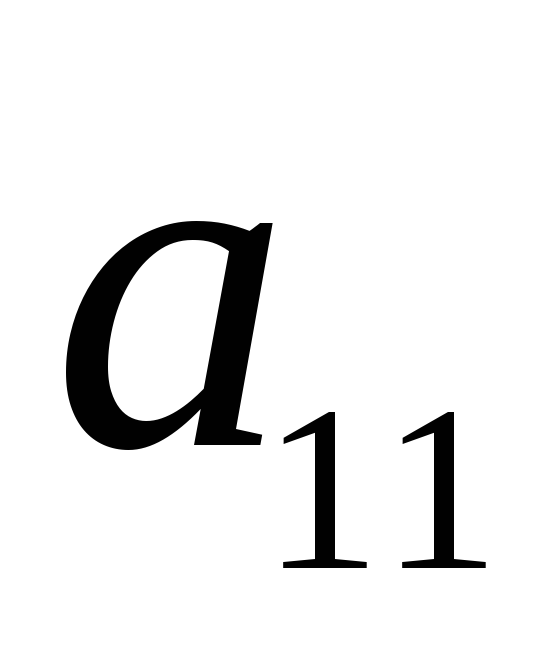
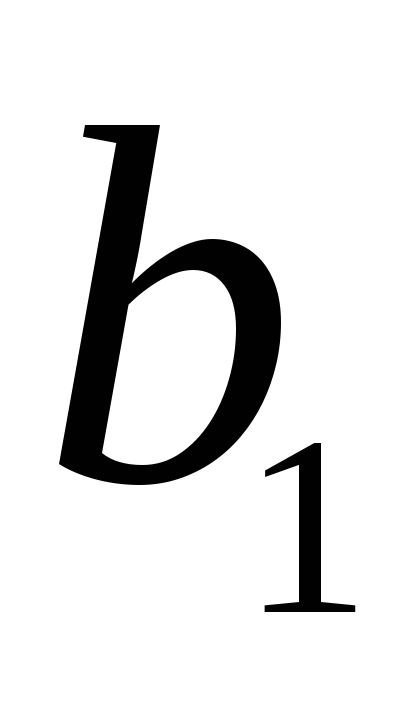
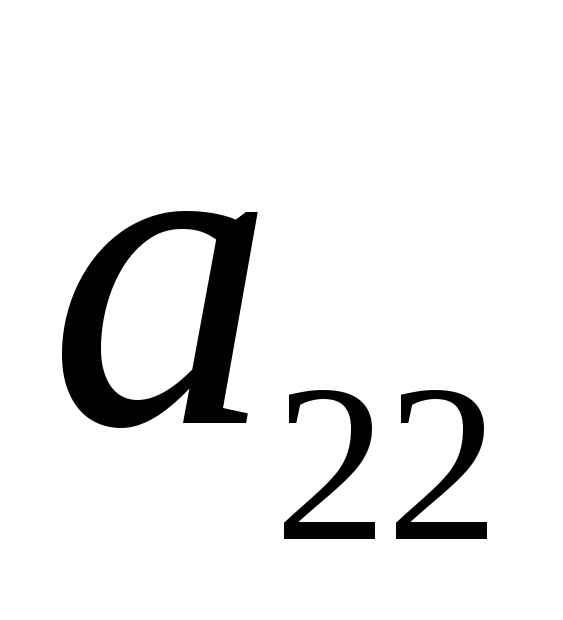
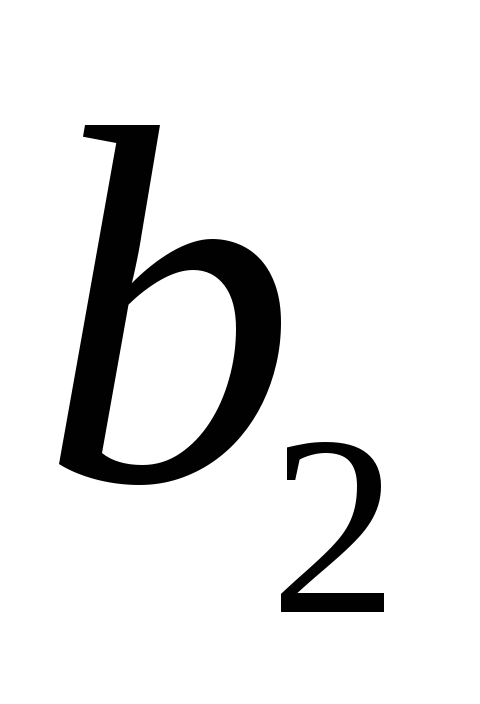
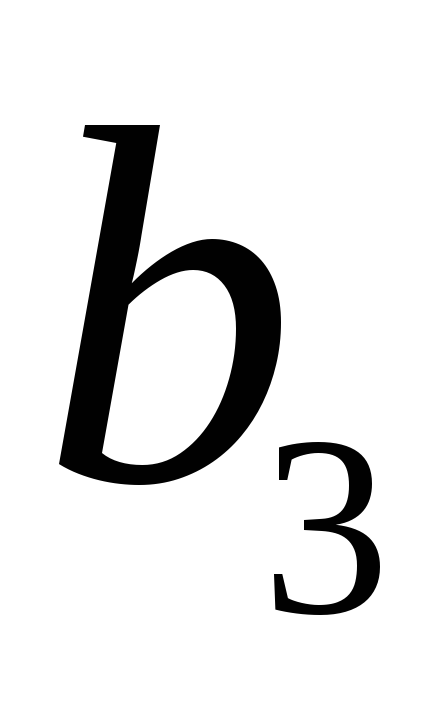
1	1	3	–2	11	–2	5	2	7	3	–2	–1	–3
2	4	–1	–1	–14	–1	–2	2	9	–3	2	–1	2
3	–2	4	1	9	2	–1	–2	7	–1	3	2	–3
4	–1	–3	7	–3	2	1	–2	2	–1	–5	2	15
5	–5	–3	2	–6	4	–1	1	5	–1	3	–1	–8
6	–5	–2	3	3	–3	–1	4	6	–1	2	–1	–5
7	3	–1	2	19	–2	–1	2	9	1	4	1	–5
8	–4	2	1	–11	–1	1	3	3	–3	–2	–1	4
9	3	–2	1	–5	–3	1	–1	1	–1	–4	–4	–6
10	2	–4	–1	8	1	2	–1	–1	3	–1	–4	2

Розділ 3 Вибрані глави теорії ймовірностей і математичної статистики

Тема 8. Розподіли ймовірностей випадкових величин

Завдання 1. Прилад складається з елементів, працюючих незалежно один від одного. Ймовірність відмови кожного елемента дорівнює. Випадкова величина– число елементів, що відмовили. Знайти

а) закон розподілу випадкової величини ;

б) функцію розподілу випадкової величини та її графік;

в) математичне сподівання , дисперсію, середнє квадратичне відхилення.

№ варіанту
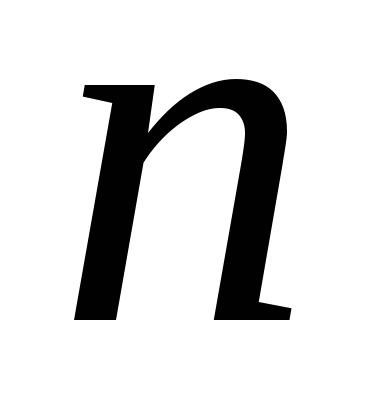
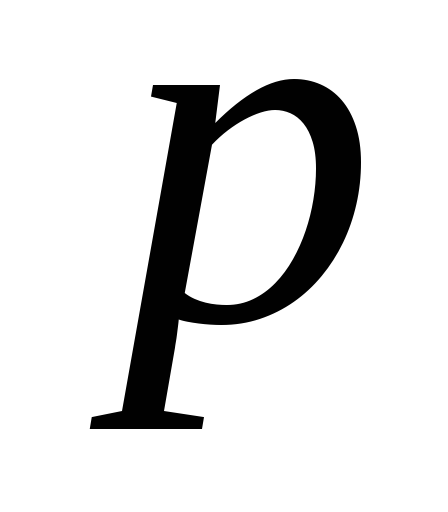
1	3	0,08
2	4	0,06
3	5	0,07
4	3	0,09
5	4	0,05
6	5	0,15
7	3	0,25
8	4	0,45
9	5	0,55
10	3	0,35

Завдання 2. Випадкова величина розподілена за рівномірним законом.

а) Написати вираз для функції розподілу і щільності, якщо відомо, що,і для будь-якого інтервалувиконується умова.

б) знайти математичне сподівання , дисперсію, середнє квадратичне відхилення.

№ варіанту
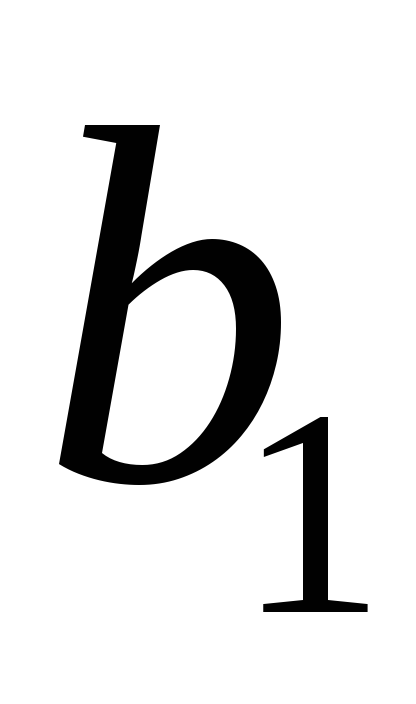
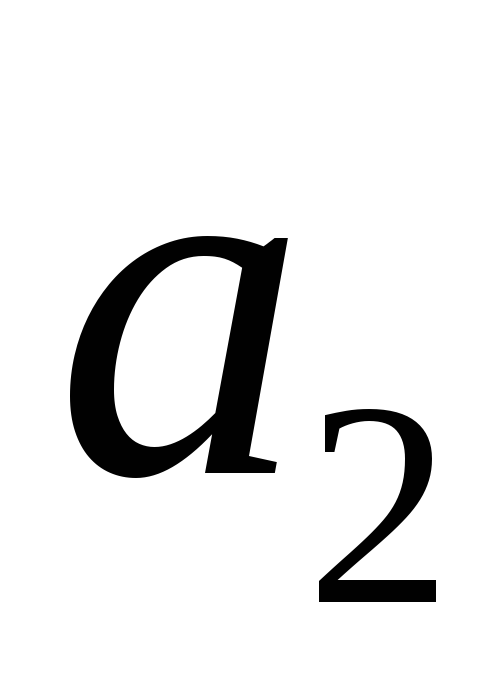
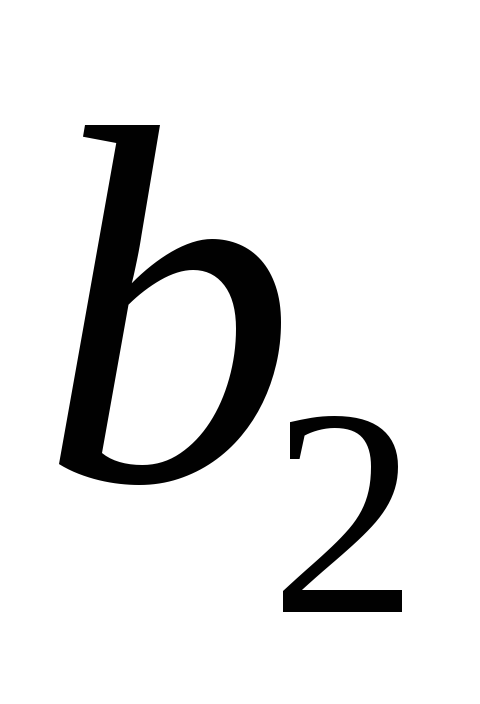
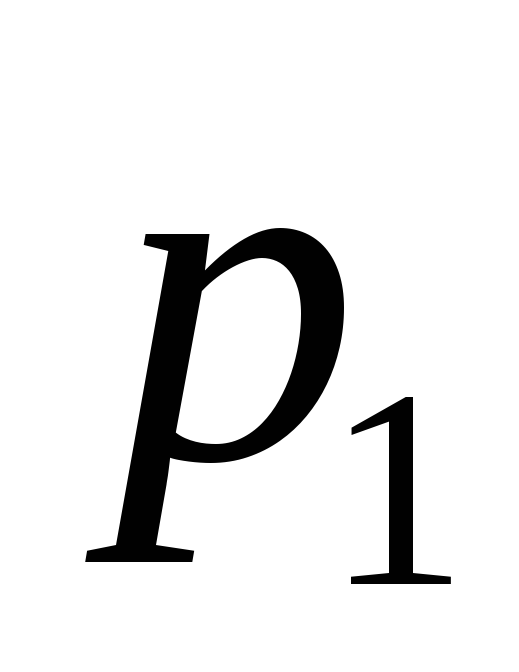
1	2	4	0	2	2/9
2	1	3	3	6	3/8
3	4	6	2	4	4/7
4	3	5	5	8	5/6
5	6	9	3	6	1/5
6	0	1,5	1,5	4	4/9
7	2,5	6	1,5	2,5	5/8
8	0	1,1	1,1	2	3/5
9	0,5	1	1	2	1/5
10	2	4	1	2	7/10

Завдання 3. Випадкова величина розподілена за нормальним законом з параметрами і .

а) Написати вираз для функції розподілу і щільності;

б) знайти .

№ варіанту
1	10	1	12	14
2	9	2	10	12
3	8	3	9	12
4	7	4	5	7
5	6	5	3	5
6	5	6	0	3
7	3	8	–1	2
8	14	10	12	15
9	9	2	8	11
10	10	4	5	18