Тема 3. Лінійні рекурентні послідовності над полем

Завдання 5. Побудувати розгортку двійкового регістру зсуву з лінійним зворотним зв’язком – рекурентну послідовність довжининад полем з примітивним мінімальним многочленом і початковим станом, що задане в шістнадцятковій системі числення. Розгортка регістру – вправо, початкове заповнення доповнити до довжини регістру нулями зліва.

Розв'язання. Для поліному рекурентне співвідношення, що задає послідовність, має вид . При початковому стані отримаємо

.

Крім того, перевірочне співвідношення має вид (решта змінних входять з нульовими коефіцієнтами). Очевидно, воно вкладається на довжині послідовності декілька разів.

Розділ 2 Теоретико-числові обчислювальні алгоритми

Тема 4. Розв’язування алгебраїчних конгруенцій

Завдання 1. Розв’язати квадратну конгруенцію за простим модулем за алгоритмом Шенкса-Тонеллі.

Розв’язання

1. Обчислимо значення символу Лежандра

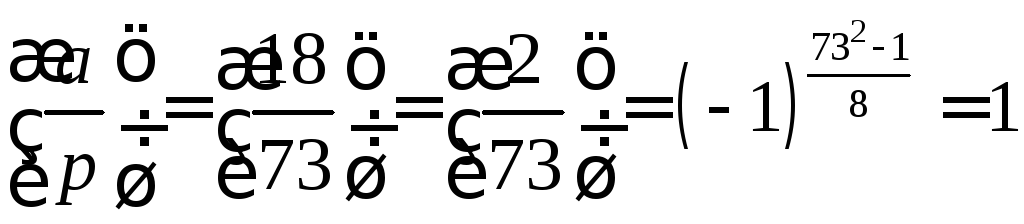
Отже, конгруенція має розв’язки.

2. Запишемо число 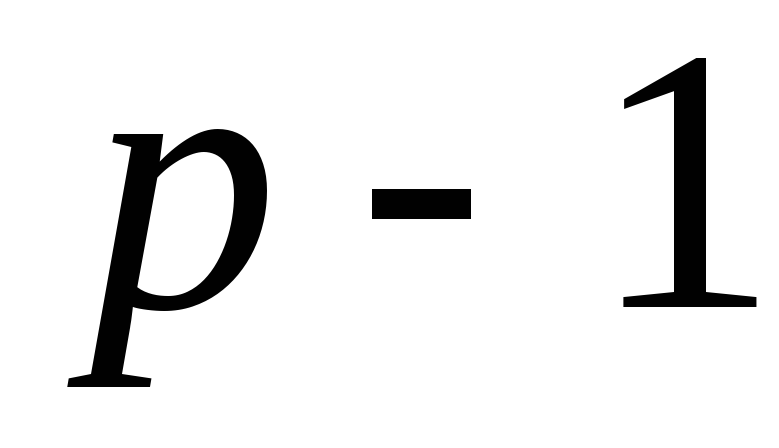у вигляді добутку парного і непарного чисел: 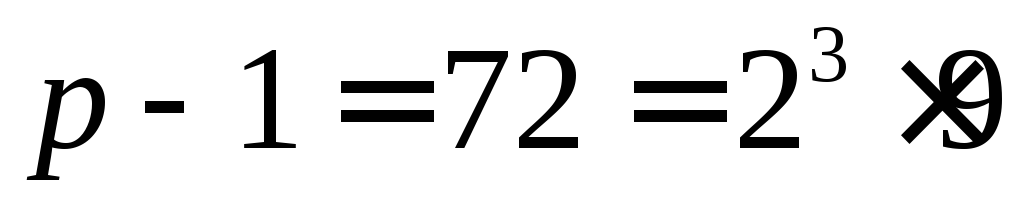. Отже, , .

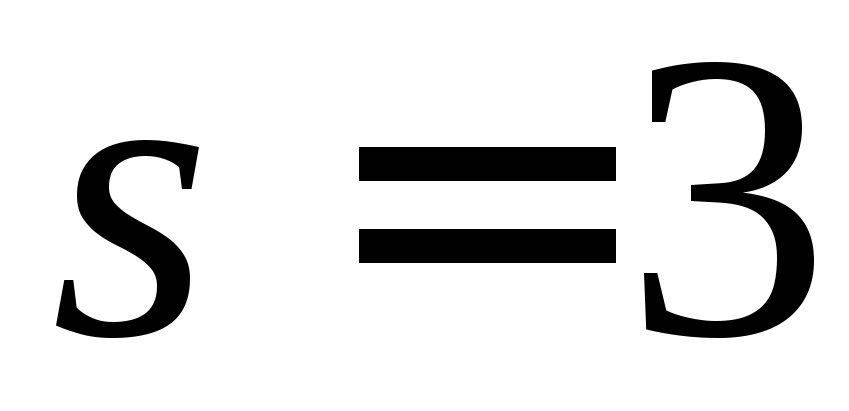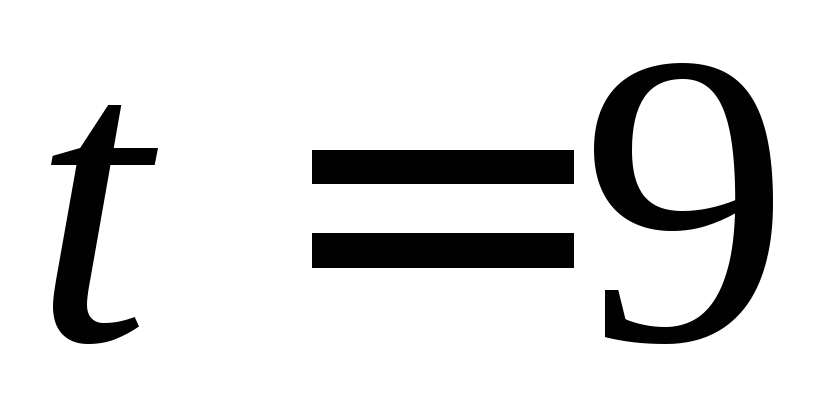3. Знайдемо квадратичний нелишок 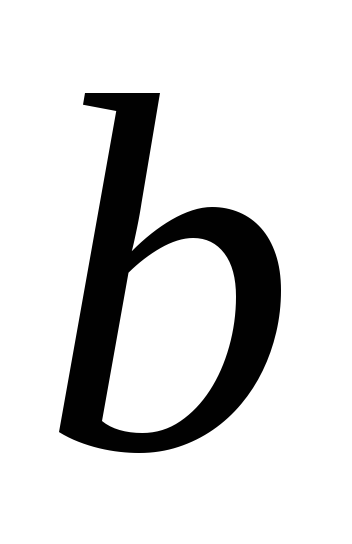за модулем 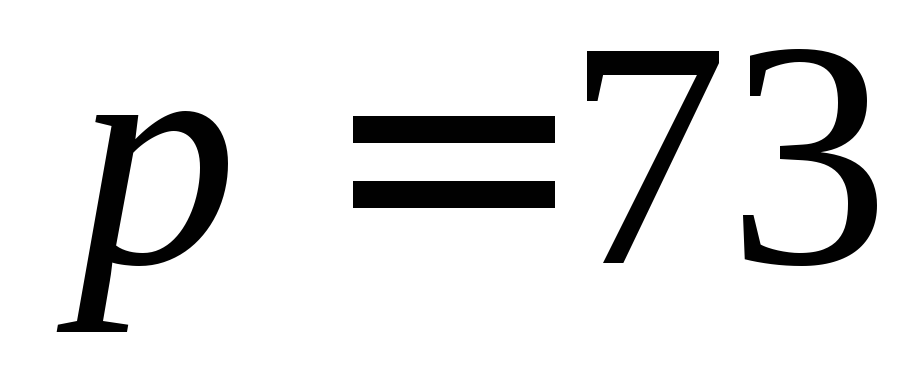. Нехай 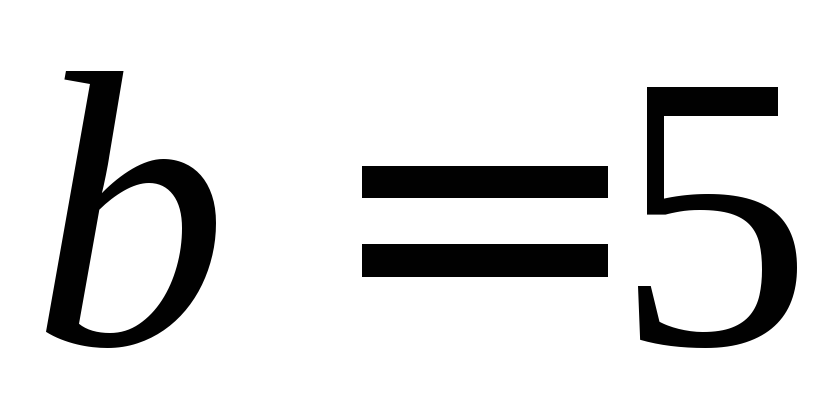, тому що

.

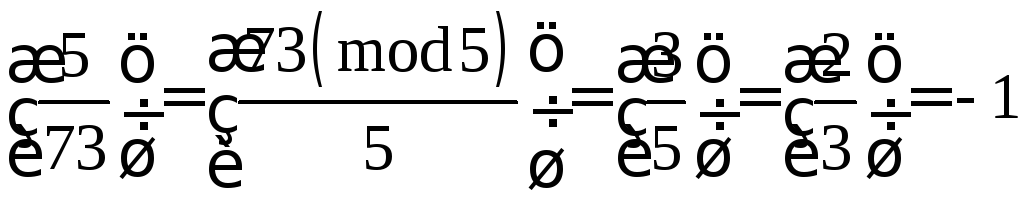4. Покладемо .

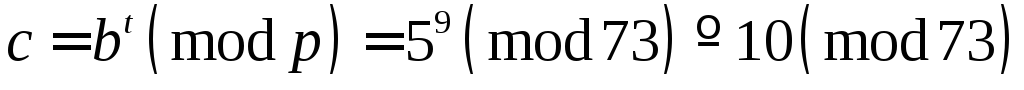5. Обчислимо ,

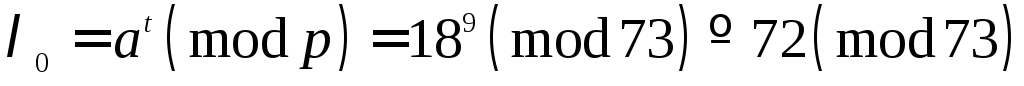6. Обчислимо порядок :

.

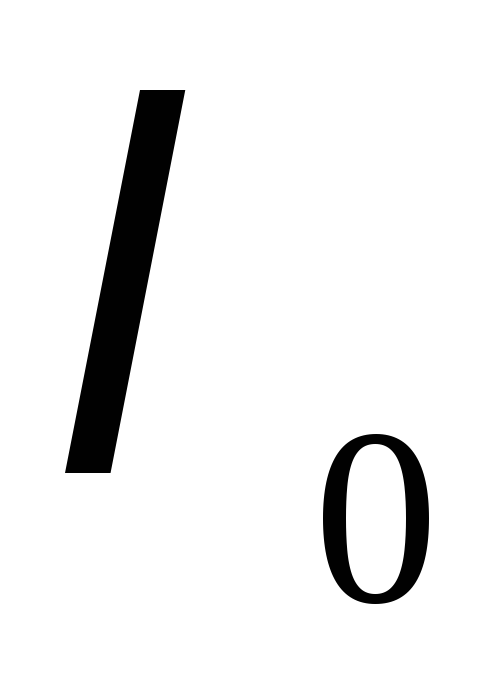Звідси, ,.

7. Обчислимо степінь 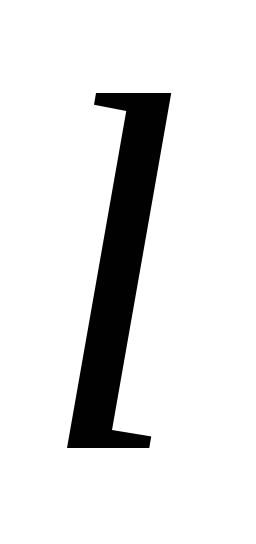, в який треба підносити:.

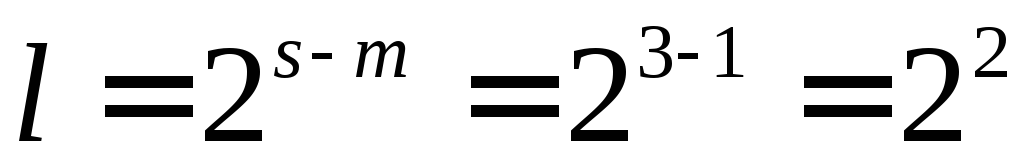8. Обчислимо

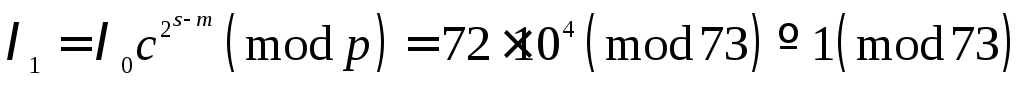
9) Перевірка: .

Завдання 2. Спростити конгруенцію (знизити степінь, зменшити коефіцієнти за абсолютною величиною, зробити так, щоб старший коефіцієнт дорівнював 1) і розв’язати:

.

Розв’язання. Знизимо степінь конгруенції.

Помічаємо, що не є розв’язком даної конгруенції, значить . Тоді за теоремою Ферма . Враховуючи це, маємо:

;

;

;

.

Отже, задана конгруенція еквівалентна конгруенції

,

яку після зведення подібних доданків запишемо у вигляді:

.

Замінимо останню конгруенцію на еквівалентну конгруенцію, старший коефіцієнт якої рівний 1. Для цього розв’яжемо конгруенцію

і знайдемо . Дана конгруенція еквівалентна конгруенції

тобто конгруенції

.

Розв’яжемо отриману конгруенцію. За теоремою про число розв’язків конгруенції -го степеня за простим модулем отримана конгруенція має не більше 5 коренів.

Запишемо повну систему абсолютно найменших лишків за модулем :

0, 1, 2, 3, –3 ,–2, –1.

Підставимо числа цієї системи в отриману конгруенцію. Будемо мати:

;

; ;

; ;

; .

Таким чином, клас є розв'язком даної конгруенції.

Тема 6. Розв’язування систем лінійних алгебраїчних рівнянь над скінченними полями

Завдання 3. Розв’язати в цілих числах рівняння

.

Розв’язання. Складемо матрицю

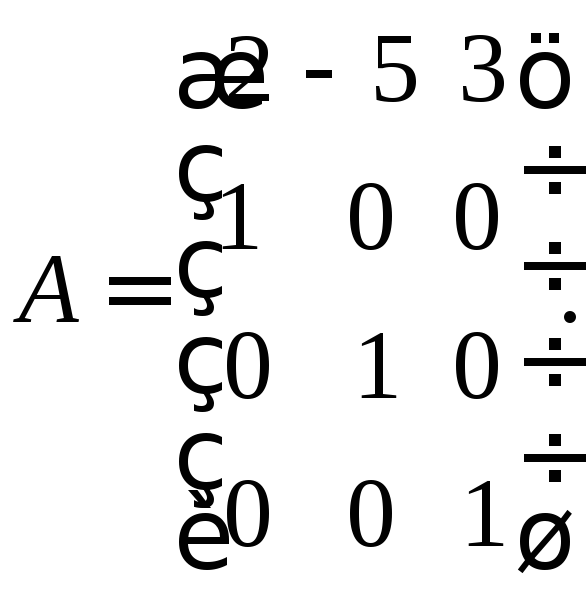
Вибираємо в першому рядку матриці найменший за абсолютною величиною ненульовий елемент . Йдучи за алгоритмом знаходження всіх цілочислових розв’язків лінійного алгебраїчного рівняння, будемо мати:

Оскільки , то загальний розв’язок заданого рівняння в цілих числах має вигляд

,

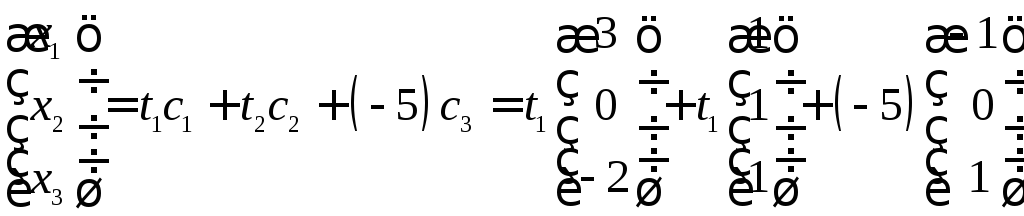де , а вектори– це стовпці матриці. Покладаючи, наприклад,, знаходимо

.

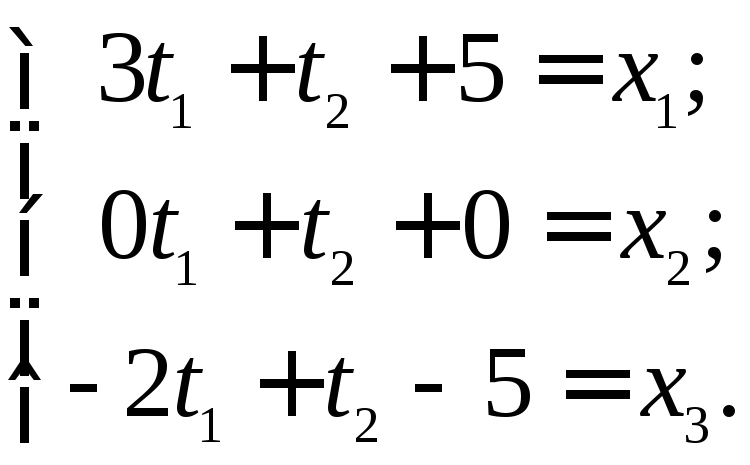
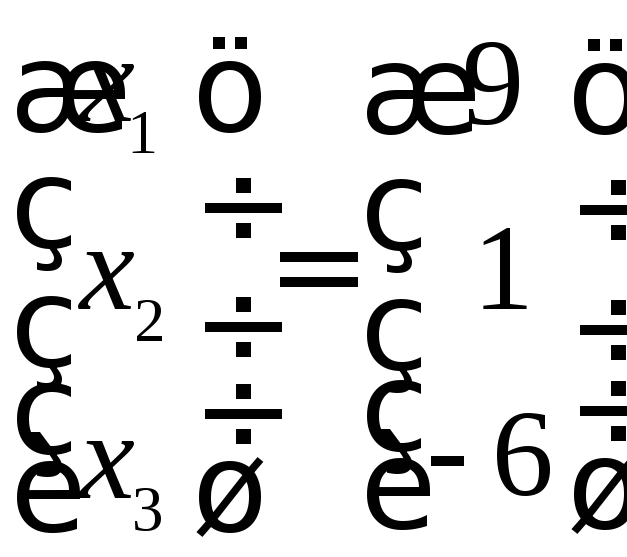Відповідь: .

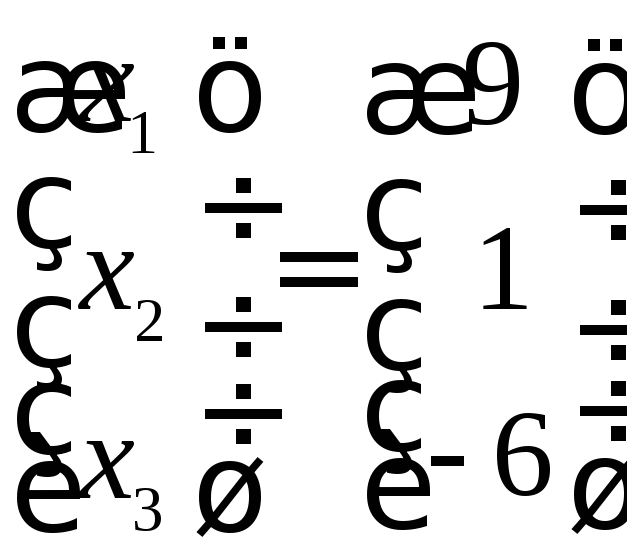Перевірка: .

Завдання 4. Розв’язати в цілих числах систему лінійних алгебраїчних рівнянь

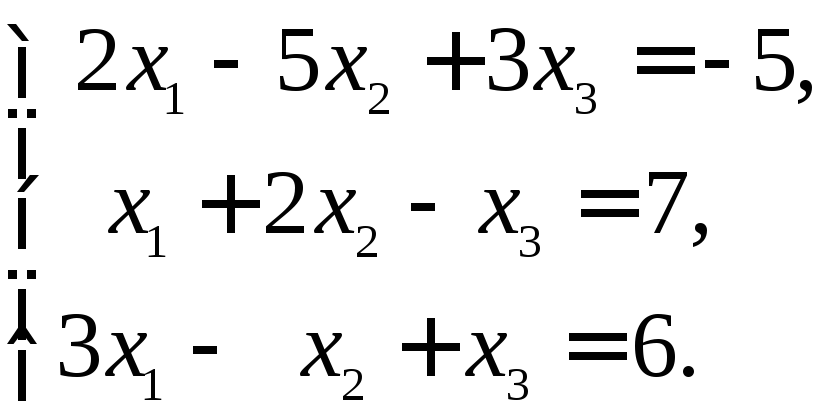
Розв’язання. Складемо матрицю

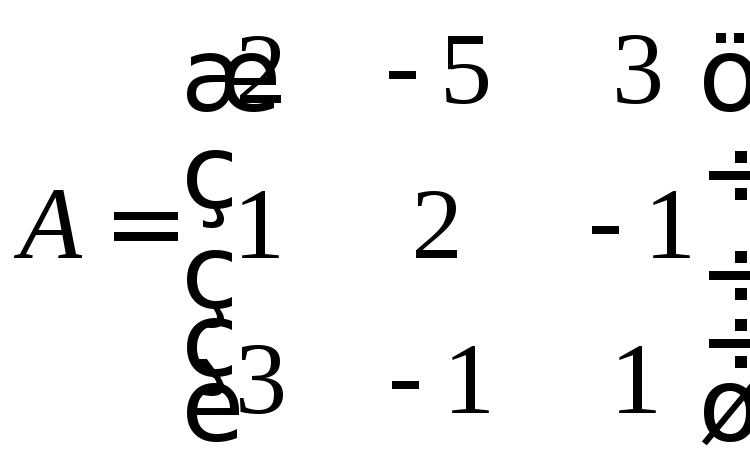
і матрицю розмірності, в якій під матрицеюстоїть одинична матриця розмірності:

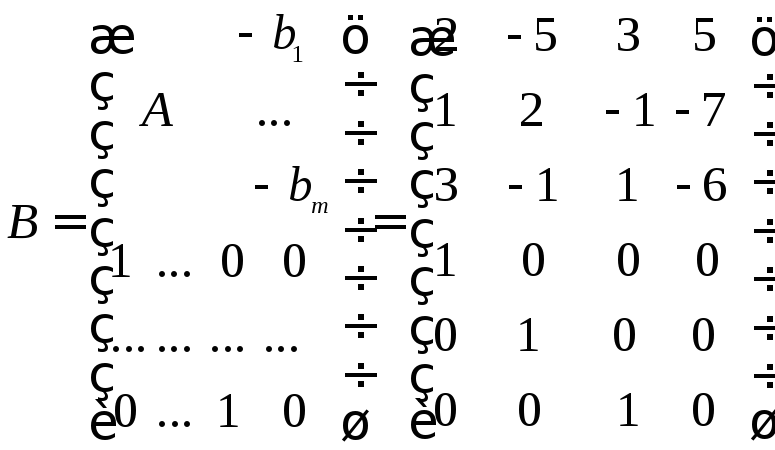
Перетворимо матрицю до частково-трикутного вигляду. Спочатку переставимо перший і другий рядки.

Вибираємо в першому рядку матриці найменший за абсолютною величиною ненульовий елемент . Йдучи за попереднім алгоритмом знаходження всіх цілочислових розв’язків лінійного алгебраїчного рівняння, будемо мати

Перетворимо матрицю :

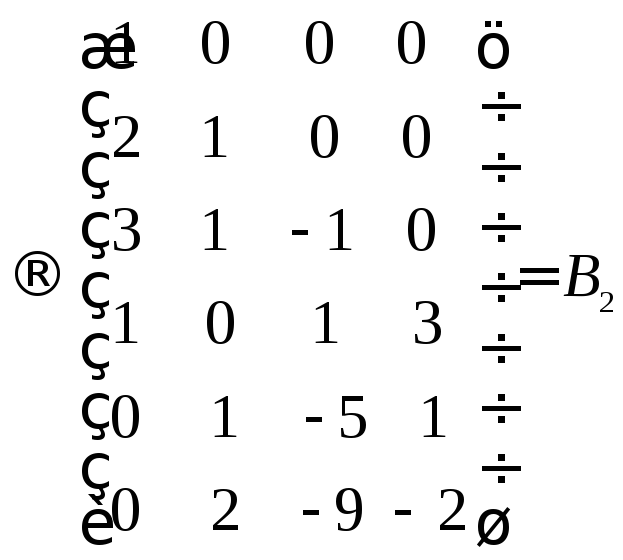
Загальний розв’язок системи в цілих числах має вигляд:

.
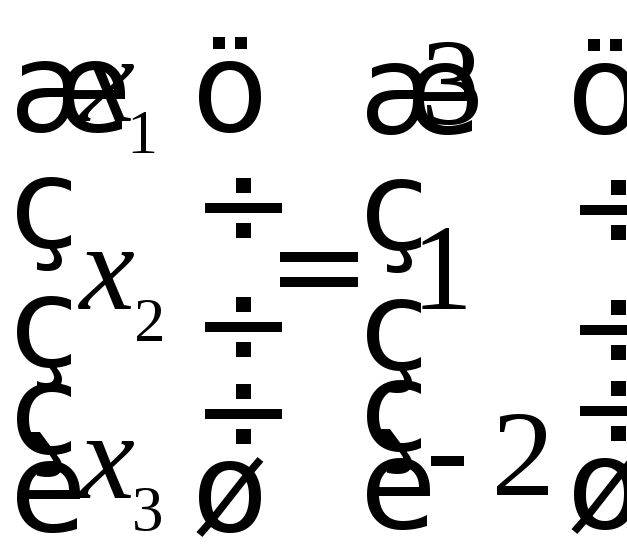