10. Определение нормы. Примеры нормированных векторных пространств над полем r.

Норма(обозначается ||x||) – такое число, поставленное в соответствие вектору х, для которого выполняются следующие свойства:

1. ||x||≥0, ||x||=0 только в том случае, если х=0

2. ||аx||=|a|*||x||

3. ||x+у||≤||x||+||у||

Пример:

Пространство R^m , на котором можно ввести несколько различных норм

11. Определение пространств c[0,1], cl[a,b], l1[a,b] со стандартной нормой.

С[a, b] – пространство непрерывных на [a, b] функций, где определена норма:

Следовательно в частности пространство C[0,1] – функции непрерывные на [0,1] с нормой

вероятно CL[a,b] это С^(к) [a,b] – пространство непрерывно дифференцируемых к раз функций с нормой:

Если в этом же пространстве ввести другую норму:

То получится пространство L_p[a,b] , его частный случай L₁[a,b] имеет стандартную норму:

12. Определение и примеры эквивалентных норм в нормированном векторном пространстве.

Пример: в

13. Определение и примеры банаховых пространств.

14. Сформулировать теорему «Принцип вложенных шаров».

Пусть в Банаховом пространстве X дана последовательность замкнутых шаров вложенных друг в друга причем . Тогда в Х существует единственная точка, принадлежащая всем шарам.

15. Сформулировать теорему «Принцип сжимающих отображений».

Пусть отображение f отображает замкнутое в банаховом пространстве E множество M в себя и является на M сжимающим с коэффициентом сжатия α. Тогда на множестве M отображение f имеет единственную неподвижную точку x*, которая может быть найдена методом последовательных приближений:

, n=1,2…

где (x)M и x_nx* при n. Кроме того, справедлива оценка скорости сходимости

16. Записать неравенства Гельдера и Минковского.

Пусть и – число, сопряжённое к нему (). Тогда для любых функций и , заданных на , для которых существуют интегралы

и

имеет место неравенство Гельдера

Пусть и пусть функции x(t) и y(t) таковы, что существуют и конечны интегралы , тогда справедливо неравенство Минковского

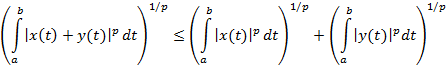
17. Определение пространства L_p[a,b].

Пространством называется нормированное векторное пространство, элементами которого являются классы эквивалентных между собой интегрируемых по Лебегу функций со степенью p и нормой

Сходимость в пространстве называется сходимостью в среднем со степенью p.

18. Определение и примеры открытых и замкнутых множеств в нормированных векторных пространствах.

19. Определение и примеры компактных и предкомпактных множеств в нормированных векторных пространствах.

20. Определение и примеры предгильбертовых и гильбертовых пространств. Определение пространств l₂ и L₂[a,b].

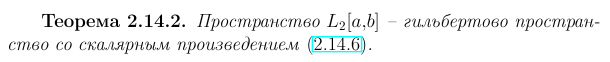
21. Определение нормы, согласованной со скалярным произведением, в гильбертовом пространстве.

22. Сформулировать теорему о проекции в гильбертовом пространстве.

Теорема(о проекции в Н)

Пусть Н - гильбертово пространство, L H – его замкнутое векторное подпространство. Для любого элемента существует единственная его проекция на подпространство L, т. е. .

23. Определение и примеры полных ортонормированных систем в пространстве L₂[-1,1].

Множество {x_a} ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением  такое, что (x_a, x_ab)=0 при . Если при этом норма каждого вектора равна единице, то система {x_a} наз. ортонормированной. Полная О. с. {x_a} наз. ортогональным (ортонормированным) базисом.

24. Определение и примеры ограниченных линейных операторов в НВП.

25. Определение и примеры вычисления нормы линейных ограниченных операторов.

26. Определение и примеры ограниченных линейных функционалов.

Пример:

27. Сформулировать теорему Рисса об общем виде ограниченного линейного функционала на гильбертовом пространстве.

Для любого линейного ограниченного функционала  на гильбертовом пространстве  существует единственный вектор  такой, что  для любого . При этом норма линейного функционала совпадает с нормой вектора :

. Теорема также означает, что пространство всех линейных ограниченных функционалов над изоморфно пространству .

28. Сформулировать классическую теорему Хана-Банаха в случае нормированного векторного пространства над полем R.

29. Определение и примеры компактных линейных операторов в НВП.

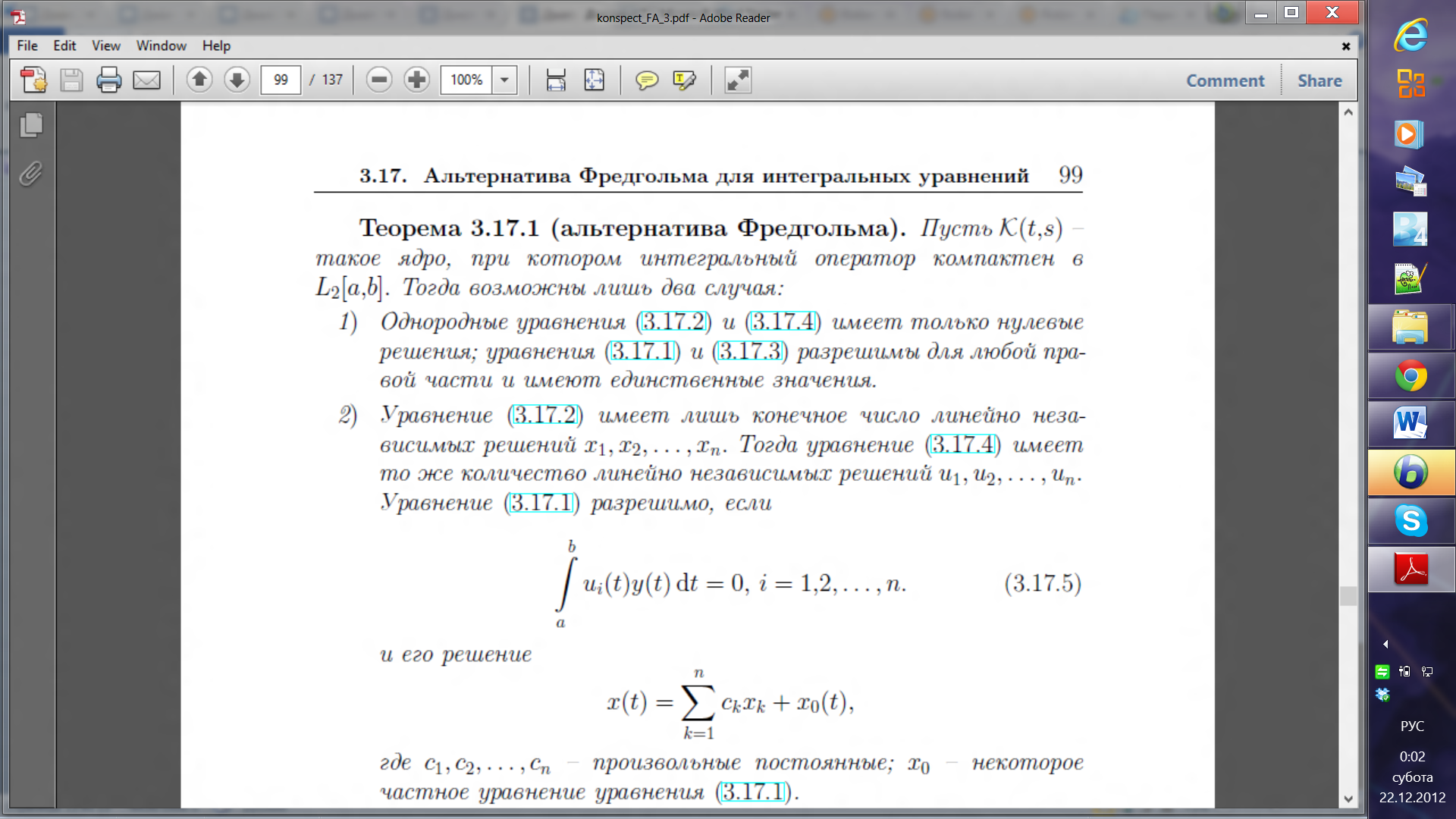
30. Сформулировать основную теорему Фредгольма для уравнений с интегральными операторами в пространстве L₂[a,b].