
- •Определение и пример кольца и алгебры. Определение и примеры мер на кольце.
- •Определение множества (ограниченного) на числовой прямой, измеримого по Лебегу. Примеры измеримых по Лебегу множеств на прямой.
- •Конструкция множества Кантора, его свойства. Классическое построение
- •Свойства
- •Определение и примеры измеримых функций.
- •Определение и примеры простых функций.
- •Определение интеграла Лебега для простой функции. Примеры интегрируемых и не интегрируемых по Лебегу простых функций.
- •Определение интегрируемой по Лебегу измеримой функции. Примеры интегрируемых и не интегрируемых по Лебегу функций.
- •Сформулировать теорему о связи интеграла Римана и интеграла Лебега для ограниченной функции, заданной на отрезке.
- •Определение и примеры векторных пространств над полем r, в том числе бесконечномерных.
- •Определение нормы. Примеры нормированных векторных пространств над полем r.
- •Определение пространств c[0,1], cl[a,b], l1[a,b] со стандартной нормой.
ОТВЕТЫ!
Минимум понятий, примеров, определений, теорем по курсу
«Функциональный анализ и интегральные уравнения»
-
Определение и пример кольца и алгебры. Определение и примеры мер на кольце.
Определение.
Пусть
задано некоторое непустое множество
Х.
Непустое семейство
![]() называется кольцом,
если оно обладает тем свойством, что из
А
называется кольцом,
если оно обладает тем свойством, что из
А![]() K
и В
K
и В![]() K
следует А
K
следует А![]() В
В![]() K,
АВ
K,
АВ![]() K.
K.
Определение.
Кольцо
K
называется алгеброй,
если Х![]() K.
Х
в этом случае называется единицей
кольца. Примеры:
K.
Х
в этом случае называется единицей
кольца. Примеры:
-
Для любого множества X система P(X) всех его подмножеств представляет собой алгебру множеств.
-
На числовой прямой R система его конечных и счетных подмножеств представляет собой кольцо, но не алгебру.
Определение.
Пусть
на некотором множестве Х
задано полукольцо S![]() Р(Х).
Будем говорить, что на S
задана мера,
если каждому элементу А
Р(Х).
Будем говорить, что на S
задана мера,
если каждому элементу А![]() S
поставлено в соответствие вещественное
число m(A)
S
поставлено в соответствие вещественное
число m(A)![]() R
таким образом, что выполнены следующие
условия:
R
таким образом, что выполнены следующие
условия:
1)
![]() A
A![]() S
: m(A)
S
: m(A)
![]() 0;
0;
2) если
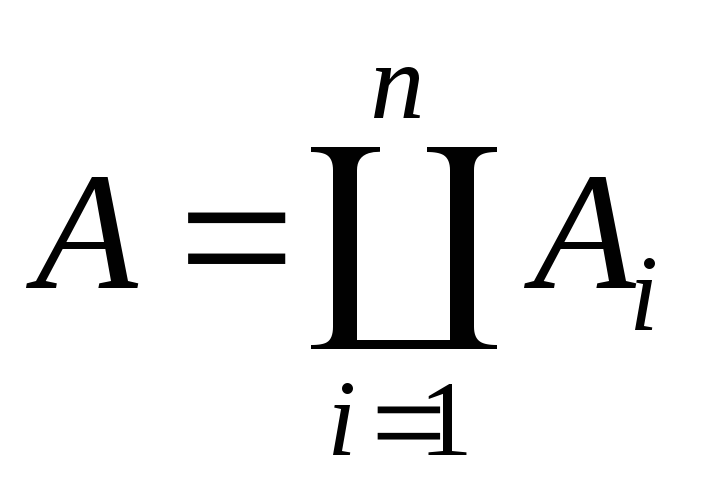 ,
A, Ai
,
A, Ai![]() S,
то
S,
то
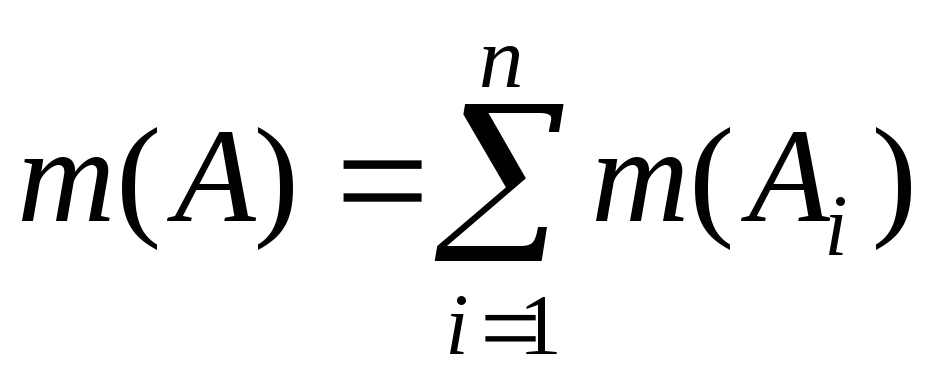 .
.
Определение.
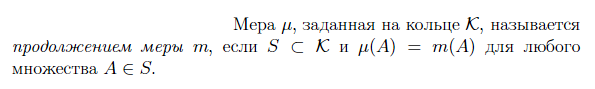 Свойства
меры на кольце
Свойства
меры на кольце
-
монотонность меры. Если А, В
 K
и А
K
и А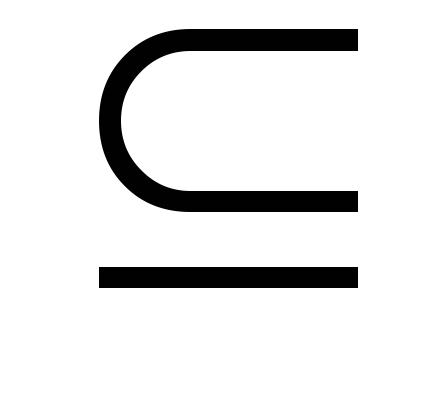 В,
то m(A)
В,
то m(A)
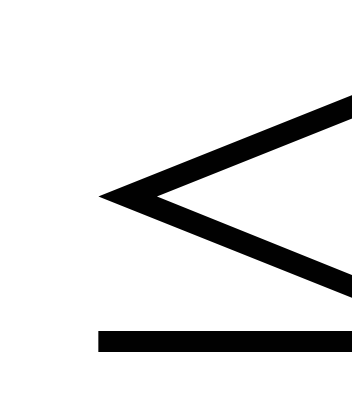 m(B);
m(B); -
если А, В
 К
и А
В,
то m(B\A)
= m(B)-m(A);
К
и А
В,
то m(B\A)
= m(B)-m(A); -
если А, В
 K,
то m(AB)
= m(A)+m(B)-m(AB);
K,
то m(AB)
= m(A)+m(B)-m(AB); -
если А, В
 K,
то m(A
K,
то m(A B)
=m(A)+m(B)-2m(AB);
B)
=m(A)+m(B)-2m(AB); -
для любых множеств А, В
 K
выполняется |m(A)-m(B)|
K
выполняется |m(A)-m(B)|
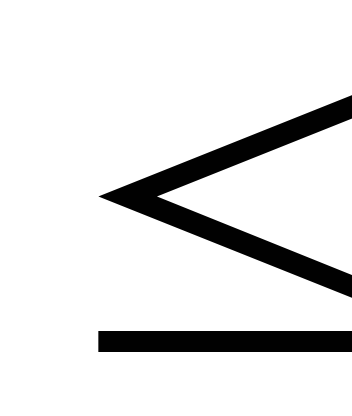 m(A
m(A B);
B); -
для любых множеств А, В, С
 K имеет место
следующее неравенство: m
(A
K имеет место
следующее неравенство: m
(A B)
B)
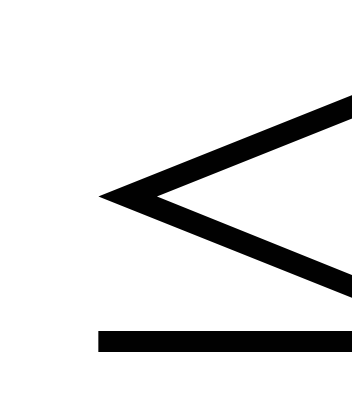 m(A
m(A C)+m(C
C)+m(C B).
B).

-
Определение множества (ограниченного) на числовой прямой, измеримого по Лебегу. Примеры измеримых по Лебегу множеств на прямой.
Пусть m
– полная, счётно-аддитивная, конечная
мера. Множество
![]() называется
измеримым по Лебегу
относительно меры m,
заданной на алгебре множеств К,
если выполняется равенство:
называется
измеримым по Лебегу
относительно меры m,
заданной на алгебре множеств К,
если выполняется равенство:
![]()
Пусть
![]() – некоторый фиксированный полуинтервал
прямой,
– некоторый фиксированный полуинтервал
прямой,
![]() – полукольцо, состоящее
из полуинтервалов
– полукольцо, состоящее
из полуинтервалов
![]() .
Пусть K
– алгебра подмножеств, порождённая
полукольцом S,
каждый элемент которой имеет вид
.
Пусть K
– алгебра подмножеств, порождённая
полукольцом S,
каждый элемент которой имеет вид
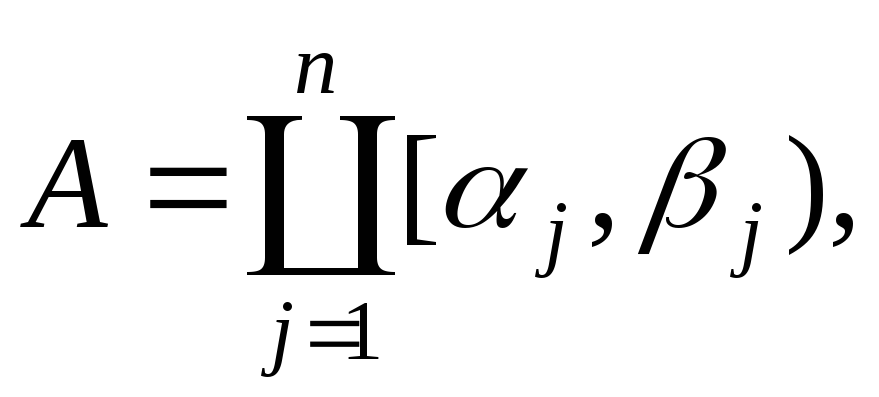 причём полуинтервалы в правой части
попарно не пересекаются. Через m
обозначим меру на алгебре K,
полученную продолжением меры с полукольца,
т.е.
причём полуинтервалы в правой части
попарно не пересекаются. Через m
обозначим меру на алгебре K,
полученную продолжением меры с полукольца,
т.е.
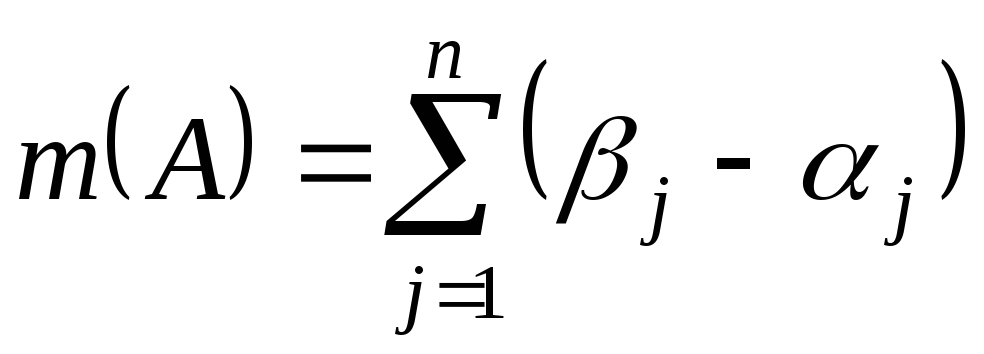 .
Для произвольного множества
.
Для произвольного множества
![]() определим внешнюю меру
определим внешнюю меру
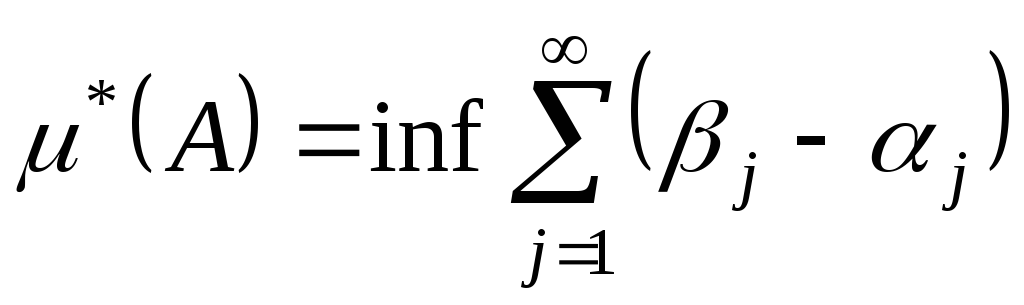 ,
где точная нижняя грань берётся по всем
таким наборам полуинтервалов
,
где точная нижняя грань берётся по всем
таким наборам полуинтервалов
![]() ,
что
,
что
![]() .
Множество
.
Множество
![]() называется измеримым по Лебегу,
если
называется измеримым по Лебегу,
если
![]() Таким образом, мерой Лебега
на отрезке называется лебеговское
продолжение длины.
Таким образом, мерой Лебега
на отрезке называется лебеговское
продолжение длины.
Примеры:
Рассмотрим измеримые по Лебегу линейные ограниченные множества:
-
множество, состоящее из одной точки, измеримо и его мера равна нулю;
-
всякое не более чем счётное ограниченное множество точек прямой измеримо и его мера равна нулю;
-
любой промежуток измерим и его мера равна его длине;
-
любое ограниченное открытое или замкнутое множество измеримо по Лебегу;
-
любое ограниченное борелевское множество на прямой измеримо по Лебегу.
-
Конструкция множества Кантора, его свойства. Классическое построение
Из единичного отрезка
С0=[0,1] удалим
среднюю треть, т. е. интервал (1/3,2/3).
Оставшееся точечное множество обозначим
через C1.
Множество C1=[0,1/3]![]() [2/3,1]состоит
из двух отрезков; удалим теперь из
каждого отрезка его среднюю треть, и
оставшееся множество обозначим через C2.
Повторив эту процедуру опять, удаляя
средние трети у всех четырёх отрезков,
получаем C3.
Дальше таким же образом получаем C4,C5
и тд. Обозначим через С пересечение
всех Сi.
Множество С называется
Канторовым множеством.
[2/3,1]состоит
из двух отрезков; удалим теперь из
каждого отрезка его среднюю треть, и
оставшееся множество обозначим через C2.
Повторив эту процедуру опять, удаляя
средние трети у всех четырёх отрезков,
получаем C3.
Дальше таким же образом получаем C4,C5
и тд. Обозначим через С пересечение
всех Сi.
Множество С называется
Канторовым множеством.
