МТФР_EK_дневная / Электронные лекции МТФР / мат теория фин рисков / Глава 2_Экономические риски / 4. Вывод Мертона

4. Вывод Мертона

Рассмотрим случай европейского опциона при следующих предположениях:

1. рынок «невязкий», т.е. нет никаких издержек на совершение сделок, торговля осущ. непрерывно, без ограничений допускаются займы и короткие продажи, ставки займов и ссуд одинаковые;

2. динамика цены акции, т.е. мгновенный доход на обыкновенную акцию описывается стох. дифф. ур-нием:

где – мгновенная ожидаемая доходность на обыкновенную акцию,

– мгновенная дисперсия доходности,

– стандартный Винеровский процесс,

– цена акции;

3. Динамика цены облигации, т.е. динамика доходности облигации описывается стох. дифф ур-нием:

где – мгновенная ожидаемая доходность,

– дисперсия доходности,

– станд. Винеровский процесс до срока погашения ;

4. предпочтения инвесторов; не нужно никаких предположений о предпочтениях инвесторов кроме того, чтобы цена опциона определялась так, чтобы не было доминирующих ценных бумаг.

( доминирует над , если в некот. известную дату в будущем доходность будет превышать доходность в некот. состоянии среды и будет такой же, как доходность во всех остальных состояниях среды)

Кроме того, все инвесторы согласны со значениями и , и с характеристиками распределений и .

Предположим, что цена опциона явл. функцией от цены акции, цены облигации и срока до истечения контракта, т.е. .

Т.е. при заданных предположениях о распределении и можно вывести по формуле ИТО, что изменение цены опциона удовл. следующему стох. дифф. ур-нию:

(*)

где – частные производные по соответствующим переменным.

Кроме того,

,

где – мгновенный коэффициент корреляции между доходностями на акцию и на облигацию.

Рассмотрим портфель, содержащий обыкновенную акцию, опцион и облигацию со сроком погашения , равному сроку истечения опциона.

Пусть совокупная инвестиция в портфеле равна .

Пусть – мгновенное количество денег в портфеле, инвестированных в обыкновенную акцию;

– --//-- в опцион;

– --//-- в облигацию.

Тогда условие нулевой совокупной инвестиции: .

Если явл. мгновенной доходностью портфеля, то можно записать:

где

Два портфельных условия и условия равновесия приводят к системе дифф. ур-ний:

Эта система имеет ненулевое решение , когда:

(1)

Тогда, с учётом (1), то согласно определению и ур-нию (*) подразумевается, что

или

Значит, исходя из последней записи и (1), ур-ние (*) можно переписать в виде:

(2)

которое является дифф. ур-нием в частных производных параболического типа второго порядка.

Если – стоимость европейского опциона, тогда оно должно удовлетворять ур-нию (2) с граничными условиями:

, т.к. .

Окончательно можно получить цену любого европейского опциона:

(**)

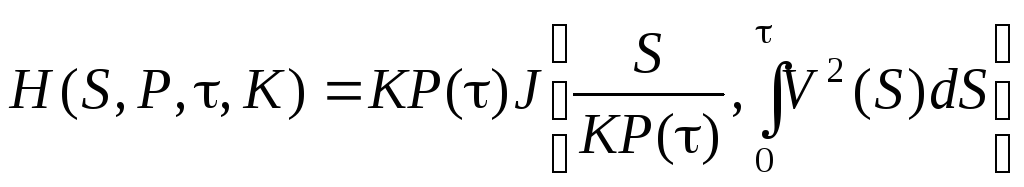Действительно, введём переменную , которая является ценой на долю акционерного капитала на дату истечения опциона.

Согласно формуле ИТО, динамика переменной описывается стохастическим дифф. ур-нием:

Из этого уравнения мгновенная дисперсия доходности инвестиций будет равно

.

Введем переменную

,

где не зависит от и является ценой опциона и измеряется в тех же единицах, что и .

Подстановка вместо в (2) и (3) приведет к уравнению в частных производных для :

(4)

Следовательно, является функцией от и .

Рассмотрим новую временную переменную .

Определим ф-цию и подставим её в (4).

Получается: 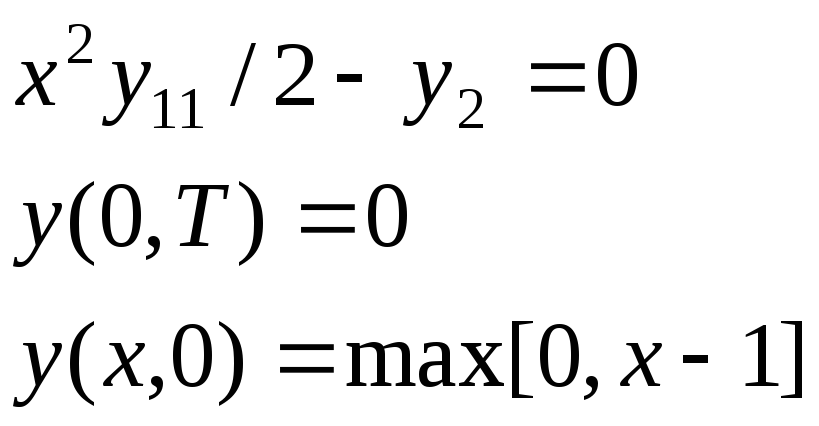(5)

Как только мы решим ур-ние (5), то мы получим цену любого европейского опциона (**).