МТФР_EK_дневная / Электронные лекции МТФР / мат теория фин рисков / Глава 2_Экономические риски / 3. Определение цен опционов. Модель Бяэка-Шоулся

3. Определение цен опционов. Модель Бяэка-Шоулса.

Составляется безрисковый портфель, содержащий позиции в двух финансовых контрактах: финансовой производной и акции.

Затем доход портфеля приравнивается к доходу, получаемому от такой же, по величине инвестиции при безрисковой ставке. В модели Бяэка-Шоулса портфель остаётся безрисковым только в течение короткого периода времени.

Перечислим предположения, лежащие в основе анализа:

1. Торговля активами производится в непрерывном времени;

2. Безрисковая процентная ставка 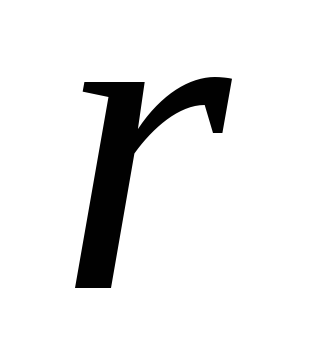явл. постоянной и одинаковой для всех сроков погашения;

3. Цена актива изменяется во времени случайно, образуя случайный процесс, кот. удовлетворяет стохастическому дифф. уравнению

где и явл. const.

4. Не имеется никаких безрисковых арбитражных возможностей;

5. Разрешается короткая продажа активов с использованием выручки в полном объёме, т.е. активы и их финансовые производные свободно продаются и покупаются без ограничений;

6. Не имеется каких-либо расходов на совершение сделок и налоги. Могут продаваться (покупаться) какие угодно доли всех активов;

7. В течение срока действия финансовых производных никакие дивиденды не выплачиваются.

При этих предположениях удаётся доказать, что стоимость финансовой производной будет зависеть от цены актива , времени и от параметров, которые считаются известными константами.

Тогда поскольку цена актива – СП, цена финансовой производной сама является СП, который удовлетворяет стох. дифф. ур-нию, определяемому по формуле ИТО:

.

Разностная версия имеет вид:

где и – изменения цен и через короткий временной интервал .

Далее можно получить дифф. ур-ние Блэка-Шоулса для цены финансовой производной:

.

Рассмотрим call-опцион европейского типа с ценой исполнения и датой исполнения на лежащей в основе актив стоимостью .

Владелец этого опциона в дату имеет право купить одну лежащую в основе контракта акцию по цене у продавца опциона. Владелец опциона никоим образом не обязан покупать эту акцию. Право купить одну лежащую в основе контракта акцию по цене распространяется только на дату . Отсюда следует, что опцион им. смысл исполнять только тогда, когда его стоимость будет неотрицательной, т.е. в дату стоимость опциона будет равна

Это равенство следует рассматривать как граничное условие при решении ур-ния Блэка-Шоулса в случае европейского call-опциона.

Т.о., разнообразие финансовых производных задает разнообразие граничных условий и, , формул для определения цен этих финансовых производных.

Получим знаменитую формулу Блэка-Шоулса определения стоимости европейского call-опциона.

Для этого необх. решить ур-ние при граничном условии

.

Получим: , (1)

где – функция стандартного нормального распределения, а , – определяются формулами:

Стоимость европейского put-опциона находим аналогично.

В этом случае нам нужно решить ур-ние Блэка-Шоулса при граничном условии

.

В этом случае получим:

Т.о., разработанная Блэком и Шоулсом модель особенно привлекательна тем, что она базируется на общей равновесной постановке задачи и её конечная формула явл. ф-цией «наблюдаемых» переменных.

Особенность формулы (1) в том, что она не зависит от ряда параметров. Цена опциона не зависит от ожидаемой доходности на обыкновенную акцию, предпочтений инвесторов или средней массы активов. Это важный результат, поскольку ожидаемая доходность не наблюдается непосредственно, а оценки по прошлым данным обычно неточные из-за нестац-ти.

Это также подразумевает, что попытки использовать цену опциона ожидаемой доходности акции или рисковых предпочтений инвесторов приводят к ошибкам.

Цена опциона зависит от процентный ставки («наблюдаемой») и полной дисперсии доходности на обыкновенную акцию, которая часто явл. стабильным параметром и, , может быть точно оценена из временных рядов данных.