
- •2. Операции над множествами. Отображение множеств
- •5. Лемма о вложенных отрезках.
- •6. Лемма о конечном покрытии.
- •8. Предел числовой последовательности и общие свойства предела
- •9. Предельный переход и арифметические операции
- •12. Существование предела монотонной ограниченной последовательности
- •13. Подпоследовательность. Теорема Больцано-Вейерштрасса о выделении сходящейся подпоследовательности.
- •14 Предел функции. Эквивалентность определений по Коши и по Гейне.
- •16 Предел функции и неравенства.
- •17 Односторонние пределы
- •18.Предел. Отнош. Синуса. К. Аргумент.
- •21 Непрерывность ф-ции в точке.
- •22 Точки разрыва функции.
- •24 Огранниченность ф-ции непрер. На отрезке.
- •28. Равномерная непрерывность функций
- •29.Непр. Элементарн.Ф-ций.
- •31.Непрерывность ф-ции, имеющей производную.
- •38. Теорема Ферма.
- •40. Теорема Лагранжа
- •44.Формула Тейлора. Остаточный член ф форме Пеано
- •48. Выпуклость функции
- •49. Tочки перегиба
16 Предел функции и неравенства.
Теорема 11. Пусть f : X → Y , f(X) = Y , g : Y → R и limf(x) = y0, x→x0, limg(y) = c. Если существует проколотая окрестность V˙ (x0) точки x0, что f(x) =/ y0 ∀x ∈ V˙ (x0), то limϕ(x) = limg(f(x))= c. x→x0
Доказательство. Имеем (limf(x) = y0)⇔ (∀U(y0) ∃V˙ (x0) ⊂ X : ∀x ∈ V˙ (x0) ⇒ f(x) ∈ U(y0))
Так как по условию f(x) =/ y0 в некоторой V˙ (x0), то
∀U˙ (y0) ∃V˙ (x0) ⊂ X : ∀x ∈ V˙ (x0) ⇒ f(x) ∈ U˙ (y0).
Так же имеем (limg(y) = c, y→y0)⇔(∀V (c) ∃U˙ (y0) ⊂ Y : ∀y ∈ U˙ (y0) ⇒ g(y) ∈ V (c))
Тогда в итоге
∀V (c) ∃V˙ (x0) ⊂ X : ∀x ∈ V˙ (x0) ⇒ g(f(x))∈ V (c).
17 Односторонние пределы
Определение 5. Число y0 называется левосторонним пределом функции y = f(x) в точке x0, если для любого ε > 0
существует δ > 0, такое, что ∀x ∈ V˙δ(x0 − 0) ⇒ |f(x) − y0| < ε и обозначается limf(x) = y0, x→x0−0
Определение 6. Число y0 называется правосторонним пределом функции y = f(x) в точке x0, если для любого ε > 0
существует δ > 0, такое, что ∀x ∈ V˙δ(x0 + 0) ⇒ |f(x) − y0| < ε и обозначается limf(x) = y0, x→x0+0
Теорема 12. Чтобы функция f(x) в точке x0 имела предел, необходимо и достаточно, чтобы она имела оба одно-
сторонних предела равных между собой. Тогда общее значение этих односторонних пределов равно пределу функции
f(x) в точке x0.
18.Предел. Отнош. Синуса. К. Аргумент.
Докажем,
что
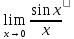 Так как f(x) =
Так как f(x) =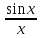 является четной функцией, то рассмотрим
ее только на интервале (0;
является четной функцией, то рассмотрим
ее только на интервале (0;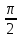 ) Возьмем дугу AM единичного круга,
соответствующую углу, радианная мера
которого равна x. Площадь сектора OAM
заключена между площадями треугольников
OMA и OTA: S
) Возьмем дугу AM единичного круга,
соответствующую углу, радианная мера
которого равна x. Площадь сектора OAM
заключена между площадями треугольников
OMA и OTA: S OMA
< Sсек < S4OAT⇔
OMA
< Sсек < S4OAT⇔
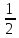 ·
|OA| · |PM| <
·
|OA| · |PM| <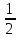 ·
|OA|2·
x <
·
|OA|2·
x <
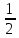 ·
|OA| · |AT|. Так как |OA| = 1, |MP| = sin x, |AT| = tg x, тоsin
x
< x
< tg
x
⇔
1 <
·
|OA| · |AT|. Так как |OA| = 1, |MP| = sin x, |AT| = tg x, тоsin
x
< x
< tg
x
⇔
1 <
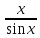 ·<
·<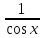 ⇔
cos
x
<
⇔
cos
x
<
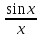 <
1. В силу четности функцииcos
x
и
<
1. В силу четности функцииcos
x
и
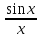 последнее двойное неравенство справедливо
и для интервала ( -
последнее двойное неравенство справедливо
и для интервала ( -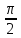 ; 0). Таким образом, для любого x∈(
-
; 0). Таким образом, для любого x∈(
-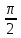 ; 0) ∪(0;
; 0) ∪(0;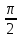 ) выполняется
неравенство cos
x
<
) выполняется
неравенство cos
x
<
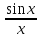 <
1 Переходя
к пределу при
<
1 Переходя
к пределу при
x
→ 0 получим 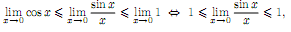
т.е.
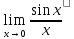 =1 – который называют первым замечательным
пределом.
=1 – который называют первым замечательным
пределом.
19 Число е.
Пример 1. Доказать справедливость неравенства (неравенство Я. Бернулли)
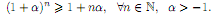
Решение. Докажем, основываясь на методе математической индукции.
1. При n = 1 утверждение, очевидно, справедливо. 2. Предположим, что оно справедливо при n = k, т.е. верно (1 + α) k > 1 + kα.
3.
Докажем, что оно справедливо при n =
k+1.Действительно
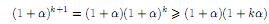
![]()
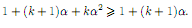 Согласно
методу математической индукции заключаем,
что утверждение справедливо∀n
∈
N. Рассмотрим
последовательность {xn},
где
Согласно
методу математической индукции заключаем,
что утверждение справедливо∀n
∈
N. Рассмотрим
последовательность {xn},
где
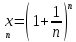 Покажем,
что последовательность {yn},
где
Покажем,
что последовательность {yn},
где
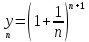 убывающая.
Действительно∀n
убывающая.
Действительно∀n
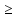 2, находим
2, находим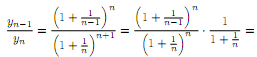
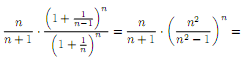
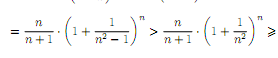
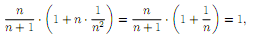
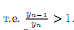 Очевидно,
что все члены последова-тельности {yn}
имеют положительные члены, а следова-тельно,
согласно теореме Вейерштрасса, она
имеет предел. Тогда
Очевидно,
что все члены последова-тельности {yn}
имеют положительные члены, а следова-тельно,
согласно теореме Вейерштрасса, она
имеет предел. Тогда 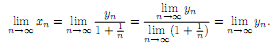
Определение
1.
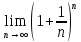 =е
=е
20Бесконечно малые и бесконечно большие функции. Символы ~, о, О. Сравнение функций.
Определение 1. Функция f(x) называется бесконечно малой функцией (или бесконечно малой) при x → x0 если limf(x) = 0.
Определение 2. Функция f(x) называется бесконечно большой функцией (или бесконечно большой) при x → x0 если limf(x) = ∞.
Бесконечно малые функции принято обозначать строчными буквами греческого алфавита α, β, γ,...
Теорема 13.
Если функция f(x) при x → x0 – бесконечно большая, то функция 1/f(x) при x → x0 – бесконечно малая.
Если функция f(x) при x → x0 – бесконечно малая, то функция 1/f(x) при x → x0 – бесконечно большая.
