49. Tочки перегиба
Определение 3. Точка x0 называется точкой перегиба функции f(x), если при переходе через точку x0 функция
меняет характер выпуклости.
Теорема 20 (необходимое условие точки перегиба). Если функция f(x) имеет непрерывную в точке x0 произ-
водную f’’(x) и x0 – точка перегиба, то f’’(x0) = 0.
Доказательство. Если бы в точке перегиба x0 выполнялось неравенство f’’(x0) > 0 или f’’(x0) < 0, то в силу непрерывности f’’(x) существовала бы окрестность точки x0, в которой f’’(x) > 0 или f’’(x) < 0. По теореме 19 в этой окрестности функция была бы выпукла вниз или вверх соответственно, что противоречит наличию перегиба в точке x0.
Из теоремы 20 следует, что точками возможного перегиба функции f(x) могут быть точки x0 в которых f’’(x0) = 0, либо точки, в которых f’’(x) не существует, в частности она бесконечна.
Теорема 21 (первое достаточное условие перегиба). Если функция f(x) дважды непрерывно дифференцируема в
окрестности точки x0 и при переходе через точку x0 производная f’’(x) меняет знак, то точка x0 является точкой
перегиба функции f(x).
Доказательство. Пусть, к примеру, f’’(x) > 0 при x < x0 и f’’(x)<0 при x>x0. Тогда по теореме 19 функция f(x) выпукла вниз на интервале (x; x0) и выпукла вверх на интервале (x0; x), т.е. x0 – точка перегиба.
Теорема 22 (общее достаточное условие перегиба). Пусть в точке x0 для функции f(x) выполнены условия
f’’(x0) = f’’’(x0) = . . . = f(n−1) (x0) = 0
и в точке x0 существует непрерывная производная f (x0), n > 2, причём f (x0) = 0. Если n – нечётное число, то
в точке x0 функция f(x) имеет перегиб.
Доказательство. Разлагая f(x) по формуле Тейлора n−1-го порядка с учетом условия получаем
f(x)
= f(x0)
+ f’(x0)(x
− x0)
+
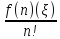(x
− x0)n,
(5.32)
где ξ расположена между x0 и x.
Если Y (x) = f(x0) + f’(x0)(x − x0) уравнение касательной к графику функции f(x) в точке (x0, f(x0)), то из (5.32) имеем
f(x)
− Y
(x)
=
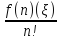(x
− x0)n,
(5.33) где n
– нечётное.
В силу непрерывности f(n)(x) в точке x0 существует окрестность этой точки, в которой производная f(n)(x) сохраняет знак, совпадающий со знаком f(n)(x0). Поэтому можем считать, что знаки f(n)(x0) и f(n)(ξ) совпадают. Тогда из равенства (5.33) получаем, что при переходе x через x0 слева направо график функции располагается по разные стороны от касательной, т.е. в точке (x0, f(x0)) имеется перегиб.