4. Індуктивність у колі змінного струму

Якщо в провідному контурі тече струм силою І, то такий струм створює магнітне поле і площу контуру пронизує магнітний потікФ, який пропорційний силі струму в цьому контурі

, (54.13)

де коефіцієнтом пропорційності є величина L, яка називається індуктивністю і вимірюється в Гн (генрі¹), так, що 1 Гн = 1 Вб/А.

При зміні струму на dI магнітний потік змінюється наdФ

, (54.14)

тоді згідно закону електромагнітної індукції

, (54.15)

в цьому контурі виникає ЕРС, яка отримала назву ЕРС самоіндукції

. (54.16)

З (54.16) випливає, що , тобто 1 Гн індуктивність такого контуру в якому при зміні сили струму з швидкістю 1 А/с виникає ЕРС самоіндукції 1 В.

Якщо в колі змінного струму знаходиться індуктивністьL, наприклад, соленоїд (рис.54.5), то внаслідок явища самоіндукції коливання сили струму не будуть співпадати по фазі з коливаннями напруги. Дійсно, збільшенню струму в соленоїді перешкоджає ЕРС самоіндукції, внаслідок чого сила струму досягає максимального значення пізніше в порівнянні з максимальним значенням напруги.

Таким чином струм в колі з індуктивністю зумовлений дією прикладеної змінної напруги Uта ЕРС самоіндукціїі закон Ома для такого кола прийме вигляд:

. (54.17)

Розглянемо коло, де активний опір відсутній (R=0), тоді

, (54.18)

враховуючи (54.16) отримаємо

. (54.19)

Нехай струм в колі змінюється за законом

, (54.20)

Взявши похідну згідно (54.14) будемо мати

, (54.21)

і порівнюючи з (54.20) бачимо, що коливання сили струму відстають за фазою на /2, що можна зобразити векторною діаграмою

В (54.21) величинавизначає максимальне (амплітудне) значення напруги

. (54.22)

Порівнюючи цей вираз із законом Ома U=IR легко бачити, що величинаL грає роль опору, який називається індуктивним реактивним опором

. (54.23)

5. Активний опір, індуктивність та ємність у колі змінного струму

В електричних колах можуть бути одночасно активні та реактивні опори. На рис.54.7 наведена схема послідовного з’єднання активного опору R, індуктивностіLта ємності (конденсатора)С.

Враховуючи фазові співвідношення між коливаннями сили струму і напруги на кожному елементі такого кола, векторна діаграма кола буде мати вигляд (54.8), деU_R– максимальна напруга на активному опорі,U_L– на індуктивності,U_C– на ємності,I_o– максимальне значення струму, однакове для всіх ділянок. Виконавши векторне додавання напруг, будемо мати, що модуль результуючої напруги дорівнює

, (54.24)

враховуючи (54.11) та (54.22) одержимо

, (54.25)

або

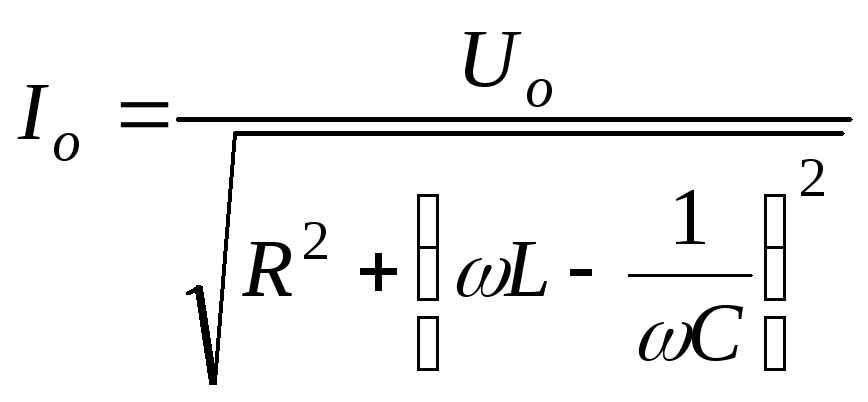, (54.26)

Отриманий вираз називають законом Ома для кола змінного струму, а величину

, (54.27)

називають повним опором, або імпедансом (від грецького – „повний”).

6. Принцип експериментального визначення ємності конденсатора методом вимірювання його реактивного опору.

Якщо в колі змінного струму знаходиться тільки ємнісний опір (конденсатор), то з (54.26) отримаємо (54.28). Виміривши ефективні значення напруги та струму в колі, яке містить конденсатор, за формулою (54.28) можна підрахувати ємнісний опір конденсатора, а виміривши частоту змінного струму ν і враховуючи, що ω=2πν, отримаємо вираз (54.29) для розрахунку ємності конденсатора.

(54.28)

(54.29)

Таким чином, принцип даного експериментального методу визначення ємності конденсатора базується на вимірюванні його реактивного опору в колі змінного струму.