введение в тфп

которые образуют соответствующее силовое поле. Например, электромагнитное взаимодействие осуществляется обменом фотонами, слабое взаи-

модействие − обменом промежуточными векторными бозонами и т.д. Объ- ектно-материальный контекст понятия «поле» отражает в познании принцип близкодействия материальных тел.

Формально-математическое содержание термина «поле». Материальное поле имеет те или иные характеристики, выражаемые

количественно физическими величинами. В формально-математическом контексте под термином «поле» подразумевается физическая величина, зависящая от положения в пространстве и времени. Таким образом, в фор- мально-математическом контексте речь идет о поле физической величины.

Например, можно ввести понятие температурного поля T(x, y, z; t). Функция T(x, y, z; t) показывает, что температура разных точек тела в общем случае является функцией координат этих точек и времени.

При описании электромагнитного поля как материального объекта вводится поле вектора напряженности электрического поля E = E(x, y, z; t), поле вектора индукции магнитного поля В = В(x, y, z; t), поле вектора поляризованности Р(x, y, z; t), вектора намагниченности магнетика J(x, y, z; t),

поле диэлектрической восприимчивости χэ(x, y, z); поле магнитной вос-

приимчивости χм(x, y, z) и т.д.

В среде, в которой распространяется акустическая волна, можно ввести поле упругих напряжений в среде, поле смещения частиц среды и т.д.

Скалярные и векторные поля от векторного аргумента.

Если физическая величина скаляр, то поле такой величины в фор- мально-математическом смысле называют скалярным полем; если величи-

на вектор, то − векторным полем.

Скалярное поле характеризуется единственным числом - скалярной величиной. Поле потенциала ϕ(r) электростатического поля является при-

мерами скалярного поля от векторного аргумента − радиус-вектора r точки пространства, в которой скалярное поле приобретает некоторое значение. В координатном представлении скалярное поле сводится к функции

от координат ϕ(x, y, z).

Поле вектора напряженности электрического поля E(r) является примерами векторного поля от векторного аргумента. В координатном представлении векторное поле сводится к трем скалярным функциям. Например, поле вектора напряженности электрического поля E(r) сводится

к функциям Ex(x, y, z), Ey(x, y, z), Ez(x, y, z).

Неизменное во времени поле называется стационарным, если поле изменяется с течением времени, то поле называется нестационарным. Нестационарность выражается включением времени t в набор аргументов функции: E(r, t). На рисунках скалярное поле можно представить в виде набора поверхностей одинакового уровня. Во всех точках поверхности

уровня, скалярная функция имеет одно и то же значение, т.е. поверхность

уровня характеризуется уравнением ϕ(x, y, z) = const. В разных физических теориях поверхности одинакового уровня называются по-разному: в электростатике поверхность одинакового потенциала называется эквипотенциальной поверхностью; поверхность одинаковой температуры называется изотермической поверхностью и т.д.

Векторное поле на рисунках обозначается векторными линиями, т.е. линиями, касательные к которым в каждой ее точке совпадают с направлением векторного поля в этих точках. Густота линий указывает относительное изменение модуля векторной величины в пространстве: чем гуще расположены линии, тем модуль вектора больше. Векторные линии в силовых полях (электрических, магнитных, гравитационных) обычно называют силовыми линиями. На рис. 11, в качестве примера, показаны изотермические поверхности температурного поля T(r) и линии векторного поля потока тепла q(r).

y 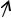q(x, y, z)

T4

T3

T2

0

T1 x

Рис. 11. Скалярное температурное поле T(x, y, z) представлено на рисунке изотермическими поверхностями Тi = const (показаны следы изотермических поверхностей при z = 0 в виде пунктирных линий). При Т1> Т2 >Т3 >Т4 возникает поток тепла q(x, y, z) в направлении от изотермы Т1 к Т4; q(x,y,z) – образует векторное поле. Векторные линии показаны сплошными линиями

1.8. Градиент потенциала электростатического поля

Введем понятие градиента потенциала электростатического поля. Рассмотрим две эквипотенциальные поверхности, потенциал которых ϕ1

и ϕ2 (рис.12). Исходя из смысла эквипотенциальной поверхности, разность потенциалов между эквипотенциальными поверхностями не зависит от выбора точек отсчета на поверхностях:

ϕС − ϕА = ϕВ − ϕА = ϕ2 − ϕ1 = Δϕ = const.

Рис. 12. К введению понятия градиента скалярного поля

в точке А в направлении вектора d l. «Скорость» изменения потенциала максимальная в перпендикулярном направлении к поверхности ϕ1. На рис.12 это направление обозначено вектором dh, где модуль вектора − отрезок dh− кратчайшее расстояние между плоскостями ϕ1 и (ϕ1 + dϕ). Отрезок dh перпендикулярен поверхности уровня ϕ1. Естественно, отрезок dh

перпендикулярен и поверхности (ϕ1 + dϕ), т.к. поверхности ϕ1 и (ϕ1 + dϕ) расположены бесконечно близко друг к другу. Градиентом скалярного по-

ля ϕ называется вектор, направленный в сторону быстрейшего изменения ϕ и равный производной по этому направлению:

где n = ddhh – единичный вектор в направлении dh. Итак, градиент как векторная величина характеризует наибыстрейшее пространственное изменение скалярной функции, а производная ddϕh называется производной

по направлению d h. Градиент как вектор можно представить векторной

суммой пространственных изменений потенциала ϕ по направлениям всех координатных осей. На рис.13 приведена иллюстрация представления градиента в декартовой системе в плоскости X0Y.

y

Таким образом, в координатном представлении градиент запишется в виде:

где: gradxϕ = ∂∂ϕx ; gradyϕ = ∂∂ϕy ; gradzϕ = ∂∂ϕz − проекции градиента на соответствующие оси декартовых координат.

Рассмотрим важную особенность градиента скалярного поля. Умножим скалярно градиент gradϕ на дифференциал радиус-вектора dr, получим:

∂∂ϕz d z есть полный дифференциал функции ϕ(x, y, z).

Итак, если имеется некоторый вектор b, такой, что для произвольного dr выполняется условие

( ϕ читается: градиент фи).

Приведем пример вычисления градиента.

Задача. Пусть скалярный потенциал выражается функцией ϕ ( r) = k 1r ,

где k – константа. Определить градиент потенциала этого поля.

Напомним, потенциал электростатического поля точечного заряда и гравитационного поля точечной гравитационной массы имеют именно такой вид (см. формулу 1.15).

Решение. Так как потенциал определяется только расстоянием от начала

отсчета до точки поля, то эквипотенциальные поверхности − это концентрические сферы с центром в начале отсчета. Нормаль к поверхности сферы совпа-

дает с радиус-вектором, поэтому модуль градиента равен: gradϕ = ddrϕ .

Сначала воспользуемся формулой (1.21). Имеем: ddrϕ = − k r12 . Градиент на-

правлен в сторону возрастания потенциала, т.е. при ddrϕ > 0 ортом градиента явля-

− k rr3 .

Этот же результат можно получить, используя формулу (1.22).

ddϕr = − k r12 . Аналогично по другим компонентам. Подставив производные потенциала по компонентам в (1.22), получим:

Полученное решение называют законом обратного квадрата. В электростатике – это закон Кулона, в ньютоновской теории гравитации – это закон всемирного тяготения.

1.9.Циркуляция электростатического поля

В§ 1.4 вычислена работа электростатического поля точечного заряда. На замкнутой траектории работа электростатического поля равна нулю

Из этого соотношения получаем выражение для циркуляции напряженности электростатического поля (напомним, циркуляцией называется криволинейный интеграл по замкнутой кривой – по контуру):

Если кривая, по которой берется интеграл, не замкнута (т.е. кривая не является контуром), то криволинейный интеграл равен убыли потенциала (− ϕ) при переходе из начальной в конечную точку кривой (из начальной точки электростатического поля в конечную точку):

1.10.Связь напряженности и потенциала электростатического поля

Основной (исходной) характеристикой электрического поля является напряженность поля E. Если векторное поле напряженности E(x, y, z),

неизвестно, но известно скалярное поле потенциала ϕ(x, y, z), то по полю скаляра ϕ можно восстановить поле вектора E.

Если dl в (1.27) направить вдоль оси 0X, то dl = idx. Скалярное произведение Edl примет вид:

Edl = E idx = Ex dx.

Сравнивая полученное соотношение с (1.27), получим:

Ex = − ∂∂ϕx .

Полученное выражение для Ex показывает, что проекция вектора напряженности электростатического поля E на направление оси 0X определяется убылью ( знак минус!) потенциала в этом направлении. Аналогичные выражения получим по другим осям:

Ey = − ∂∂ϕy , Ez = − ∂∂ϕz .

Таким образом, вектор E = Exi + Eyj + Ezk можно записать в виде

Выражение в скобках есть градиент потенциала электростатического поля (см. 1.24). Уравнение (1.28) кратко записывается в форме

Итак: Ex = −gradxϕ = − ∂∂ϕx ; Ey = −gradyϕ = − ∂∂ϕy ; Ez = −gradzϕ = − ∂∂ϕz .

Задача вычисления поля диполя. Задана система из близко расположенных на расстоянии l двух противоположных по знаку и равных по модулю зарядов

q+ и q−. Определить потенциал и напряженность поля этой системы зарядов. Напомним, такая система зарядов называется электрическим диполем, ха-

рактеризуемым вектором дипольного момента p = ql. Дипольный момент направлен от отрицательного заряда к положительному, и по модулю равен p = ql. Примером диполя является полярная молекула NaCl.

Решение. Потенциал двух точечных зарядов равен сумме потенциалов полей зарядов q+ и q−:

где r1 и r2 – расстояния от соответствующих зарядов до рассматриваемой точки A поля с координатами ( x, y, z). Так как r1>> l и r2 >> l, то r1 r2 ≈ r2 и r1 − r2 ≈ l cosα. Если дополнительно воспользоваться определением модуля

где r = x2 + y2 + z2 .

ности поля описываются уравнением: cosr2α = const. Подставим формулу (**) в (1.28), получим:

1.11. Градиент как потенциальный вектор

Приведем небольшое обобщение результатов предыдущих параграфов. Поле вектора напряженности E(x, y, z) является градиентом скалярного поля ϕ(x, y, z): E = − ϕ. Говорят: вектор E электростатического поля яв-

ляется потенциальным вектором, а скалярная функция ϕ − потенциалом этого векторного поля.

Примерами потенциальных векторов являются центральные силы вида F(r). К этим силам относятся, например, гравитационная сила (и сила тяжести), кулоновская сила, сила упругости. Центральные силы зависят только от расстояния между взаимодействующими телами.

Работа центральной силы по замкнутому контуру в стационарном (!) потенциальном поле равна нулю. Стационарность потенциального поля в выбранной системе отсчета выражается в том, что потенциал ϕ и потен-

циальная энергия W такого поля явно от времени не зависит, т.е. ∂∂ϕt = 0

и ∂∂Wt = 0. Напомним, стационарные потенциальные силовые поля назы-

ваются консервативными полями, и признаком таких полей является усло-

ном силовом поле нет физически выделенных моментов времени, время в таком поле однородно. Напомним, это обусловливает связь закона сохранения механической энергии в консервативной системе с однородностью времени.

Напомним, дивергенция и градиент инвариантны относительно выбора системы координат.

Таким образом, определение поля E(x, y, z) по заданному распреде-

лению зарядов ρ(x, y, z) сводится к определению потенциала поля ϕ(x, y, z) по уравнению Пуассона, и, далее, определяется напряженность поля E (x, y, z) как градиент потенциала.

Для точек поля, где отсутствуют заряды (плотность заряда ρ(x, y, z) = 0),

Уже по структуре дифференциальных уравнений Пуассона и Лапласа можно судить о некоторых общих соответствующих свойствах

потенциала ϕ(x, y, z). Проведем, например, анализ (1.31) и (1.32) на экс-

тремум функции ϕ(x, y, z). Воспользуемся признаком обнаружения экстремума функции, основанный на определении знака второй производной ( одно из правил Лопиталя): в точках, где вторая производная от функции отрицательна, там функция имеет максимум, где положи-

тельна − минимум.

В уравнении (1.31) сумма вторых производных в данной точке пространства определяется плотностью заряда в этой точке, взятой с обратным знаком. Следовательно, в тех точках пространства, где содержатся положительные заряды (в этом случае сумма вторых производных имеет

отрицательный знак), там потенциал ϕ(x, y, z) принимает максимальное

значение; в точках с отрицательными зарядами потенциал ϕ(x, y, z) принимает минимальное значение, т.к. сумма производных положительна. В (1.32) сумма вторых производных равна нулю, поэтому потенциал

ϕ(x, y, z) в пространстве, где отсутствую заряды, изменяется монотонно (экстремум отсутствует).

Уравнение Лапласа позволяет провести расчет электрических полей в области пространства, где отсутствуют заряды, при известных граничных условиях этого пространства. Этими граничными условиями могут быть, например, распределения зарядов на границе пространства, потенциала на границе и др. В качестве иллюстрации сказанному, рассмотрим примеры расчета поля с помощью уравнения Лапласа.

Подставив граничные условия в решение (**), получим:

C2 = 0, C1h = ϕ0.

Итак, решение (**) с учетом граничных условий запишется в виде:

Определим напряженность поля: E = − ϕ = − ∂∂ϕx i, поэтому

Из формулы (***) следует, что потенциал изменяется по линейному закону от x. Из формулы (****) следует, что поле в конденсаторе однородно, т.е. напряженность одинакова во всех точках области существования поля (не считая краевых эффектов) и направлена в сторону убыли потенциала (здесь направлена против оси 0X, и отсюда знак минус).

Определим поверхностную плотность заряда на пластинах конденсатора. У поверхности пластин E = εεσ0 (§1.2). Для левой пластины имеем:

Для правой пластины:

Заряд пластин q = σ S = εε 0hϕ0S ; емкость конденсатора С =ϕ0q− 0 = εεh0S .

Задача о вычислении поля заряженной сферы. Проводящая сфера радиуса a

заряжена до потенциала ϕ0. Рассчитать поле этой сферы.