введение в тфп

между этими волнами. Сравнение уравнений (11) и (16) показывает, что

то волны «1» и «3» находятся в фазе, и их амплитуды складываются – наблюдается максимум интерференции этих волн. В противном случае волны будут гасить друг друга. Подставляя связь между круговой частотой

и длиной волны ω = 2λπc в соотношение (17), получим:

Синфазное распространение волн «1» и «3» реализуется, если на длине струны укладывается целое число полуволн.

Аналогичный результат получится и для волн, бегущих справа налево − опоры B к опоре A. При этом волны, бегущие от B к A, находятся

в противофазе с волнами, бегущими от A к B за счет сдвига фазы на π радиан при отражении от опоры.

Итак, при выполнении условия (17) (или 18), волны, бегущие в од-

ном направлении, движутся в фазе и их амплитуды складываются.

Подчеркнем еще раз: если условие (17) (или 18) не выполняются, то при многократном отражении разность их фаз непрерывно изменяется, что приводит к уменьшению результирующей амплитуды, волны начинают гасить друг друга.

В реальном эксперименте потери энергии при отражении неизбежны, неизбежно также и затухание волны при распространении по струне. Часть

энергии волны передается устройствам крепления струны − опорам, а часть переходит во внутреннюю энергию материала струны, в результате чего струна нагревается. Поэтому полученное равенство амплитуд бегущих волн a 1 = a2 = … = am = ... не выполняется – амплитуды am уменьша-

ются. Вследствие потерь энергии сдвиг фазы на π радиан при отражении также точно не выполняется, ибо в точках крепления струны наблюдаются незначительные колебания, обеспечивающие передачу энергии креплению струны.

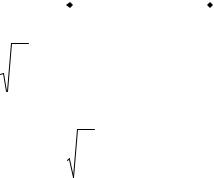
Уравнение стоячей волны. Результирующее колебание струны обусловлено интерференцией встречных волн. Обозначим результирующую амплитуду волн (при выполнении условия (17)), бегущих в положительном

направлении оси 0x, через Y(→) , а в обратном направлении – через Y(←). Здесь: Y(→) = a1 + a3 + a5 + … ; Y(←)= a2 + a4 + a6 + … (на рис. 3 стрелками

152

152 Приложение 1

показаны только волны y1, y2, y3). Вследствие потерь энергии результи-

рующие амплитуды Y(→) и Y(←) имеют конечное значение (не бесконечно большое!) и не равны друг другу. Уравнение результирующей волны, бегущей в положительном направлении оси 0x, имеет вид:

y(→) = Y(→) sin (ωt – kx).

Уравнение результирующей волны, бегущей в отрицательном направлении оси 0x, имеет вид:

y(←) = Y(←) sin (ωt + kx + π) = − Y(←) sin (ωt + kx).

Результирующая волна y на струне определится суммой встречных бегу-

щих волн:

y = y(→) + y(←) = Y(→) sin (ωt – kx) − Y(←) sin (ωt + kx).

Прибавим и вычтем вспомогательную величину [Y(→) sin (ωt + kx)], получим:

y = [Y(→) sin (ωt – kx) – Y(→) sin (ωt + kx)] + [Y(→) sin (ωt + kx) − Y(←) sin (ωt + kx)],

Уравнение (19) описывает волновой процесс в струне.

Проведем анализ уравнения.

1. При Y(→) = Y(←) в уравнении (19) остается первый член, который описывает стоячую волну: y = −2Y(→) sin kx cos ωt . Второй член в (19) равен

нулю. Амплитуда колебаний частиц струны (2Y(→)sinkx) определяется координатой этих частиц. В точках с координатами, отвечающими условию sin

kx = 0, т .е. условию kx = nπ, колебания отсутствуют. Эти точки на струне называются узлами стоячей волны. Координаты узлов: т.к. k = 2λπ , то

В частности, в точках крепления (x = 0 и х =L) находятся узлы стоячей волны. Имеем L = n λ2 , т.е. при реализации на струне стоячей волны, на

струне укладывается целое число полуволн. Полученное соотношение (20) коррелируется с формулой (18). При заданной длине струны L определим

набор собственных частот струны νn , при которых формируется стоячая волна: так как L = n λ2 = n 2νcn , то:

Фазовая скорость может быть рассчитана из экспериментальных данных

при данном натяжении T дисперсия отсутствует.

Частота ν1 (n = 1, т.е. на струне укладывается одна полуволна), называется основным тоном струны, остальные собственные частоты называ-

ются обертонами. Собственные частоты − основной тон и обертона − еще называют резонансными частотами.

Обратим внимание на то обстоятельство, что собственные частоты (22) при малых колебаниях не зависят от собственных упругих свойств материала струны. Частота определяется внешним натяжением (задаваемым в эксперименте грузом) и плотностью струны, но не зависит от модуля Юнга, характеризующего собственные упругие свойства материала струны. Другими словами, если взять две струны из разных материалов,

но c одинаковой линейной плотностью ρ, и приложить к ним одинаковую силу натяжения T, то набор собственных частот этих двух струн будет одинаковым. Этот вывод обусловлен тем, что мы пренебрегли растяжением струны и считали, что сила натяжения одинакова во всех элементах струны при возбуждении колебаний. Разумеется, для струн из различных материалов растяжение при данной нагрузке T различно и определяется модулем Юнга.

В точках струны, отвечающих условию sin kx = 1 ( т.е. при условии kx =(2n + 1) π2 , где n = 1, 2, …) имеем максимумы амплитуды ко-

лебания в стоячей волне. Эти максимумы называются пучностями стоя-

чей волны. Итак, из условия sin kx = 1 получаем выражение для координат пучностей:

В пучностях амплитуда стоячей волны имеет максимальное значение

и равна 2 Y(→), а по мере приближения к узлам, амплитуда колебаний уменьшается

График стоячей волны в отсутствии потерь приведен на рис. 4. Частицы струны между узлами колеблются в фазе. При переходе через

узел фаза изменяется на π радиан ( противофазные колебания частиц на соседних участках струны при переходе через узел).

Пучности

y

2Y(→)

x

0

x=L

λ/2 Узлы

Рис. 4

2. В стоячей волне энергия не переносится, в узлах колебания отсутствуют. Однако в отсутствии потерь нет и необходимости компенсировать по-

тери. В реальном же эксперименте потери неизбежны, поэтому Y(→) ≠ Y(←). Энергия от источника переносится бегущей волной описываемой вторым слагаемым в (19), тем самым компенсируются потери энергии волны при отражении и потери за счет затухания волны в струне.

В реальном эксперименте бегущая волна вызывает небольшие колебания в узлах, вследствие чего узлы размываются. Величину амплитуды

бегущей волны Aбег. = (Y(→) − Y(←)) можно оценить по размаху колебания узлов.

В линейном приближении, т.е. при малых колебаниях струны, максимальная амплитуда стоячей волны 2Y(→) много больше амплитуды бегущей волны Aбег.: 2Y(→) >> Aбег.

Приложение 2. Формулы и теоремы векторного исчисления

Векторные величины в тексте обозначены прямым полужирным шрифтом, скалярные – курсивом. Например, b – вектор, b – скаляр. точкой между сомножителями. Скалярное произведение векторов векторов a и b записывается как (ab). Векторное произведение обозначено заключением сомножителей в квадратные скобки через запятую. Например, векторное произведение векторов a и b записывается как [a, b].

1.Векторная алгебра

1.1. Скалярное произведение векторов ab называется произведение модулей векторов на косинус угла между этими векторами:

ab = ab cos(a^b).

Выражение скалярного произведения через компоненты векторов в декартовой системе координат:

ab = (ax i + ay j + az k) (bx i + by j + bz k) = ax bx + ay by + az bz ,

где i, j, k – единичные орты, ii = jj = kk = 1, ij = jk = ki = 0.

1.2. Векторное произведение двух векторов [a, b]. В результате векторного произведения векторов a и b получается новый вектор c: [a, b] = c. Модуль результата векторного произведения – модуль вектора с - по определению равен c = ab sin (a^b). В декартовой системе координат векторное произведение имеет вид

[a, b] = [(ax i +ay j +az k) (bx i +by j +bz k)] = (ay bz − az by)i + (az bx − ax bz)j + (ax by − ay bx)k.

Векторное произведение [a, b] можно представить в форме определителя:

1.3. Смешанное (скалярно-векторное) произведение трех векторов а[bc]. Результатом такого произведения является скалярная величина:

а[b, c] = axbycz − axbzcy + aybzcx − aybxcz + azbxcy − azbycx .

Смешанное произведение допускает циклическую (стековую) перестановку векторов:

а[b, c] =c[а, b] = b[c, а].

По своему геометрическому смыслу смешанное произведение равно объему параллелепипеда, построенного на векторах а, b и c.

1.4.Двойное векторное произведение [а, [bc]]:

[а, [b, c]] = b(ac) − c(ab).

Здесь вначале выполняются скалярные произведения, стоящие в скобах (т.е. скалярные произведения ac и ab), и только затем вектора b и c

умножаются на соответствующие результаты скалярного произведения. Компоненты результата двойного векторного произведения имеют вид:

[а, [bc]]x = bx (ac) − cx (ab), [а, [bc]]y = by (ac) − cy (ab), [а, [bc]]z = bz (ac) − cz (ab).

При проведении циклической перестановки в двойном векторном произведении получаются три разных вектора, сумма которых равна нулю:

[а,[b, c]] +[c,[а, b]] +[b, [c, а]] = 0

2.Векторный анализ

2.1.Векторный оператор набла (оператор Гамильтона) как символический вектор:

= ∂∂x i + ∂∂y j + ∂∂z k.

2.2.Градиент скалярной функции (скалярного поля) ϕ(x, y, z) – это век-

тор, направленный в сторону быстрейшего увеличения ϕ и равный производной по этому направлению. В координатном представлении градиент имеет вид:

gradϕ = ϕ (в развернутом виде ϕ = ∂∂ϕx i + ∂∂ϕy j + ∂∂ϕz k).

2.3. Дивергенция некоторого вектора E в данной точке пространства – это поток вектора E из бесконечно малого объема dV, находящегося в этой точке пространства. Объем dV – источник или сток вектора E. Дивергенция вектора E – скалярная величина и определяется скалярным произведением оператора набла на вектор E:

div E ≡ E. В развернутом виде E = ∂∂Exx + ∂∂Eyy + ∂∂Ezz .

2.4. Ротор некоторого вектора E – это вектор, порождающий циркуляцию некоторого другого вектора по бесконечно малому контуру. Напри-

мер, в уравнении Максвелла rot Е = − ∂∂Bt вектор ∂∂Bt является ротором, ко-

торый порождает вихревой вектор – напряженность вихревого электрического поля Е. Ротор вектора E – векторная величина и определяется

векторным произведением оператора набла на вектор E: rotE ≡ [, E].

2.5.Некоторые векторные тождества.

1. (ϕ) = 2ϕ = ∂2ϕ + ∂2ϕ + ∂2ϕ , где ϕ - скалярная функция.

∂x2 ∂y2 ∂z2

2.[ , (ϕ)] = 0.

3.[ , E] = 0, где E - векторная функция.

4.[ , [ , E]] = ( E) −2E.

5.(δϕ) = δ ϕ + ϕ δ, где δ и ϕ - скалярные функции.

6.(ϕ E) = ϕ ( E) + Eϕ.

7.[ (ϕ E)] = ϕ [ E] + [(ϕ) E].

2.6.Теоремы векторного анализа.

1.Теорема Гаусса. Здесь объем V ограничен замкнутой поверхностью S. Вектор dS в данной точке замкнутой поверхности направлен по внешней нормали к поверхности.

2. Теорема Стокса. Здесь замкнутый контур L ограничивает поверхность S, натянутая на контур. Вектор dl (как элемент контура L) по направлению совпадает с положительным обходом контура. Положительный обход контура связан с положительной нормалью к поверхности S правилом правого винта.

СОДЕРЖАНИЕ

3. Электромагнитная индукция 41

3.1. Закон электромагнитной индукции Фарадея.

Физическая природа электромагнитной индукции 41

3.2. Самоиндукция. Индуктивность проводника 43 3.3. Магнитная энергия 44

4. Электродинамика 46

4.5.1.Из уравнений Максвелла вытекает существование электромагнитного излучения (электромагнитной

волны) 64

4.5.2.Волновое уравнение плоской электромагнитной волны в идеальном диэлектрике в отсутствии потерь.

Решение волнового уравнения, свойства волны 67

4.9.6.Оценка распределение плотности потока переносимой электромагнитной энергии в пространстве

4.10.1.Отражение и преломление плоской электромагнитной волны при нормальном падении на границу

раздела сред 109

4.10.2.Отражение и преломление плоской электромагнитной волны при наклонном падении на границу

раздела сред 113

4.10.3.Распространение плоской электромагнитной волны в проводящей (поглощающей) среде при наклонном

4.11.2.Распространение электромагнитной волны между параллельными идеально

проводящими поверхностями 129

4.11.3. Прямоугольный металлический волновод 139

Приложение 2. Формулы и теоремы векторного исчисления 155