
- •Самарина е.Ф.
- •Оглавление
- •§3. Прямоугольная декартова система координат . . . . . . . . . . . . . . . . . . . . . . . . . .30
- •§4. Скалярное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32
- •§5. Векторное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34
- •§6. Смешанное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .37
- •Предисловие в учебное пособие вошли все разделы стандартного курса математики содержащихся в первом семестре.
- •§1. Определители и матрицы
- •§2. Линейное (векторное) пространство.
- •§3. Cистемы линейных алгебраических уравнений.
- •§2.Линейные операции над векторами.
- •§2 Линейная комбинация векторов
- •§3. Прямоугольная декартова система координат
- •§4.Скалярное произведение векторов.
- •§5. Векторное произведение векторов.
- •§6.Смешанное произведение векторов
- •Решение системы находим по формулам Крамера
- •Вариант 1
- •Вариант 11
- •Вопрос 1. Что такое матрица?
§6.Смешанное произведение векторов
Определение
1. Смешанное
произведение векторов
 называется число, равное скалярному
произведению вектора
называется число, равное скалярному
произведению вектора
 на
вектор
на
вектор т.е. [
т.е. [
Свойства смешанного произведения
[

В
силу этого свойства смешанного
произведения векторов
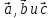 обозначают просто
обозначают просто
Циклическое свойство [

Если векторы
 в ортогональном базисе заданы своими
координатами
в ортогональном базисе заданы своими
координатами то смешанное произведение вычисляется
по формуле
то смешанное произведение вычисляется
по формуле

Геометрический смысл смешанного произведения
Абсолютная величина смешанного произведения векторов
 численно равнаобъёму
численно равнаобъёму
 параллелепипеда,построенного
на этих векторах, т.е.
параллелепипеда,построенного
на этих векторах, т.е.
 Кроме того, │
Кроме того, │ объём треугольной пирамиды, построенной
на векторах
объём треугольной пирамиды, построенной
на векторах ,
,
Условие компланарности трёх векторов. Необходимым и достаточным условием компланарности векторов
 является равенство нулю их смешанного
произведения, т.е.
является равенство нулю их смешанного
произведения, т.е.
В координатной форме условие компланарности имеет вид:

Пример
1. Найти
смешанное произведение векторов
 заданных своими координатами:
заданных своими координатами:
Решение.
Геометрическое значение этого результата: данные векторы компланарны (п.2, п.3, п.4 – самостоятельно). (При вычислении определителя мы пользовались разложением его по элементам третьего столбца).
Ответ: 14.
Задания для самостоятельного решения
Установить, компланарны ли векторы

а)

б)

в)
 .
.
2.
Даны вершины тетраэдра:
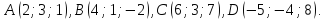 Найти длину его высоты, опущенной из
вершины
Найти длину его высоты, опущенной из
вершины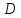 .
.
3.Объём
тетраэдра равен
 три его вершины находятся в точках
три его вершины находятся в точках Найти координаты четвёртой вершины
Найти координаты четвёртой вершины если известно, что она лежит на ости
если известно, что она лежит на ости
4.
Доказать, что четыре точки
 лежат в одной плоскости.
лежат в одной плоскости.
5.
Векторы
 правую
тройку, взаимно перпендикулярны и │
правую
тройку, взаимно перпендикулярны и │ Вычислить
Вычислить .
.
6.
Заданы векторы
 Вычислить
Вычислить Какова ориентация троек: а)
Какова ориентация троек: а)
7.
Вычислить объём тетраэдра с вершинами
в точках

8.
Доказать тождество

Типовые решения примеров и задач
Элементы линейной алгебры
Пример : Вычитание матриц выполнимо только тогда, когда матрицы одинакового размера
Дана матрица размером 4х2;

Элементы первой матрицы вычитаем из соответствующих элементов второй матрицы;
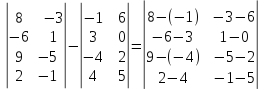 =
=
Пример : Сложение матриц выполнимо только тогда, когда матрицы одинакового размера
Дана матрица размером 4х2;
 Складываем
элементы первой матрицы с соответствующими
элементами второй матрицы;
Складываем
элементы первой матрицы с соответствующими
элементами второй матрицы;
 =
=
Пример : Пример умножения матрицы на число (константу)
Дана матрица размером 4х3 и число 4;
 Нужно
умножить каждый элемент матрицы на 4
Нужно
умножить каждый элемент матрицы на 4

Пример
: Вычислить определитель второго
порядка
Главная диагональ
Побочная диагональ
Дана
матрица размером 2х2; 


Что бы вычислить определитель матрицы 2х2 нужно из произведения элементов главной диагонали, вычесть произведение элементов побочной диагонали;

Ответ: -6
Пример : Вычислить определитель третьего порядка
Дана матрица размером 3х3;

Что бы вычислить определитель матрицы 3х3 нужно воспользоваться формулой;
 =
=








Подставляем наши значения в формулу;


Ответ: -642
Пример : Вычислить определитель четвертого порядка
Дана матрица размером 4х4;

Есть два способа вычисления определителя матрицы:
По определению - через разложение по строке или столбцу;
По методу Гаусса - приведение матрицы к треугольному виду (этот способ лучше использовать для решения матриц, размером 4х4 и более).
Решим пример первым способом (по определению - через разложение по строке или столбцу)
Чтобы вычислить определитель матрицы, нужно воспользоваться следующей формулой, в ней рассмотрен пример разложения матрицы по первой строке;

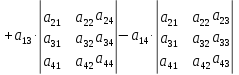
Итак, начнём
Выбираем строку или столбец (любую), лучше всего выбирать строку или столбец, где больше нулей, для удобства вычисления;
В данном случае мы выбираем третью строку, так как в ней присутствует ноль;

Берём первый элемент этой строки (2);
Теперь
вычёркиваем третью строку и первый
столбец;

Получаем матрицу 3х3;

Согласно формуле, мы умножаем выбранный нами элемент на определитель получившейся матрицы;
Вычисление определителя матрицы 3х3, мы рассматривали в примере №2



Далее делаем всё тоже самое, что и в шаге два, только берём второй элемент данной строки (0) и вычёркиваем третью строку и второй столбец;


Так как этот элемент равен нулю, то ни чего не нужно считать и так всё ясно;
Теперь берём третий элемент строки (6) и вычёркиваем третью строку и третий столбец;

Получаем матрицу 3х3;

Вычисляем определитель этой матрицы и умножаем на выбранный нами элемент (6)
 =
=

Берём четвёртый элемент строки (-3) и вычёркиваем третью строку и четвёртый столбец;

Получаем матрицу 3х3;

Вычисляем определитель этой матрицы и умножаем на выбранный нами элемент (-3)



Чтобы вычислить определитель исходной матрицы, нужно сложить полученные результаты;
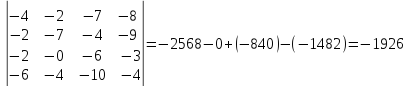
Ответ: -1926
Опишем решение примера вторым способом (по методу Гаусса - приведение матрицы к треугольному виду)
Суть способа заключается в том, чтобы перед вычислением определителя, привести матрицу к треугольному виду. Если в ходе приведения матрицы к треугольному виду вы умножаете (делите) строку на число, то на это же число нужно будет умножить (разделить) полученный в конце определитель;
Пример приведения матрицы к треугольному виду мы уже рассматривали
Итак, мы привили матрицу к треугольному виду;

Теперь чтобы вычислить определитель приведённой матрицы, нужно перемножить все элементы, стоящие на главной диагонали;

Ответ: -1926
Пример:
Перемножить матрицы:
![]() -
размером (2 х 3)
-
размером (2 х 3)
 -
размером (3 x 3)
-
размером (3 x 3)
Решение:
Так как число столбцов А(3)совпадает с числом строкВ (3), следовательно, можно их перемножить.
Чтобы получить элемент С11произведения, умножим первую строку матрицыАна первый столбец матрицыВ.
С11= 1·1 + 2·0 + 3·2 = 7,
С12 получится умножением первой строкиА на второй столбецВ:
С12= 1·2 + 2·2 +3·2 = 12
С13– умножением первой строкиАна третий столбецВ:
С13= 1·3 + 2·0 + 3·1 = 6
С21–умножением второй строкиА на первый столбецВ:
С21= 0·1 = 1·0 +2·2 = 4
Далее, умножая вторую строку Ана второй столбецВ, получимС22=6, умножая вторую строкуАна третий столбецВ, получимС23=2
Больше у нас строк нет. Получилась матрица С, состоящая из двух строк и трех столбцов
Пример:
Найдем обратную матрицу к матрице A

Как видно из формулы А-1, нам придется делить на определитель А, поэтому важно, а не окажется ли он равен нулю? Разложим А по первой строке, это нам удобно, т.к. там много нулей.
![]()
Определитель нулю не равен, значит обратная матрица существует.
Найдем
алгебраические дополнения (знаки их
учтем сразу) то есть

Векторная алгебра
Пример
.Построить вектор
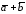 .
.
Решение:
Пример
. Найти длину вектора;Даны
точки:
Решение:


Пример
Найти
угол между векторами
 где
где
Решение:
Косинус угла между векторами вычисляется по формуле:

Пример
Пусть
 =
= .
Найти направляющие косинусы данного
вектора, а также углы
.
Найти направляющие косинусы данного
вектора, а также углы и
и .
.
Решение.
 =
=
 ,
, =
= ,
, =
= =
= = 3;
= 3;

 =
=
 =
= ,
,
 =
= =
= .
Отсюда
.
Отсюда =
= ,
, =
= .
.
Пример
Найти
векторное произведение
 ;
Даны точки:
;
Даны точки:
Решение:

Векторное
произведение векторов вычисляется по
формуле:
 где
где
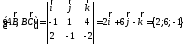 ;
;
Пример
Найти
скалярное произведение векторов;Даны
точки:

Решение:

Вычисляем скалярное произведение векторов:

Пример
Найти
смешанное произведение
 ;
Даны точки:
;
Даны точки:
Решение:
Смешанное
произведение векторов вычисляется по
формуле: ,
где
,
где

Пример
Коллинеарны
ли векторы
 и
и ,
разложенные по векторам
,
разложенные по векторам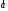 и
и ,
где
,
где
Решение:
1.
Вычислим проекции векторов
 :
:


2. Два вектора коллинеарны, если их проекции пропорциональны, следовательно, проверим пропорциональность проекций векторов:
 не
коллинеарны
не
коллинеарны
Пример
Найти
решение системы линейных алгебраических
уравнений Методом Крамера:
 .
.
Решение:
Решение системы находим по формулам Крамера:
 .
.
Вычислим
определитель системы

 .
.
Последовательно
заменив в
 ,
первый, второй и третий столбцы столбцом
свободных членов, получим соответственно
,
первый, второй и третий столбцы столбцом
свободных членов, получим соответственно
 ;
;
 ;
;
 .
.
Ответ:
 .
.
Пример
Найти решение системы линейных алгебраических уравнений методом Гаусса (или методом исключения неизвестных):
 .
.
Решение:
Выпишем
расширенную матрицу
 данной системы и приведем ее к ступенчатому
виду
данной системы и приведем ее к ступенчатому
виду
 .
.
Последовательно умножим первую строку на (–2) и прибавим ее ко второй строке, затем умножим на (–3) и прибавим к третьей строке, умножим на (–2) и прибавим к четвертой строке, получим
 .
.
Ко
второй строке полученной матрицы
прибавим третью строку, умноженную на
 ,
затем во вновь полученной матрице
умножим третью строку на
,
затем во вновь полученной матрице
умножим третью строку на ,
четвертую – на (–1), затем последовательно
умножим вторую строку на 2 и прибавим
ее к третьей строке, умножим на 7 и
прибавим к четвертой строке, получим
,
четвертую – на (–1), затем последовательно
умножим вторую строку на 2 и прибавим
ее к третьей строке, умножим на 7 и
прибавим к четвертой строке, получим
 .
.
Третью
строку полученной матрицы умножим на
 ,
четвертую – на
,
четвертую – на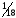 ,
затем третью строку умножим на (–1) и
прибавим к четвертой строке, получим
,
затем третью строку умножим на (–1) и
прибавим к четвертой строке, получим
 .
.
Найденная матрица имеет треугольный вид; по этой матрице запишем систему уравнений, эквивалентную исходной системе,
 .
.
Последовательно
находим неизвестные, начиная с последнего
уравнения,
 ;
подставим в третье уравнение найденное
;
подставим в третье уравнение найденное ,
вычислим
,
вычислим ,
, ;
затем из второго уравнения находим
;
затем из второго уравнения находим ,
, ;
из первого уравнения получим
;
из первого уравнения получим ,
, .
.
Ответ:
 .
.
Пример
Найти общее решение однородной системы линейных алгебраических уравнений (Использованиетеоремы Кронекера-Капелли):
 .
.
Решение.
Элементарными
преобразованиями строк приведем матрицу
системы
 к эквивалентной матрице
к эквивалентной матрице ,
которой соответствует уравнение
,
которой соответствует уравнение , эквивалентное исходной системе. Таким
образом, общее решение может быть
записано в форме
, эквивалентное исходной системе. Таким
образом, общее решение может быть
записано в форме , или
, или ,
, . Решений бесчисленное множество –
любая пара, связанная указанной
зависимостью, обращает левые части
уравнений данной системы в нуль. В
системе
. Решений бесчисленное множество –
любая пара, связанная указанной
зависимостью, обращает левые части
уравнений данной системы в нуль. В
системе - число неизвестных и число уравнений.
- число неизвестных и число уравнений. ,
, матрица
системы,
матрица
системы, расширенная
матрица системы. В силу теоремы
Кронекера-Капелли система имеет
бесчисленное множество решений, зависящих
от одного параметра
расширенная
матрица системы. В силу теоремы
Кронекера-Капелли система имеет
бесчисленное множество решений, зависящих
от одного параметра .
Иногда общее решение удобнее использовать
в форме
.
Иногда общее решение удобнее использовать
в форме
Ответ:
 .
.
5.
При каких значениях
 система
система

имеет нетривиальные (ненулевые) решения ? Найти эти решения.
Решение.
Однородная
система линейных уравнений имеет
ненулевые решения, когда ее определитель
равен нулю. Из этого условия и найдем
соответствующие значения
 :
:
 .
.
Найдем теперь соответствующие решения.
1)
При
 система имеет вид :
система имеет вид :
 .
.
Определитель этой системы равен нулю. Это означает наличие линейной зависимости между уравнениями системы. Замечаем, что первое уравнение получается из второго и поэтому его можно отбросить. Имеем
 .
.
Так
как определитель из коэффициентов при
неизвестных
 не равен нулю, то в качестве базисных
неизвестных возьмем
не равен нулю, то в качестве базисных
неизвестных возьмем (хотя можно брать и другие пары неизвестных)
и перенесем члены с
(хотя можно брать и другие пары неизвестных)
и перенесем члены с в правые части уравнений :
в правые части уравнений :
 .
.
Полученную систему можно решить по формулам Крамера :
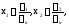
где
 ,
, ,
, .
.
Тогда
 ,
, . Полагая
. Полагая , где
, где произвольное действительное число ,
получаем решение системы :
произвольное действительное число ,
получаем решение системы : ,
, ,
, .
.
2)
При
 система имеет вид :
система имеет вид :
 .
.
Можно
решить эту систему и методом Гаусса.
Составим расширенную матрицу
 полученной системы :
полученной системы :
 и
приведем ее к матрице ступенчатого
вида :
и
приведем ее к матрице ступенчатого
вида :


 .
.
Восстановим систему для полученной матрицы






 .
.
Полагая
 , где
, где произвольное
действительное число, получаем решение
системы :
произвольное
действительное число, получаем решение
системы : .
.
Ответ
: При
 система имеет нетривиальные решения :
система имеет нетривиальные решения : ,
, ,
, ,
, . При
. При система имеет нетривиальные решения :
система имеет нетривиальные решения : ,
, .
.
Модуль 6.
Задания для текущей аттестации/зачета по теме: Линейная алгебра
Решение типового варианта по теме линейная алгебра
1. Методом Крамера найти решение системы линейных алгебраических уравнений
 .
.
Решение.




