
- •Самарина е.Ф.
- •Оглавление
- •§3. Прямоугольная декартова система координат . . . . . . . . . . . . . . . . . . . . . . . . . .30
- •§4. Скалярное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32
- •§5. Векторное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34
- •§6. Смешанное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .37
- •Предисловие в учебное пособие вошли все разделы стандартного курса математики содержащихся в первом семестре.
- •§1. Определители и матрицы
- •§2. Линейное (векторное) пространство.
- •§3. Cистемы линейных алгебраических уравнений.
- •§2.Линейные операции над векторами.
- •§2 Линейная комбинация векторов
- •§3. Прямоугольная декартова система координат
- •§4.Скалярное произведение векторов.
- •§5. Векторное произведение векторов.
- •§6.Смешанное произведение векторов
- •Решение системы находим по формулам Крамера
- •Вариант 1
- •Вариант 11
- •Вопрос 1. Что такое матрица?
§2.Линейные операции над векторами.
Понятие вектора
Определение 1. Вектором называется направленный отрезок ( или, что то же, упорядоченная пара точек).
Обозначают:
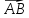 (точка А-начало вектора), точка В – конец
вектора) или одной буквой -
(точка А-начало вектора), точка В – конец
вектора) или одной буквой -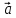 .
.
Определение
2. Длиной вектора (модулем)называется
расстояние между началом и концом
вектора. Длина вектора обозначается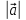 или
или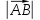 .
.
Определение
3. Нулевым вектором называется
вектор, у которого начало и конец
совпадают. Обозначают: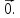
Определение 4. Единичным векторомназывается вектор, длина которого равна единице.
Единичный
вектор, имеющий одинаковое направление
с данным вектором
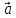 ,
называется ортом вектора
,
называется ортом вектора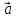 и обозначается символом
и обозначается символом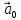 .
.
Определение 5. Векторы называютсяколлинеарными, если они расположены на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому вектору.
Определение 6. Векторы называютсяравными, если они коллинеарны, имеют одинаковые длины и одинаковое направление.
Линейные операции над векторами
Определение 7. Линейными операциями над вектораминазываются сложение векторов и умножение вектора на число.
Определение
8. Суммой
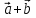 двух векторов
двух векторов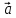 и
и называется
вектор
называется
вектор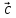 ,
который идет из начала вектора
,
который идет из начала вектора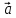 в конец вектора
в конец вектора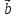 при условии, что вектор
при условии, что вектор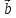 приложен к концу вектора
приложен к концу вектора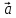 (правило треугольника). В случае
неколлинеарных векторов
(правило треугольника). В случае
неколлинеарных векторов и
и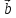 можно
вместо правила треугольника использовать
правило параллелограмма: если векторы
можно
вместо правила треугольника использовать
правило параллелограмма: если векторы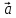 и
и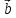 отложены от общего начала и на них
построен параллелограмм, то сумма
отложены от общего начала и на них
построен параллелограмм, то сумма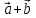 есть вектор, совпадающий с диагональю
этого параллелограмма, идущего из общего
начала
есть вектор, совпадающий с диагональю
этого параллелограмма, идущего из общего
начала и
и .
.
Определение
9. Разностью
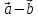 двух
векторов
двух
векторов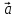 и
и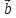 называется вектор
называется вектор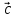 ,
который в сумме с вектором
,
который в сумме с вектором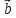 составляет вектор
составляет вектор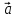 .
Если два вектора
.
Если два вектора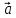 и
и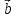 отложены от общего начала, то их разность
есть вектор, исходящий из конца вектора
отложены от общего начала, то их разность
есть вектор, исходящий из конца вектора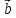 («вычитаемого») к концу вектора
(«вычитаемого») к концу вектора («уменьшаемого»).
(«уменьшаемого»).
Определение
10. Два коллинеарных вектора равной
длины, направленные в противоположные
стороны, называются противоположными.
Вектор, противоположный вектору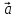 , обозначается
, обозначается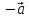 .
.
Произведение
вектора
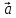 на число
на число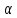 обозначают α
обозначают α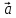 .
.
Некоторые свойства линейных операций
1)
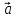 +(
+(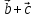 )=(
)=(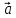 +
+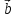 )+
)+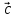 ;
;
2)
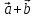 =
=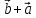 ;
;
3)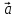 +
+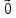 =
= ;
;
4)
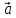 +(
+(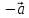 )=
)=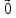 ;
;
5)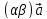 =
= (
(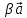 );
);
6)
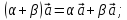
7)
 ;
;
8)
1·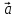 =
=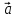 .
.
Теорема
1. (О коллинеарных векторах). Если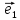 и
и – два коллинеарных вектора, причем
вектор
– два коллинеарных вектора, причем
вектор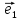 -ненулевой,
то существует единственное число х
такое, что
-ненулевой,
то существует единственное число х
такое, что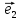 =х
=х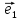
В
частности, ненулевой вектор
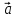 и его орт
и его орт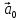 связаны равенством:
связаны равенством: =
=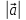 ·
·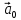 .
.
Сформулированные свойства линейных операций позволяют преобразовать выражения, составленные из векторов, по обычным правилам алгебры: можно раскрыть скобки, приводить подобные члены, переносить некоторые члены в другую часть равенства с противоположным знаком и т.д.
Пример 1.
Доказать равенства:
а)
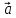 +
+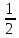 (
( )=
)= (
(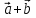 );
);
б)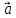 -
-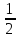 (
( )=
)=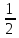 (
(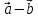 ).
).
и выяснить, каков их геометрический смысл.
Решение.
а) В левой части равенства раскроем
скобки, приведем подобные члены, получим
вектор в правой части. Поясним это
равенство геометрически. Пусть даны
два вектора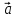 и
и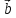 ,
отложим их от общего начала и посмотрим
параллелограмм и его диагонали, получим:
,
отложим их от общего начала и посмотрим
параллелограмм и его диагонали, получим:
§2 Линейная комбинация векторов
Векторный базис на плоскости и в пространстве.
Определение
1. Линейной комбинацией векторов
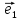 ,
,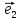 ,
,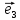 называется сумма произведений этих
векторов на какие-нибудь числа
называется сумма произведений этих
векторов на какие-нибудь числа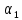 ,
,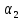 ,
, :
: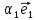 +
+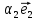 +
+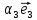 .
.
Определение
2. Векторным базисом в данной
плоскости называется любая пара
неколлинеарных векторов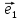 и
и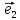 этой плоскости.
этой плоскости.
Вектор
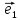 называют
при этом первым базисным вектором,
вектор
называют
при этом первым базисным вектором,
вектор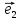 -вторым.
-вторым.
Справедлива следующая теорема.
Теорема
1.Если базис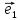 ,
,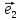 –векторный базис в плоскости, тогда
любой вектор
–векторный базис в плоскости, тогда
любой вектор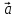 этой плоскости может быть представлен,
и притом единственным образом, в виде
линейной комбинации базисных векторов
этой плоскости может быть представлен,
и притом единственным образом, в виде
линейной комбинации базисных векторов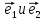 :
: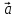 = х
= х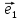 +у
+у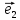 .
(*)
.
(*)
Определение
3. Равенство(*) называютразложением
вектора
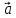 по базису
по базису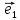 ,
,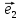 ,
а числа х и у –координатами вектора
,
а числа х и у –координатами вектора
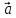 в базисе
в базисе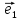 ,
,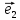 (
илиотносительно базиса
(
илиотносительно базиса
 ,
,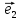 ).Если заранее ясно, о каком базисе идет
речь, то пишут кратко:
).Если заранее ясно, о каком базисе идет
речь, то пишут кратко: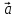 ={x,y}. Из
определения координат вектора относительно
базиса следует, что равные векторы имеют
соответственно равные координаты.
={x,y}. Из
определения координат вектора относительно
базиса следует, что равные векторы имеют
соответственно равные координаты.
Два и более векторов в пространстве называются компланарными, если они параллельны одной и той же плоскости или лежат в этой плоскости.
Определение
4. Векторным базисом в пространстве
называют любые три вектора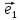 ,
, ,
,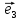 .
.
Вектор
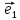 называют при этом первым базисным
вектором,
называют при этом первым базисным
вектором,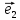 - вторым,
- вторым,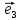 -третьим.
-третьим.
Замечание.
1. Три вектора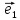 =
{
=
{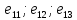 },
},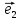 =
{
=
{ }
и
}
и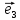 = {
= { }
образуют базис пространства, если
определитель, составленный из их
координат, отличен от нуля :
}
образуют базис пространства, если
определитель, составленный из их
координат, отличен от нуля :
 .
.
2. Основные положения теории определителей и способы их вычисления рассмотрены в модуле 1 «линейная алгебра».
Теорема
2. Пусть ,
, ,
,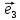 - векторный базис в пространстве. Тогда
любой вектор
- векторный базис в пространстве. Тогда
любой вектор в пространстве может быть представлен,
и притом единственным образом, в виде
линейной комбинации базисных векторов
в пространстве может быть представлен,
и притом единственным образом, в виде
линейной комбинации базисных векторов ,
,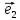 и
и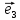 :
:
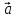 =
х
=
х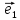 +у
+у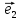 +z
+z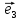 .
(**)
.
(**)
Определение
5. Равенство (**) называютразложением
вектора
 по базису
по базису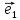 ,
,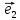 ,
, ,
а числаx,y,z–координатами
(компонентами) вектора
,
а числаx,y,z–координатами
(компонентами) вектора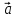 в базисе
в базисе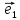 ,
,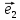 ,
,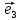 .
.
Если
заранее ясно, о каком базисе идет речь,
то пишут кратко:
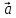 = {x,y,z}.
= {x,y,z}.
Определение
6. Базис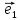 ,
,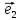 ,
,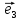 называетсяортонормированным, если
векторы
называетсяортонормированным, если
векторы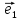 ,
,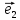 ,
,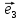 попарно перпендикулярны и имеют единичную
длину. В этом случае приняты обозначения
попарно перпендикулярны и имеют единичную
длину. В этом случае приняты обозначения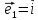 ,
,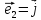 ,
,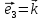 .
.
Действия над векторами, заданными своими координатами.
Теорема
3. Пусть на плоскости выбран векторный
базис ,
,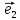 и относительно его векторы
и относительно его векторы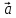 и
и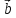 заданы
своими координатами:
заданы
своими координатами: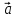 = {
= { },
},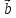 =
{
=
{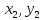 }.
}.
Тогда
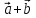 ={
={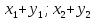 },
},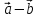 ={
={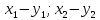 },
т.е. при сложении или вычитании векторов
складываются или вычитаются их одноименные
координаты;
},
т.е. при сложении или вычитании векторов
складываются или вычитаются их одноименные
координаты;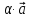 = {
= {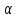 ·
·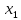 ;
;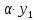 },
т.е. при умножении вектора на число его
координаты умножаются на это число.
},
т.е. при умножении вектора на число его
координаты умножаются на это число.
Условие коллинеарности двух векторов
Теорема
4. Вектор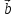 коллинеарен ненулевому вектору
коллинеарен ненулевому вектору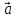 в том и только том случае, когда координаты
вектора
в том и только том случае, когда координаты
вектора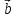 пропорциональны соответственным
координатам вектора
пропорциональны соответственным
координатам вектора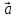 т.е.
т.е.
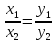 .
.
Линейные операции над векторами, заданными своими координатами в пространстве, производятся аналогично.
Пример
1. Пусть даны векторы = {1;2;-1} ,
= {1;2;-1} , = {3;2;1},
= {3;2;1},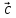 = {1;0;1} в некотором векторном базисе
= {1;0;1} в некотором векторном базисе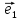 ,
, ,
,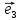 .
Найти координаты линейной комбинации
2
.
Найти координаты линейной комбинации
2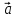 +3
+3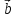 -4
-4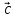 .
.
Решение.
Введем обозначение для линейной
комбинации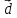 =2
=2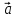 +3
+3 +(-4)
+(-4)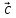 .
.
Коэффициенты
линейной комбинации
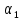 =2,
=2,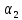 =3,
=3, =-4.
Запишем данное векторное равенство в
координатной форме
=-4.
Запишем данное векторное равенство в
координатной форме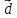 =
{x,y,z}=
=
{x,y,z}=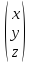 :
:
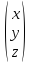 =2
=2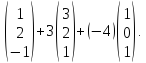
Очевидно, что каждая координата линейной комбинации векторов равна такой же линейной комбинации одноименных координат, т.е.
х = 2·1+3·3+(-4)·1=7,
у = 2·2+3·2+(-4)·0=10,
z= 2·(-1)+3·1+(-4)·0=-3.
Координаты
вектора
 в базисе
в базисе
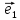 ,
,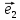 ,
,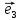 будут:
будут:
 =
{7,10,-3}
=
{7,10,-3}
Ответ: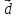 =
{7,10,-3}.
=
{7,10,-3}.
Общая (аффинная) декартова система координат
Определение 7. Пусть О- некоторая фиксированная точка, которую будем называтьначалом.
Если
М- произвольная точка, то вектор
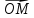 называетсярадиус-векторомточки
М по отношению к началу, коротко,
радиус-вектор точки М.
называетсярадиус-векторомточки
М по отношению к началу, коротко,
радиус-вектор точки М.
Декартовы (аффинные) координаты на прямой
Пусть
дана в пространстве некоторая прямая
l.Выберем начало
О лежащим на этой прямой. Кроме того,
выберем на прямойl
ненулевой вектор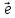 ,
который будем называть базисным.
,
который будем называть базисным.

Определение
8. Пусть точка М лежит на прямойl.
Так как векторы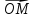 и
и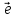 коллинеарны, то
коллинеарны, то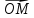 =х
=х ,
где х- некоторое число. Это число назовемкоординатой точки М на прямой.
,
где х- некоторое число. Это число назовемкоординатой точки М на прямой.
Начало
О имеет положительные или отрицательные
координаты, в зависимости от того,
совпадают ли направления векторов
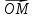 и
и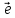 или они противоположны. Прямуюl,
на которой координаты, будем называть
осью координат или осью ОХ.
или они противоположны. Прямуюl,
на которой координаты, будем называть
осью координат или осью ОХ.
Введение координат на прямой соответствует единственное число х, и наоборот, существует единственная точка М, для которой это число является координатой.
Декартовы (аффинные) координаты на плоскости.
Выберем
на плоскости О два неколлинеарных
вектора
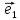 и
и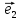 ,
образующих некоторый базис . Очевидно,
что длины векторов
,
образующих некоторый базис . Очевидно,
что длины векторов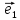 и
и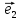 могут быть различны.
могут быть различны.
Определение
9. Совокупность {0;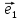 ;
;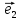 }
точки О и векторного базиса
}
точки О и векторного базиса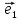 ,
, называют
декартовой (аффинной) системой на
плоскости.
называют
декартовой (аффинной) системой на
плоскости.
Две
прямые, проходящие через О и параллельные
соответственно векторам
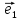 ,
,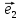 называют
осями координат. Первую из них обычно
называют осью абсцисс и обозначают Ох,
вторую- осью ординат и обозначают Оу.
называют
осями координат. Первую из них обычно
называют осью абсцисс и обозначают Ох,
вторую- осью ординат и обозначают Оу.
Будем
всегда изображать
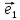 и
и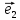 лежащими на соответствующих осях
координат.
лежащими на соответствующих осях
координат.

Определение
10. Координатами точки М на плоскости
относительно декартовой (аффинной)
системы координат {0;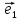 ;
;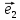 }
называют координаты ее радиус-вектора
}
называют координаты ее радиус-вектора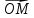 по базису
по базису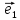 ,
,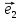 :
:
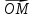 =
х
=
х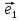 +у
+у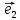 ,
тогда числа х и у будет координатами М
относительно декартовой(аффинной)
системы координат {0;
,
тогда числа х и у будет координатами М
относительно декартовой(аффинной)
системы координат {0;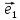 ;
;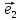 }.
Координату х называютабсциссой точки
М, координату у-ординатой точки М.
}.
Координату х называютабсциссой точки
М, координату у-ординатой точки М.
Итак,
если выбрана система координат, {0;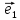 ;
;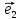 }
на плоскости, то каждой точке М плоскости
соответствует единственная точка М на
плоскости: эта точка является концом
вектора
}
на плоскости, то каждой точке М плоскости
соответствует единственная точка М на
плоскости: эта точка является концом
вектора
 =
х
=
х +у
+у .
.
Введение системы координат лежит в основе метода аналитической геометрии, сущность которой состоит в том, чтобы уметь сводить любую геометрическую задачу к задачам арифметики или алгебры.
Определение
11. Координатами вектора
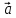 на
плоскости относительно декартовой
системы координат {0;
на
плоскости относительно декартовой
системы координат {0;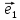 ;
;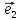 }
называют координаты этого вектора в
базисе
}
называют координаты этого вектора в
базисе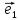 ,
,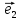 .
.
Чтобы
найти координаты вектора
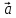 ,
надо разложить его по базису
,
надо разложить его по базису
 ,
,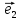 :
:
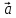 =
х
=
х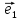 +у
+у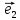 ,
где коэффициенты х,у и будут координатами
вектора
,
где коэффициенты х,у и будут координатами
вектора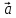 относительно декартовой системы {0;
относительно декартовой системы {0; ;
; }.
}.
Декартова (аффинная) система координат в пространстве.
Пусть в пространстве зафиксирована некоторая точка О(начало) и выбран векторный базис
 ,
,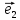 ,
,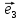 .
.
Определение
12. Совокупность {0;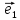 ;
;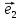 ;
;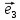 }называютдекартовой системой координат в
пространстве.
}называютдекартовой системой координат в
пространстве.
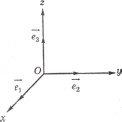
Определение
13. Три прямые проходящие через О и
параллельные соответственно векторам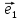 ,
,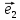 ,
,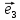 ,
называютосями координат и обозначают
соответственно Оz,Oy,Oz.Мы
будем всегда изображать векторы
,
называютосями координат и обозначают
соответственно Оz,Oy,Oz.Мы
будем всегда изображать векторы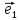 ,
,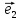 ,
,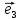 лежащими на соответственных осях.
лежащими на соответственных осях.
Определение
14. Координатами точки М в пространстве
относительно декартовой системы
координат {0;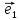 ;
;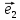 ;
;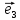 }
называют координаты ее радиус-вектора
}
называют координаты ее радиус-вектора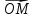 в этой системе.
в этой системе.
Иначе говоря, координаты точки М – это такие три числа х,у,zсоответственно абсцисса и ордината точки М; третью координатуzназывают аппликатой точки М.
Введение в пространстве декартовой системы координат позволяет установить взаимно-однозначное соответствие между точками М пространства и упорядоченными тройками чисел x,y,z.
Определение
15. Координатами вектора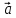 в пространстве относительно декартовой
системы координат {0;
в пространстве относительно декартовой
системы координат {0;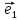 ;
;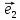 ;
;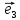 }называют
координаты этого вектора в базисе
}называют
координаты этого вектора в базисе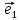 ;
;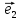 ;
;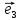 .
.
Пример 2.
Даны три последовательные вершины параллелограмма А(-2;1),В(1;3),С(4;0). Найти четвертую его координату D. Система координат аффинная.
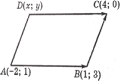
Решение.
Векторы
 и
и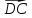 равны, значит, равны их координаты (
коэффициенты линейной комбинации):
равны, значит, равны их координаты (
коэффициенты линейной комбинации):
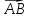 =
{3;2},
=
{3;2},
 ={4-x;-y};
={4-x;-y}; .
Значит,D(1;-2).
.
Значит,D(1;-2).
Ответ:D(1;-2).
Линейная зависимость. Понятие базиса
Определение
16. Векторы
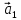 ,
,
 называют
линейно зависимыми, если
существуют числа
называют
линейно зависимыми, если
существуют числа
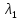 ,
,
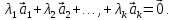 (***)
(***)
Это
определение линейной зависимости
векторов
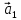 ,
,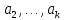 эквивалентно
такому: векторы
эквивалентно
такому: векторы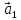 ,
,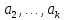 линейно зависимы, если один из них можно
представить в виде линейной комбинации
остальных (или разложить по остальным).
линейно зависимы, если один из них можно
представить в виде линейной комбинации
остальных (или разложить по остальным).
Векторы
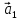 ,
,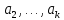 называются линейно зависимыми, если
равенство (***) возможно в единственном
случае, когда
называются линейно зависимыми, если
равенство (***) возможно в единственном
случае, когда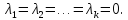
Понятие линейной зависимости играет большую роль в линейной алгебре. В векторной алгебре линейная зависимость имеет простой геометрический смысл.
Любые два коллинеарных вектора линейно зависимы, и наоборот, два неколлинеарных вектора линейно независимы.
Три компланарных вектора линейно зависимы, и наоборот, три некомпланарных вектора линейно независимы.
Каждые четыре вектора линейно зависимы.
Определение
17. Три линейно
независимых вектора
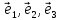 называютсябазисом
пространства, т.е.
любой вектор
называютсябазисом
пространства, т.е.
любой вектор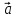 может быть представлен в виде некоторой
может быть представлен в виде некоторой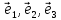 .
.
Определение
18. Два лежащих
в плоскости линейно независимых вектора
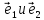 называютбазисом
плоскости, т.е.
любой лежащий в этой плоскости вектор
называютбазисом
плоскости, т.е.
любой лежащий в этой плоскости вектор
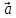 может быть представлен в виде линейной
комбинации векторов
может быть представлен в виде линейной
комбинации векторов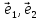 .
.
Задания для самостоятельного решения.
Даны три вектора
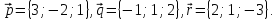 Найти
разложение вектора
Найти
разложение вектора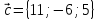 по
базису
по
базису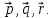
Даны векторы
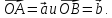 Вектор
Вектор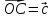 –медиана
треугольникаOAB.
Разложить вектор
–медиана
треугольникаOAB.
Разложить вектор
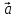 по
базису
по
базису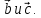
В тетраэдре OABC точки K, L, M, N, P, Q – середины рёбер OA, OB, OC, AB, AC, BC соответственно, S – точка пересечения медиан треугольника ABC. Принимая за базисные
векторы
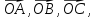 найти в этом базисе координаты:
найти в этом базисе координаты:
векторов

векторов
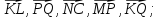
векторов
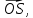 и
и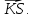
Точки Mи N – середины сторон BCи CDпараллелограмма ABCD. Разложить вектор
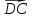 по
векторам
по
векторам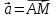 и
и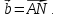
Дан куб ABCDEFGH. Разложить вектор
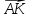 ,
гдеK–
центр грани DHGC,
по векторам
,
гдеK–
центр грани DHGC,
по векторам
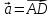 ,
,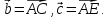
На плоскости даны вектора
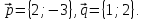 Найти
разложение вектора
Найти
разложение вектора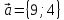 по
базису
по
базису ,
,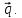
На плоскости даны три вектора
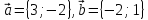 и
и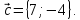 Определить разложение каждого из этих
трёх векторов, принимая в качестве
базиса два других.
Определить разложение каждого из этих
трёх векторов, принимая в качестве
базиса два других.Принимая в качестве базиса векторы
 и
и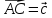 ,
совпадающие со сторонами треугольникаABC,
определить разложение векторов,
приложенных в вершинах треугольника
и совпадающих с его медианами.
,
совпадающие со сторонами треугольникаABC,
определить разложение векторов,
приложенных в вершинах треугольника
и совпадающих с его медианами.Даны четыре вектора
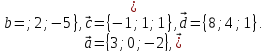 Найти координаты векторов – линейных
комбинаций:
Найти координаты векторов – линейных
комбинаций: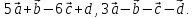
Даны четыре вектора
 ,
,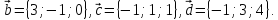 Найти числа α, β, γ такие, что α
Найти числа α, β, γ такие, что α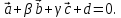
Проверить, что векторы
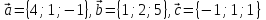 образуют базис в пространстве. Найти
координаты векторов
образуют базис в пространстве. Найти
координаты векторов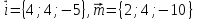 ,
,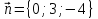 в
этом базисе.
в
этом базисе.(Задача об отрезке, разделённом в заданном отношении.) Пусть точка C, лежащая на отрезкеAB, делит этот отрезок в отношении λ, т.е.
 Выразить вектор
Выразить вектор через векторы
через векторы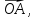 и
и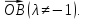
Даны две точки A(1;2;3). B(7;2;5). На прямой ABнайти такую точку M, чтобы точки Bи Mбыли расположены по разные стороны от точки A и чтобы отрезок AMбыл вдове длиннее отрезка AB. Система координат аффинная.
Вершина Aпараллелепипеда ABCD
 принята за начало координат, а векторы
принята за начало координат, а векторы
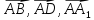 – за базисные векторы. Найти в этой
системе координаты всех вершин
параллелепипеда.
– за базисные векторы. Найти в этой
системе координаты всех вершин
параллелепипеда.Вершина Oтетраэдра OABCDпринята за начало координат, а векторы
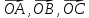 – за базисные векторы. Найти на этой
(аффинной) системе координаты точек
пересечения медиан граней тэтраэдра.
– за базисные векторы. Найти на этой
(аффинной) системе координаты точек
пересечения медиан граней тэтраэдра.
