
- •Самарина е.Ф.
- •Оглавление
- •§3. Прямоугольная декартова система координат . . . . . . . . . . . . . . . . . . . . . . . . . .30
- •§4. Скалярное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32
- •§5. Векторное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34
- •§6. Смешанное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .37
- •Предисловие в учебное пособие вошли все разделы стандартного курса математики содержащихся в первом семестре.
- •§1. Определители и матрицы
- •§2. Линейное (векторное) пространство.
- •§3. Cистемы линейных алгебраических уравнений.
- •§2.Линейные операции над векторами.
- •§2 Линейная комбинация векторов
- •§3. Прямоугольная декартова система координат
- •§4.Скалярное произведение векторов.
- •§5. Векторное произведение векторов.
- •§6.Смешанное произведение векторов
- •Решение системы находим по формулам Крамера
- •Вариант 1
- •Вариант 11
- •Вопрос 1. Что такое матрица?
§5. Векторное произведение векторов.
Определение
1.Векторным произведением двух
векторов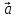 и
и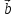 называют третий вектор
называют третий вектор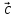 ,
удовлетворяющий условиям:
,
удовлетворяющий условиям:
1)
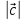 =
=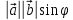 , где-угол между
, где-угол между и
и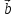 (0
(0 );
);
2)
вектор
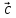 ортогонален векторам
ортогонален векторам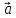 и
и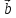 ,
т.е.
,
т.е.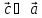 и
и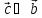 ;
;
3)векторы
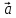 ,
,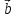 ,
,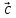 образуют правую тройку векторов.
образуют правую тройку векторов.
Векторное
произведение векторов
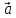 и
и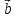 обозначают
обозначают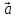 х
х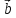 или [
или [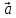 x
x ].
].
Если
хотя бы один из сомножителей равен
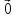 ,
то векторное произведение по определению
есть нулевой вектор.
,
то векторное произведение по определению
есть нулевой вектор.
Понятие
векторного произведения родилось в
механике. Если вектор
 =
=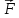 изображает
приложенную в некоторой точке Р силу ,
а вектор
изображает
приложенную в некоторой точке Р силу ,
а вектор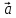 идет из некоторой точки О в точку Р, то
вектор
идет из некоторой точки О в точку Р, то
вектор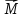 =[
=[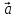 x
x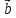 ]
=
]
=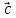 представляет собой момент силы
представляет собой момент силы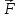 относительно
точки О.
относительно
точки О.
Геометрический смысл векторного произведения.
1. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
2.
Длина( модуль) векторного произведения
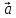 х
х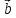 равна площадиSпараллелограмма,
построенного на приведенных к общему
началу векторах
равна площадиSпараллелограмма,
построенного на приведенных к общему
началу векторах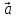 и
и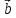 ,
т.е.
,
т.е.
S=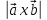 =
=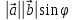 ,
,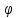 =(
=(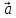 ,
,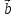 ).
).
Алгебраические свойства векторного произведения.
Векторное умножение обладает следующими четырьмя свойствами:
1)[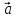 x
x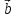 ]=-[
]=-[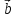 х
х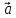 ]
(свойство антикоммутативности);
]
(свойство антикоммутативности);
2)
[(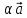 )х
)х ]=
]= [
[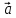 х
х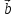 ]
(свойство ассоциативности относительно
числового множителя);
]
(свойство ассоциативности относительно
числового множителя);
3)
[( +
+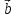 )х
)х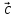 ]
= [(
]
= [( x
x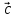 )]+[
)]+[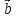 x
x ]
(свойство дистрибутивности относительно
суммы векторов);
]
(свойство дистрибутивности относительно
суммы векторов);
4)
[(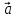 х
х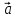 )]
=
)]
=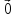 для
любого вектора
для
любого вектора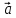 .
.
Если
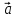 = {
= {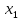 ;
;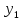 ;
;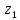 }
и
}
и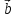 = {
= {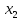 ;
;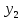 ;
;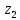 }
– векторы, заданные своими координатами
в пямоугольном базисе, то разложение
векторного произведения [
}
– векторы, заданные своими координатами
в пямоугольном базисе, то разложение
векторного произведения [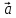 x
x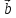 ]
в том же базисе имеет вид:
]
в том же базисе имеет вид:
[ x
x ]
=
]
=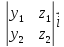 -
-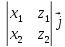 +
+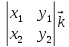 ,
или
,
или х
х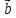 =
=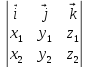 .
.
Пример
1. Доказать, что (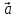 -
-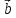 )x(
)x(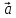 +
+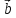 )
= 2
)
= 2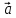 x
x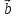 ,
и выяснить геометрическое значение
этого тождества.
,
и выяснить геометрическое значение
этого тождества.
Решение.
(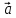 -
-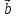 )
х (
)
х (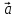 +
+ )
=
)
=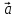 х
х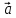 + (
+ (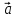 х
х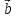 )
– (
)
– (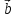 х
х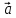 )
– (
)
– (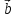 х
х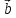 ).
Так как
).
Так как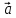 х
х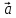 =
= ,
,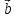 х
х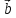 =
=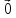 ,
,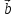 х
х = -[
= -[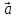 х
х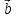 ],
то получаем
],
то получаем
( -
-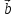 )x(
)x(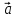 +
+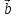 )
=2[
)
=2[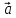 x
x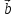 ]
и
]
и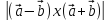 = 2
= 2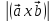 .
Это с геометрической точки зрения
означает: площадь параллелограмма,
построенного на диагоналях данного
параллелограмма, вдвое больше площади
данного параллелограмма.
.
Это с геометрической точки зрения
означает: площадь параллелограмма,
построенного на диагоналях данного
параллелограмма, вдвое больше площади
данного параллелограмма.
Задания для самостоятельного решения.
1.
Найти векторное произведение векторов
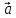 и
и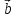 ,
заданных своими координатами.
,
заданных своими координатами.
1)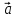 ={3;-1;2},
={3;-1;2},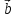 ={2;-3;5};
={2;-3;5};
2)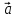 ={2;-1;1},
={2;-1;1}, ={-4;2;2};
={-4;2;2};
3)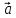 ={6;1;0},
={6;1;0},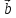 ={3;-2;0};
={3;-2;0};
2. Упростить выражения:
1)[
(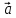 +
+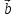 )x(
)x(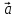 -
-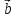 )];
2) [(
)];
2) [(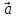 -
-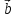 +
+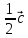 )x(
)x(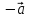 +2
+2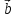 -5
-5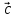 )].
)].
3.Векторы
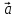 и
и неколлинеарны. При каких значениях λ
коллинеарны векторы λ
неколлинеарны. При каких значениях λ
коллинеарны векторы λ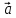 +
+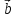 и 3
и 3 +λ
+λ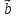 ?
?
4.На
векторах
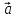 ={2;3;1}
и
={2;3;1}
и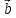 ={-1;1;2}, отложенных от одной точки, построено
треугольник. Найти:
={-1;1;2}, отложенных от одной точки, построено
треугольник. Найти:
1) площадь этого треугольника;
2)длины трех его высот.
5. Раскрыть скобки и упростить выражения:
1)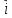 x(
x(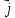 +
+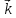 )-
)-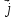 x(
x( +
+ )
+
)
+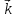 x(
x( +
+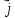 -
-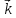 );
);
2)(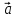 +
+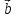 +
+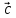 )xc+(
)xc+(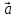 +
+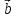 +
+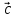 )x
)x +(
+(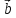 -
-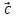 )x
)x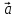 ;
;
3)(2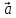 +
+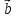 )x(
)x( -
- )+(
)+(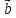 +
+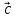 )x(
)x( +
+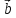 );
);
4)
2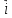 x(
x(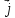 x
x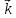 )+3
)+3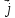 x(
x(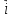 x
x )+4
)+4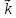 x(
x(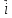 x
x ).
).
6. Даны точки А(2;-1;2), B(1;2;-1) иC(3;2;1). Найти координаты векторных произведений:
1)
[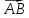 x
x ];
2)[(
];
2)[(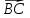 -2
-2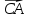 )x
)x ].
].
7.
Векторы
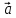 и
и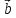 ортогональны. Зная, что
ортогональны. Зная, что =3,
=3, =4,
вычислить:
=4,
вычислить:
1)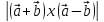 ;
2)
;
2)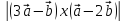 .
.
8.
Даны векторы
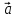 = {3;-1;-2} и
= {3;-1;-2} и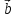 = {1;2;-1}.
= {1;2;-1}.
Найти координаты векторных произведений:
1)
[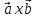 ];
2)[(2
];
2)[(2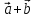 )x
)x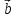 ];
3) [(2
];
3) [(2 )x(2
)x(2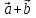 )].
)].
9.Даны точки А(1;2;0), B(3;0;-3) иC(5;2;6).
Вычислить площадь треугольника ABC.
10.
Вектор x, перпендикулярный
к векторам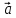 ={4;-2;-3}
и
={4;-2;-3}
и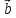 =
{0;1;3} Образует с осью Оу тупой угол. Зная,
что
=
{0;1;3} Образует с осью Оу тупой угол. Зная,
что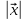 =26,
найти его координаты.
=26,
найти его координаты.
11.
Векторы
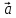 и
и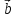 образуют угол
образуют угол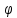 =
=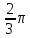 .
Зная, что
.
Зная, что =1,
=1,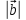 =2,
вычислить:
=2,
вычислить:
1)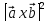 ;
2)
;
2)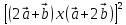 ;
3)
;
3)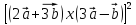 .
.
12. Вычислить синус угла, образованного векторами
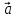 ={2;-2;1}
и
={2;-2;1}
и
 =
{2;3;6}.
=
{2;3;6}.
13. Даны вершины треугольника А(1;-1;2), B(5;-6;2) иC(1;3;-1). Вычислить длину его высоты, опущенной из вершиныBна сторону АС.
14.
Сила
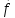 ={3;2;-4}
приложена к точке А(2;-1;1). Определить
момент этой силы относительно начала
координат.
={3;2;-4}
приложена к точке А(2;-1;1). Определить
момент этой силы относительно начала
координат.
15.
Сила
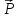 = {2;-4;5} приложена к точке
= {2;-4;5} приложена к точке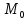 (4;-2;3).
Определить момент этой силы относительно
точки А (3;2;-1).
(4;-2;3).
Определить момент этой силы относительно
точки А (3;2;-1).
16.
Сила
 = {3;4;-2} приложена к точке
= {3;4;-2} приложена к точке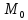 (2;-1;-2).
Определить величину и направляющие
косинусы момента этой силы относительно
начала координат.
(2;-1;-2).
Определить величину и направляющие
косинусы момента этой силы относительно
начала координат.
17. Найти площадь треугольника с вершинами в точках А(0;1), B(4;5) иC(6;-1).
18.
Найти площадь параллелограмма,
построенного на векторах
 = 2
= 2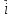 +
+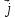 +3
+3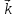 и
и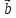 =
= +
+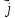 +
+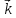 .
.
19. Найти площадь треугольника с вершинами А(-1;2;3), B(2;1;4) иC(0;-3;4).
20.
Определить, при каких значениях
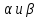 вектор
вектор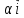 +3
+3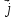 +
+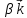 будет коллинеарен вектору [
будет коллинеарен вектору [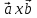 ],
если
],
если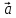 =
{3;-1;1},
=
{3;-1;1},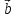 ={1;2;0}.
={1;2;0}.
21. Вычислить площадь треугольника с вершинами А(7;3;4), B(1;0;6),C(4;5;-2).
