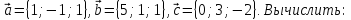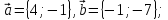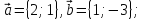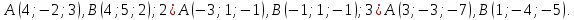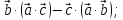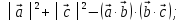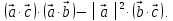- •Самарина е.Ф.
- •Оглавление
- •§3. Прямоугольная декартова система координат . . . . . . . . . . . . . . . . . . . . . . . . . .30
- •§4. Скалярное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32
- •§5. Векторное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34
- •§6. Смешанное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .37
- •Предисловие в учебное пособие вошли все разделы стандартного курса математики содержащихся в первом семестре.
- •§1. Определители и матрицы
- •§2. Линейное (векторное) пространство.
- •§3. Cистемы линейных алгебраических уравнений.
- •§2.Линейные операции над векторами.
- •§2 Линейная комбинация векторов
- •§3. Прямоугольная декартова система координат
- •§4.Скалярное произведение векторов.
- •§5. Векторное произведение векторов.
- •§6.Смешанное произведение векторов
- •Решение системы находим по формулам Крамера
- •Вариант 1
- •Вариант 11
- •Вопрос 1. Что такое матрица?
§3. Прямоугольная декартова система координат
Среди декартовых систем координат простейшей является прямоугольная декартова система координат.
Определение
1. Декартова
система координат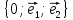 на
плоскости называется прямоугольной,
если
на
плоскости называется прямоугольной,
если
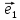 и
и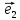 – ортогональные единичные векторы.
– ортогональные единичные векторы.
Аналогично
определяется прямоугольная декартова
система координат
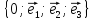 в
пространстве; в этом случае векторы
в
пространстве; в этом случае векторы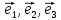 также
являются взаимно перпендикулярными и
единичными. Базисные векторы
также
являются взаимно перпендикулярными и
единичными. Базисные векторы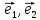 прямоугольной декартовой системы
координат на плоскости обозначают
обычно
прямоугольной декартовой системы
координат на плоскости обозначают
обычно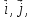 базисные
векторы
базисные
векторы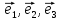 прямоугольной
декартовой системы координат обозначают
прямоугольной
декартовой системы координат обозначают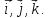 Соответственно разложение радиус-вектора
Соответственно разложение радиус-вектора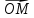 по базису записывают в виде
по базису записывают в виде
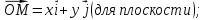
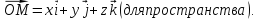
Определение
2. Проекцией
вектора
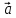 на единичный вектор
на единичный вектор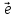 называется
число
называется
число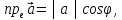 где
где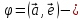 угол
между векторами
угол
между векторами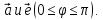
Координаты
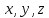 вектора
вектора полученные как коэффициенты линейной
комбинации базисных векторов, в
прямоугольном базисе совпадают с
проекцией вектора
полученные как коэффициенты линейной
комбинации базисных векторов, в
прямоугольном базисе совпадают с
проекцией вектора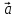 на базисные орты
на базисные орты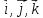 соответственно, а длина вектора
соответственно, а длина вектора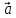 равна
равна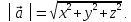
Определение
3. Числа
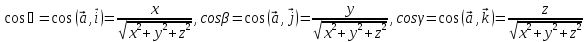 называетсянаправляющими
косинусами вектора
называетсянаправляющими
косинусами вектора
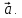
Направляющие
косинусы вектора совпадают с координатами
(проекциями) его орта
 и между собой связаны соотношением
и между собой связаны соотношением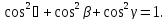
Отметим,
что базис
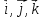 называют ортонормированным, так как
называют ортонормированным, так как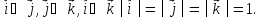
Пример
1. Заданы
векторы
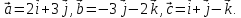 Найти:
Найти:
а)
координаты вектора
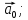
б)
координаты вектора
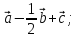
в)
разложение вектора
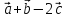 по
базису
по
базису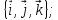
г)
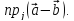
Решение.
а)
Так как
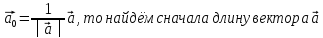 по формуле│
по формуле│
│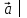 =
=
 Тогда
Тогда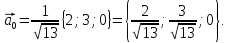
б)
Вычислим координаты вектора
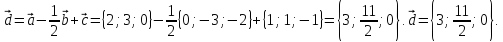
в)
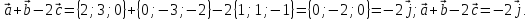
г)
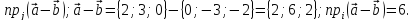
Ответ:

б)
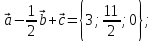
в)
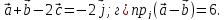
Замечание.
Если известны
координаты точек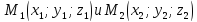 ,
то проекцииX,
Y,
Z
на оси координат вектора
,
то проекцииX,
Y,
Z
на оси координат вектора
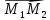 могут быть получены по формулам
могут быть получены по формулам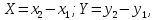
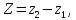 то
расстояние d
между данными точками определяется
формулой:
то
расстояние d
между данными точками определяется
формулой:

Если
точка
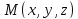 лежит
на прямой, проходящей через две данные
точки
лежит
на прямой, проходящей через две данные
точки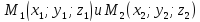 и дано отношение
и дано отношение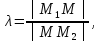 в котором точкаM
делит отрезок
в котором точкаM
делит отрезок
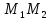 ,
то координаты точкиM
определяются по формулам:
,
то координаты точкиM
определяются по формулам:
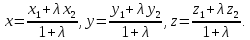
§4.Скалярное произведение векторов.
Рассмотрим
следующую задачу. Материальная точка
массой 1кг под действием постоянной по
величине и направлению силы
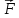 переместилась вдоль прямой из точки P
в точку Q.
Какая при этом совершилась работа? Как
известно из физики, работа равна
произведению силы на перемещение и на
косинус угла между направлениями силы
и перемещения. Применяя векторные
обозначения, можно записать:
переместилась вдоль прямой из точки P
в точку Q.
Какая при этом совершилась работа? Как
известно из физики, работа равна
произведению силы на перемещение и на
косинус угла между направлениями силы
и перемещения. Применяя векторные
обозначения, можно записать:
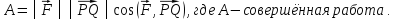
Определение
1. Скалярным
произведением двух
ненулевых векторов
 называется число, равное
называется число, равное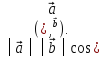
Если
хотя бы один из векторов
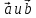 равен нулю, то их скалярное произведение
принимают равным нулю. Скалярное
произведение векторов
равен нулю, то их скалярное произведение
принимают равным нулю. Скалярное
произведение векторов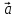 и
и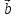 обозначают
обозначают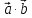 или (
или (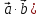 .
Итак,
.
Итак,
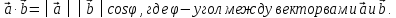
Скалярное
произведение векторов
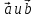 можно
выразить также формулой
можно
выразить также формулой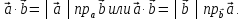 Здесь
Здесь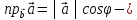 проекция
вектора
проекция
вектора на
ось вектора
на
ось вектора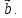
Из
определения следует, что
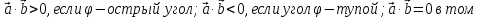 случае, когда векторы
случае, когда векторы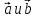 перпендикулярны
(ортогональны),
перпендикулярны
(ортогональны),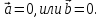
Отметим
ещё факт. Скалярное произведение
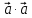 вектора
вектора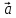 на себя называют скалярным квадратом
вектора
на себя называют скалярным квадратом
вектора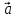 и обозначают
и обозначают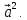 Так как в этом случае угол
Так как в этом случае угол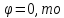
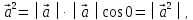
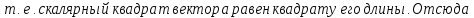 следует,
что │
следует,
что │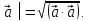
Свойства скалярного произведения.
Скалярное умножение коммутативно, т.е. для любых векторов
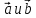 справедливо равенство
справедливо равенство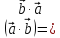 )
) ненулевой
вектор, и
ненулевой
вектор, и
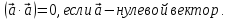
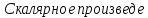 ние
равно нулю тогда и только тогда, когда
сомножители ортогональны или хотя бы
один из них равен нуль-вектору.
ние
равно нулю тогда и только тогда, когда
сомножители ортогональны или хотя бы
один из них равен нуль-вектору.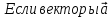 и
и
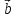 заданы своими координатами в ортогональном
базисе
заданы своими координатами в ортогональном
базисе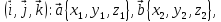 то их скалярное произведение может
быть вычислено по формуле
то их скалярное произведение может
быть вычислено по формуле
Отсюда
следует необходимое и достаточное
условие ортогональности векторов: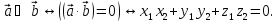
Для любых векторов
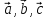 справедливо равенство
справедливо равенство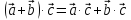 (дистрибутивность
операции сложения относительно операции
умножения векторов).
(дистрибутивность
операции сложения относительно операции
умножения векторов).Для любых векторов
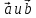 и любого числаk
справедливо равенство
и любого числаk
справедливо равенство
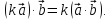 (Ассоциативность по отношению к
умножению вектора на число.)
(Ассоциативность по отношению к
умножению вектора на число.)Пусть
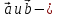 два
ненулевых вектора,
два
ненулевых вектора, угол между ними. Из определения скалярного
произведения следует:
угол между ними. Из определения скалярного
произведения следует: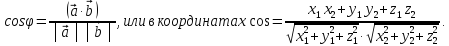
Пусть в пространстве дана некоторая ось
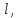 единичный вектор
единичный вектор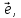 который составляет с координатными
осями углы
который составляет с координатными
осями углы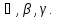 Тогда
проекция произвольного вектора
Тогда
проекция произвольного вектора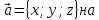 эту
ось определяется формулой
эту
ось определяется формулой
Пример
1. Найти проекцию
вектора
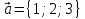 на ось
на ось ,
образующую с координатными осями острые
углы.
,
образующую с координатными осями острые
углы.
Решение.
Направляющие
косинусы оси
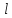 таковы:
таковы: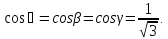
Следовательно,
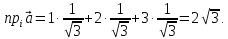
Ответ:
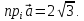
Пример
2. Даны векторы
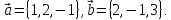 Найти
Найти
Решение.
Так как
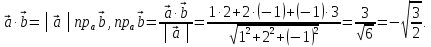
Ответ:
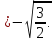
Задания для самостоятельного решения
Раскрыть скобки в выражении
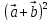 и выяснить геометрический смысл
полученной формулы.
и выяснить геометрический смысл
полученной формулы.Даны три вектора
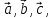 удовлетворяющие условию
удовлетворяющие условию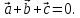 Зная, что
Зная, что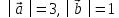 и
и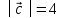 ,
вычислить
,
вычислить
Векторы
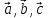 попарно образуют друг с другом углы,
каждый из которых равен 60
попарно образуют друг с другом углы,
каждый из которых равен 60 .
Зная, что
.
Зная, что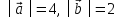 и
и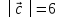 ,
определить модуль вектора
,
определить модуль вектора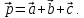
Какому условию должны удовлетворять векторы
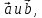 чтобы вектор
чтобы вектор был ортогонален вектору
был ортогонален вектору
Доказать, что векторы
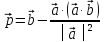 ортогонален вектору
ортогонален вектору
Даны векторы
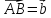 и
и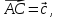 совпадающие со сторонами треугольникаABC.
Найти разложение по базису
совпадающие со сторонами треугольникаABC.
Найти разложение по базису
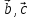 вектора, приложенного к вершинеB
этого треугольника и совпадающего с
его высотой BD.
вектора, приложенного к вершинеB
этого треугольника и совпадающего с
его высотой BD.Даны векторы
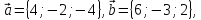 вычислить:
вычислить:
Дан равносторонний треугольник ABC, длины которого равны 1. Вычислить выражение
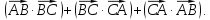
В треугольнике ABCданы длины его сторон:
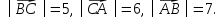 Найти скалярные произведения векторов
Найти скалярные произведения векторов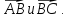
В треугольнике ABCпроведены медианы
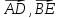 и
и Вычислить
Вычислить
Найти скалярное произведение векторов
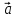 и
и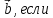
│
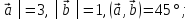
│

│

│
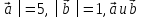 соноправлены;
соноправлены;│
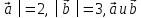 противоположно
направлены.
противоположно
направлены.
Вычислить выражение │
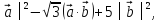 если:
если:
│
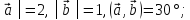
│
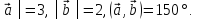
Найти скалярное произведение векторов
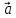 и
и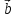 ,
заданных своими координатами:
,
заданных своими координатами:
Найти расстояние между точками Aи B, заданными своими координатами:
Даны три вектора: