- •Самарина е.Ф.
- •Оглавление
- •§3. Прямоугольная декартова система координат . . . . . . . . . . . . . . . . . . . . . . . . . .30
- •§4. Скалярное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .32
- •§5. Векторное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .34
- •§6. Смешанное произведение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .37
- •Предисловие в учебное пособие вошли все разделы стандартного курса математики содержащихся в первом семестре.
- •§1. Определители и матрицы
- •§2. Линейное (векторное) пространство.
- •§3. Cистемы линейных алгебраических уравнений.
- •§2.Линейные операции над векторами.
- •§2 Линейная комбинация векторов
- •§3. Прямоугольная декартова система координат
- •§4.Скалярное произведение векторов.
- •§5. Векторное произведение векторов.
- •§6.Смешанное произведение векторов
- •Решение системы находим по формулам Крамера
- •Вариант 1
- •Вариант 11
- •Вопрос 1. Что такое матрица?
§2. Линейное (векторное) пространство.
Определение
1. Совокупностьnдействительных
чисел ,
, ,…,
,…, ,
заданных в определенном порядке,
называетсяn-мерным
вектором. Числа
,
заданных в определенном порядке,
называетсяn-мерным
вектором. Числа ,
, ,…,
,…, называются координатами вектора.
называются координатами вектора.
Над n-мерными векторами вводятся следующие операции.
Сложение:
если x=( ,
, ,…,
,…, ),y=
),y= ,
, ,…,
,…, ),
тоx+y=(
),
тоx+y=( +
+ ,
, +
+ ,
… ,
,
… , +
+ ).
).
Умножение
на число : если
 -
действительное число иx=(
-
действительное число иx=( ,
, ,…,
,…, )-вектор,
то
)-вектор,
то x=(
x=( ,
, ,
…,
,
…, ).
).
Определение 2. Два вектора называютсяравными, если равны их соответствующие координаты
( ,
,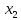 ,…,
,…, )
=
)
= ,
, ,…,
,…, )
) =
= ,
,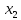 =
= ,
… ,
,
… , =
= .
.
Среди n-мерных векторов есть вектор, нейтральный относительно операций сложения.
Этот вектор с нулевыми координатами. Его называют нулевым вектором и обозначают через 0:
0=(0,0,…,0).
Каждый вектор xимеет противоположный : его обозначают –x, причем
-x=( ,
, ,…,
,…, ).
).
Введенные операции сложения векторов и умножение вектора на число обладают восемью свойствами:
x+y=y+x
(x+y)+z=x+(y+z)
x+0=0
x+(-x)=0
λ(μx)=(λμ)x
λ(x+y)= λx+λy
(λ+μ)=λx+μx
1·x=x.
Определение
3. Множество всехn-мерных
векторов, для которых установлены
операции сложения и умножения на число,
называетсяn-мерным
векторным (линейным) пространством
Определение
4. Системаn-мерных
векторов { ,
, ,…,
,…, }
называетсялинейно зависимой, если
найдутся числа
}
называетсялинейно зависимой, если
найдутся числа ,
, ,…,
,…, ,
не равные одновременно нулю, такие, что
,
не равные одновременно нулю, такие, что +
+ +…+
+…+ =0.
=0.
В противном случае эта система называется линейно независимой .
Определение
5.ПустьQ- произвольное
множествоn-мерных векторов
пространства .
Система векторовB={
.
Система векторовB={ ,
, ,…,
,…, }
называетсябазисом вQ,
если выполняются следующие условия:
}
называетсябазисом вQ,
если выполняются следующие условия:
 Q,
k=1,2,…,s;
Q,
k=1,2,…,s;Система B={
 ,
, ,…,
,…, }
линейно независима;
}
линейно независима;Для любого вектора
 Qнайдутся
числа
Qнайдутся
числа ,
, ,…,
,…, ,
такие, чтоx=
,
такие, чтоx= .
.
Определение
6. Формула называется
разложением вектораxпо
базисуB=(
называется
разложением вектораxпо
базисуB=( ,
, ,…,
,…, ).
Коэффициенты
).
Коэффициенты ,
, ,…,
,…, однозначно определяются векторомxи
называются координатами этого вектора
в базисе В.
однозначно определяются векторомxи
называются координатами этого вектора
в базисе В.
Справедливы следующие утверждения:
Всякая система векторов Q
 имеет
по меньшей мере один базис; при этом
все базисы этой системы состоят из
одинакового числа векторов, называемого
рангом системыQ, и
обозначаютсяr(Q).
имеет
по меньшей мере один базис; при этом
все базисы этой системы состоят из
одинакового числа векторов, называемого
рангом системыQ, и
обозначаютсяr(Q).Ранг всего пространства
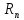 равенnи называется размерностью
этого пространства; при этом в качестве
базиса
равенnи называется размерностью
этого пространства; при этом в качестве
базиса можно
взять следующую систему:
можно
взять следующую систему:
 Этот
базис принято называть каноническим.
Этот
базис принято называть каноническим.
Зафиксируем
произвольный базис B=( ,
, ,
…,
,
…, )
в пространстве
)
в пространстве .
Тогда всякому векторуxможно поставить взаимно однозначное
соответствие столбец его координат в
этом базисе, т.е.
.
Тогда всякому векторуxможно поставить взаимно однозначное
соответствие столбец его координат в
этом базисе, т.е.
X= +
+ +…+
+…+ =
= .
.
§3. Cистемы линейных алгебраических уравнений.
Системы n линейныйх алгебраических уравнений с n неизвестными
Пусть дана система nлинейных алгебраических уравнений сnнеизвестными вида

Или
в матричной форме, АХ=b,
где А=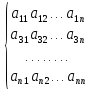 –матрица
системы,
–матрица
системы,
X= - матрица-столбец неизвестных,
- матрица-столбец неизвестных,
B= - матрица-столбец свободных членов
данной системы.
- матрица-столбец свободных членов
данной системы.
Правило Крамера
Если
в системе detA 0,
т.е. матрица А имеет обратную
0,
т.е. матрица А имеет обратную ,
то система имеет, и при этом единственное,
решениеX=
,
то система имеет, и при этом единственное,
решениеX= ·b,
или
·b,
или ,
i=1,2,…,n,
,
i=1,2,…,n,
где
 -определитель,
получаемый из определителя
-определитель,
получаемый из определителя системы
заменойi-го столбца на
столбец свободных членов.
системы
заменойi-го столбца на
столбец свободных членов.
Пример 1. Решить систему уравнений по правилу Крамера

Решение.
Определитель
системы
 =
= =5,
=5,
 =
= (2)+(1)=(3)+(1)=
(2)+(1)=(3)+(1)= =15,
=15,
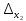 =
= =1·
=1· -5
-5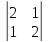 +1·
+1· =8-15+2=-5;
=8-15+2=-5;
 =
= (2)+(1)=(3)+(1)
(2)+(1)=(3)+(1) =(-1)·
=(-1)· =5.
=5.
Тогда

Ответ:

Произвольные системы линейных алгебраических уравнений. Теорема Кронекера-Капелли
Пусть дана система mлинейных уравнений сnнеизвестными общего вида
 (*)
(*)
Или в матричной форме, AX=b,
Где
А =
 – матрица системы, размераmxn,
– матрица системы, размераmxn,
X= – матрица-столбец неизвестных,
– матрица-столбец неизвестных,
B= – матрица-столбец свободных членов
данной системы.
– матрица-столбец свободных членов
данной системы.
Определение
1.Решением системы называется
такая совокупностьnчисел ,
, ,
…,
,
…, ,
что при подстановке их во все уравнения
системы вместо соответствующих
неизвестных получаются числовые
тождества.
,
что при подстановке их во все уравнения
системы вместо соответствующих
неизвестных получаются числовые
тождества.
Определение 2. Система, имеющая хотя бы одно решение, называетсясовместной; система, имеющая ни одного решения -несовместной.
Определение 3. Система, имеющая единственное решение, называетсяопределенной; система, имеющая более одного решения -неопределенной.
Определение 4. Две системы называются эквивалентными, если множества их решений совпадают.
Определение
5. Матрица (Alb) =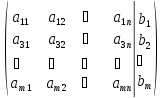 ,
,
Получаемая из матрицы А системы добавлением столбца свободных членов, называется расширенной матрицей.
Теорема 1. Для того, чтобы система (*) была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы, т.е.
r(A)=(Alb).
Иначе,
1) r(A) r(Alb)
r(Alb) система
несовместна,
система
несовместна,
2)r(A)=r(Alb) система
совместна,
система
совместна,
3)
r(A)=r(Alb)
=n система
определенна,
система
определенна,
4)
r(A)=r(Alb) n
n система
неопределенна.
система
неопределенна.
Алгоритм исследования произвольных система линейных уравнений методов Гаусса.
1) Сначала расширенная матрица (Alb) приводится с помощью элементарных преобразований к ступенчатому виду и матрица А системы (*));
2) затем находятся числа r(A) ,r(Alb) иn(n- число неизвестных системы);
3) проводится исследование системы согласно теоремы Кронекера-Капелли.
Пример 2. Исследовать систему.

Решение.
 =
(2)-5(1)
=
(2)-5(1) (3)-(1)
(3)-(1) (3)-3(2)
(3)-3(2)
(3)

r(A)=3,r(Alb)=3,n=3.
Отве: система совместна и имеет единственное решение.
Метод Гаусса
Определенные линейные алгебраические системы
Определение 6. Система являетсяопределенной тогда и только тогда, когдаr(A)=r(Alb)=n. В этом случае имеем системуnлинейных уравнений сnнеизменными, определитель которой не равен нулю. Значит, по формулам Крамера можно найти ее решение. Найдем же решение этой системы методом Гаусса. В этом случае матрица А после приведения её к ступенчатому виду будет треугольной, т.е. количество строк у нее равняется количеству столбцов ( так какr(A) =nи ниже диагонали расположены нули). С помощью элементарных преобразований матрицу А можно привести к единичной матрице, тогда после черты в расширенной матрице будет расположено решение системы, т.е. приведем расширенную матрицу к виду (ElX).
Пример 3.Найти решение системы уравнений примера 2 методом Гаусса.
Данную систему мы приведем к виду:
 .
С помощью элементарных преобразований
приведем матрицу А к единичному виду.
.
С помощью элементарных преобразований
приведем матрицу А к единичному виду.
 -
- (3)
(3) (2)-9(3)
(2)-9(3) (1)+(3)
(1)+(3) (2)
(2)
 (1)+(2)
(1)+(2) .
.
Следовательно,

Проверка. Подставим эти значения неизвестных в систему примера 2.
2-3-(-1)=0,5·2-1·3+4·(-1)=10-7=3,
1·2+2·3+3(-1)=8-3=5.
Ответ:
Неопределенные линейные алгебраические системы.
Если система имеет бесконечное множество решений, то все их перечислить невозможно. В этом случае строится общее решение системы.
Определение 7. Общим решением неопределенной системы называется такая система, эквивалентная исходной, в которой часть неизвестных, называемых зависимыми, выражена через остальные неизвестные, называемые независимыми.
Опишем способ нахождения общего решения системы, предполагая, что её матрица уже приведена к ступенчатому виду.
Пусть
дана система
 .
.
Сначала надо выделить неизвестные. Которые будут зависимыми(остальные будут независимыми); для этого надо, обведя нули, нарисовать «лесенку», иллюстрирующую ступенчатый вид матрицы. Под теми столбцами, где начинаются «ступеньки» этой «лесенки» подписать неизвестные, соответствующие этим столбцам, и рядом написать букву «з». В данном примере это будет выглядеть так:
 .
.

Выписанные неизвестные и будут считаться зависимыми.
Затем с помощью элементарных преобразований надо добиться, чтобы в столбцах соответствующих зависимым неизвестным, осталось лишь одно ненулевое число.
Делать это целесообразно двигаясь снизу вверх и справа на лево. В данном примере получим таким образом матрицу
 .
.
Теперь надо систему из матричной формы записи перевести в обычную форму:

Выражая в каждом уравнении зависимую неизвестную, получаем общее решение системы:

Теперь, придавая независимым неизменным произвольные значения и вычисляя зависимые, можно найти частное решение системы и сделать проверку.
В
этом примере положим
 =1,
=1, =2,
=2, =0,
тогда
=0,
тогда =-33,
=-33, =-7,
=-7, =
= ,
, =
= .
.
Проверка.
-33+8·1-4·(-7)-2· +4·
+4· -2·0=-33+8+28-1+2=4;
-2·0=-33+8+28-1+2=4;
2(-7)+7·2+4·
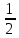 +2·
+2· -1·0=-14+14+2+1=3;
-1·0=-14+14+2+1=3; +3
·
+3
· =2 ; 2·
=2 ; 2· -3· 0=1.
-3· 0=1.
Замечание. Количество зависимых неизвестных должно равняться рангу матрицы.
Однородные линейные алгебраические системы
Определение 8. Однородные линейные алгебраические системы составлены из уравнений, у которых правые части раны нулю:

A
=
 –Матрица системы,
–Матрица системы,
Х
=
 – матрица-столбец неизвестных,
– матрица-столбец неизвестных,
Тогда матричная форма записи системы будет: АХ=0
Однородная
система всегда совместна, так как имеет
нулевое решение
 =0,
=0, =0,…,
=0,…, =0
или Х=0. Для существования ненулевого
решения однородной системы необходимо
и достаточно, чтобы ранг матрицы системы
был меньше числа неизвестных, т.е. чтобыr=r(A)
=0
или Х=0. Для существования ненулевого
решения однородной системы необходимо
и достаточно, чтобы ранг матрицы системы
был меньше числа неизвестных, т.е. чтобыr=r(A) n( приm=nэто
условие означает, чтоdetA=0).
n( приm=nэто
условие означает, чтоdetA=0).
Определение
9. ПустьQ -
множество всех решений однородной
системы. Всякий базис в множествеQсостоит изn-rвекторов
-
множество всех решений однородной
системы. Всякий базис в множествеQсостоит изn-rвекторов ,
, ,…,
,…, .Соответствующая
ему в каноническом базисе система
вектор-столбцов
.Соответствующая
ему в каноническом базисе система
вектор-столбцов ,
, ,
… ,
,
… , называетсяфундаментальной системой
решений.
называетсяфундаментальной системой
решений.
Общее решение однородной системы имеет вид:
Х= +
+ +…+
+…+ , где
, где ,
, ,…,
,…, –произвольные постоянные.
–произвольные постоянные.
Базисные
решения ,
, ,…,
,…, могут быть получены с помощью элементарных
преобразований матрицы системы
приведением ее к ступенчатому виду,
если независимым неизвестным придавать
поочередно значение 1, полагая остальные
равным нулю. Если задана неоднородная
система АХ=b, то ее общее
решение может быть найдено как сумма
общего решения соответствующей однородной
системы АХ=0 и произвольного частного
решения неоднородной системы.
могут быть получены с помощью элементарных
преобразований матрицы системы
приведением ее к ступенчатому виду,
если независимым неизвестным придавать
поочередно значение 1, полагая остальные
равным нулю. Если задана неоднородная
система АХ=b, то ее общее
решение может быть найдено как сумма
общего решения соответствующей однородной
системы АХ=0 и произвольного частного
решения неоднородной системы.
Пример 4. Найти фундаментальную систему решений однородной системы уравнений.

Решение.
 (2)-(1)
(3)-(1)
(2)-(1)
(3)-(1) (3)-2(2)
(3)-2(2) 2(1)
2(1)
 (1)+(2)
(1)+(2) .
.
 -з
-з
 -з
-з
 Общее
решение системы
Общее
решение системы
 Найдем
фундаментальную систему решений.
Найдем
фундаментальную систему решений.
Так как r(A)=2,n=4, то независимых неизвестных будетn-r=2 т.е. фундаментальная система будет состоять из двух векторов.
|
|
|
|
|
|
|
|
1 |
0 |
-
|
|
|
|
0 |
1 |
1 |
0 |
Таким
образом, =
= ,
, =
= -образуют
фундаментальную систему решений. Общее
решение системы есть Х=
-образуют
фундаментальную систему решений. Общее
решение системы есть Х= +
+ .
.
Ответ:
векторы ,
, образуют фундаментальную систему
решений, общее решение системы будет
Х=
образуют фундаментальную систему
решений, общее решение системы будет
Х= +
+ ,
,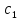 ,
, –произвольные постоянные,
–произвольные постоянные, =
= ,
, =
= .
.
Задания для самостоятельного решения.
Решить систему уравнений по формулам Крамера и матричным способом.
а)
 б)
б)
2. Решить систему уравнений по формулам Крамера и матричным способом.

3. Решить системы уравнений:
а) б)
б) в)
в)
Указание. Записать все три системы в виде одного матричного уравнения.
 ·
· =
= ,
т.е. в виде АХ=В, или Х=
,
т.е. в виде АХ=В, или Х= ·В.
·В.
Является система векторов линейно зависимой или нет?
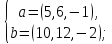 б)
б)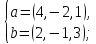 в)
в) г)
г)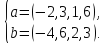
Проверить, что система векторов
 образует базис в
образует базис в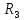 ,
и найти разложение вектораdв этом базисе, если:
,
и найти разложение вектораdв этом базисе, если:
а)
 ,
, ,
,
б) ,
, ,
,
в) ,
, ,
,
6. Найти методом Гаусса все решения системы

7. Исследовать систему уравнений с помощью теоремы Кронекера-Капелли.
 .
.
8. Исследовать системы уравнений с помощью теоремы Кронекера-Капелли и решить их.
а) ;
б)
;
б) ;
;
в) ;
г)
;
г) ;
;
д)
 .
.
9. Исследовать совместимость и найти общее решение следующих систем:
а)
 б)
б)
в)
г)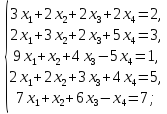 д)
д)
е) ж)
ж)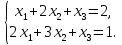
10. Найти фундаментальную систему решений и общее решение следующих систем:
а)

б)
в) г)
г)
д)
11. Найти общие решения неоднородных систем, используя фундаментальную систему решений соответствующих однородных:
а)
б)
Векторная алгебра