
- •§ 1. Уравнение неразрывности
- •§ 2. Уравнения движения и равновесия
- •Уравнением моментов
- •§ 3. Уравнения состояния (математические модели)
- •§ 4. Уравнения состояния гидромеханики
- •§ 5. Основные уравнения теории фильтрации
- •§ 5.1 Линейные уравнения и граничные задачи фильтрации.
- •§ 6. Мгновенные уравнения состояния и критерии прочности
- •§ 7. Временные уравнения состояния и критерии длительной прочности
- •§ 8. Общая система уравнений механики деформируемого твердого тела
§ 3. Уравнения состояния (математические модели)
Уравнения неразрывности и движения (2.3) и (2.9), справедливые при непрерывных движениях любой сплошной среды, недостаточны для описания поведения конкретной среды, так как их число меньше числа входящих в них неизвестных (перемещения, деформации, скорости, напряжения и др.). Это понятно и с другой точки зрения. Различные реальные тела при одних и тех же внешних условиях ведут себя по-разному, что никак не отражено в общих уравнениях (2.3) и (2.9). Поэтому говорят, что такая система уравнений не замкнута. Построить замкнутую систему уравнений — значит построить математическую модель изучаемой сплошной среды. Для этого к имеющимся уравнениям необходимо присоединить так называемые механические уравнения состояния, которые выражают связь между кинематическими и динамическими величинами.
Механические свойства реальных тел довольно сложны, и поэтому уравнения состояния устанавливаются на основании опытных данных. В настоящее время для многих тел установлены определенные механические свойства и соответствующие им уравнения состояния.
В силу характерных особенностей различают математические модели твердых деформируемых тел, жидкостей и газов, хотя такое деление в определенном смысле условно.
С позиций механики сплошной среды твердые тела, жидкости и газы различаются по действию, оказываемому на них внешними силами, именно по неодинаковой сопротивляемости изменению формы. Газы практически не сопротивляются изменению формы, капельные жидкости сопротивляются изменению формы значительно слабее, чем твердые тела. Кроме того, они различаются по характеру и степени проявления упругих, вязких и пластических свойств, их влиянию на изучаемый процесс.
Все это находит отражение в уравнениях состояния, т. е. в зависимостях между компонентами тензоров напряжений σij и деформаций εij (или скорости деформаций ξij) или компонентами девиаторов напряжений sij и деформации eij (или скорости деформаций λij). По существу эти уравнения являются классификатором разделов механики сплошной среды.
При формулировке инженерных задач не следует стремиться к использованию уравнений состояния, описывающих все детали механического поведения тела под воздействием внешних сил. Наоборот, целесообразно выбрать простейшую математическую модель, которая отражала бы лишь самые существенные свойства. В противном случае решить задачу будет либо чрезвычайно сложно, либо вовсе невозможно.
Приведем наиболее известные уравнения состояния, используемые в гидромеханике и механике твердого деформируемого тела.
Следует обратить внимание, что структурное сходство этих моделей придает общность исходным уравнениям механики сплошной среды, несмотря на существенное различие в физическом поведении разных тел.
§ 4. Уравнения состояния гидромеханики
1. Модель идеальной жидкости – это простейшая механическая модель сплошной среды, для которой характерно отсутствие сопротивления (сил трения) при скольжении одного слоя жидкости по другому, отдельные части взаимодействуют только в виде нормального давления, т. е. в любой точке идеальной жидкости касательные напряжения
EMBED
Equation.3
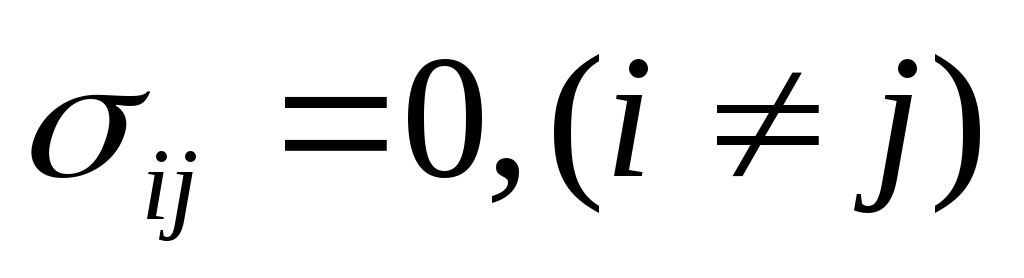 ,
,
а нормальные напряжения
EMBED
Equation.3
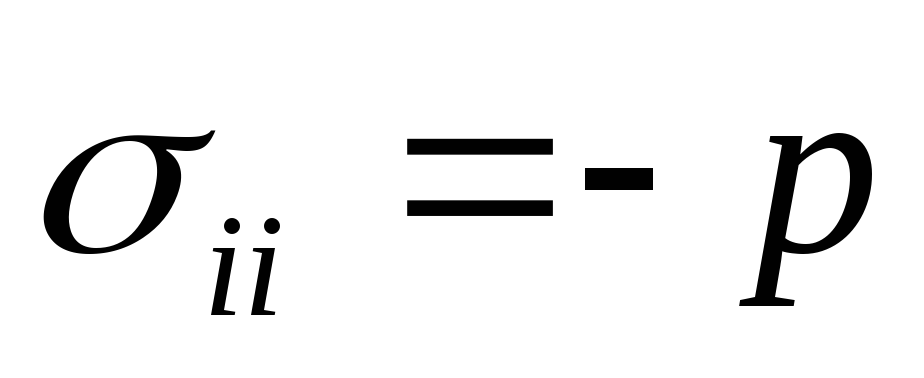 ,
,
или через компоненты девиатора напряжений
EMBED
Equation.3
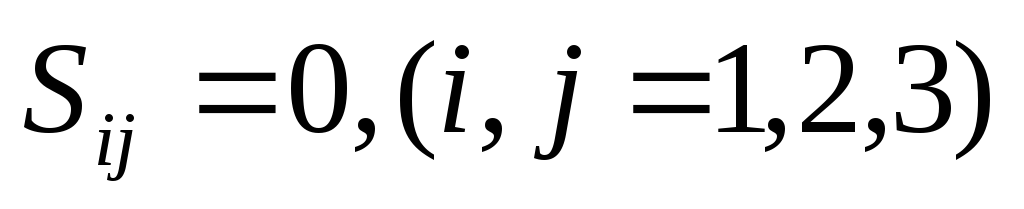 .
.
Уравнением состояния для этой жидкости служит зависимость плотности ρ от давления р и температуры Т:
EMBED
Equation.3
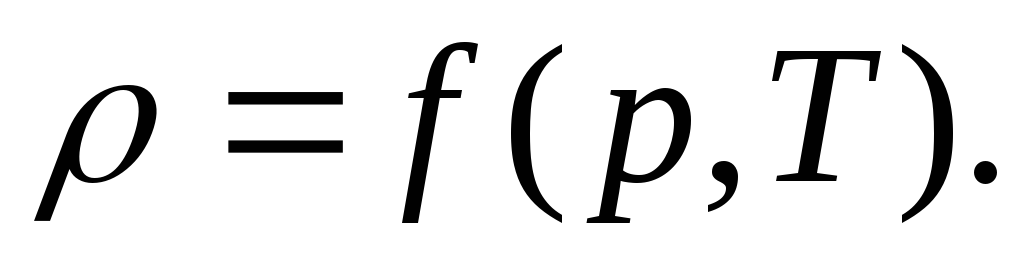 (2.11)
(2.11)
Для идеального газа приемлемо уравнение Клапейрона — Менделеева
EMBED
Equation.3
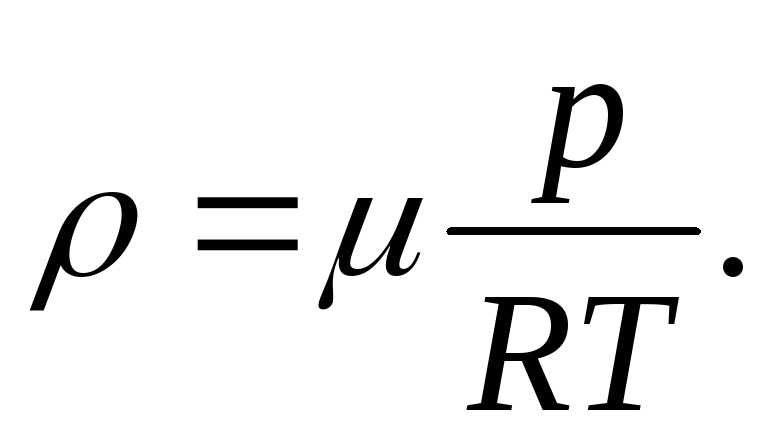
Если
плотность жидкости — функция только
давления
EMBED Equation.3
![]() ,
то
жидкость называют баротропной.
,
то
жидкость называют баротропной.
Когда имеет место степенная зависимость ( с и n -постоянные), то говорят, что движение происходит при политропическом процессе.
EMBED
Equation.3
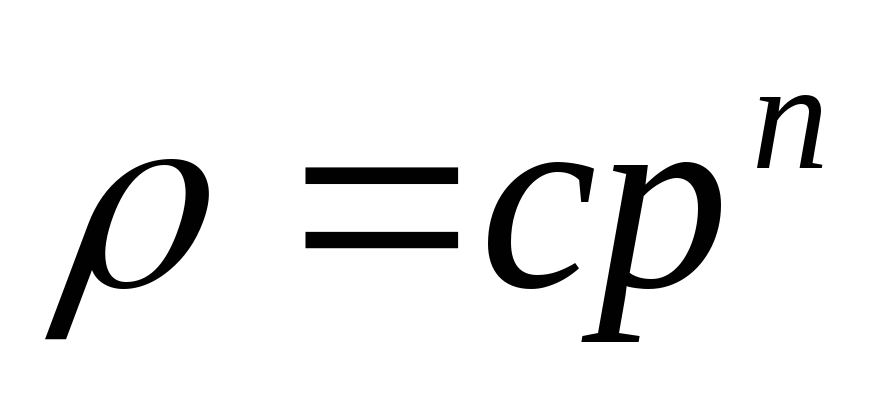
Для капельных жидкостей сжимаемость чрезвычайно мала, и в большом диапазоне изменения давления принимается линейная зависимость
EMBED
Equation.3
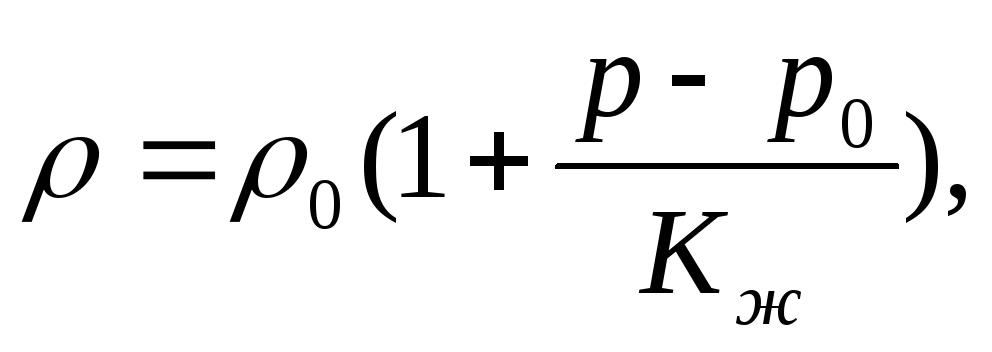
где ρ0 - плотность, соответствующая давлению р0; Кж - модуль объемного сжатия.
Порядок модуля объемного сжатия жидкостей равен 104 n МПа.
Экспериментальные данные и общие физические соображения показывают, что любая среда при очень больших температурах и давлениях практически обладает свойствами идеальной жидкости.
В нормальных условиях модель идеальной жидкости широко используется при изучении движения многих жидкостей и газов вдали от твердых границ.
Одно из наиболее известных уравнений движения идеальной жидкости — закон Бернулли
EMBED
Equation.3
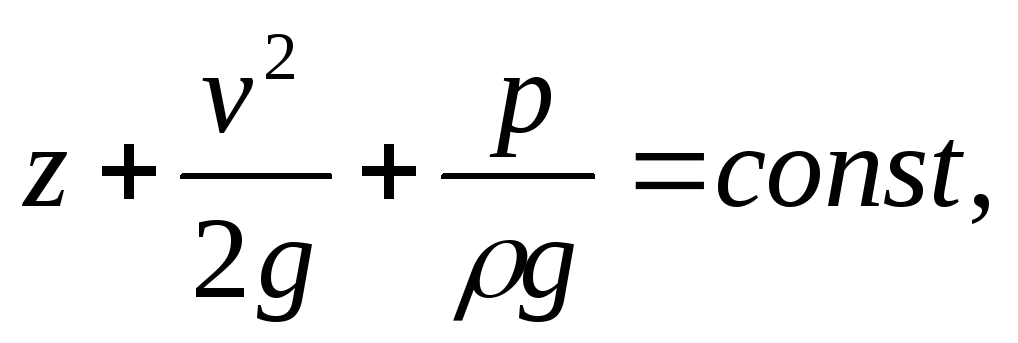
который гласит, что при установившемся движении несжимаемой идеальной жидкости сумма геометрической (z), скоростной (v2/2g) и пьезометрической (p/ρg) высот вдоль линии тока остается величиной постоянной.
Отметим тот факт, что Пуазейль был по профессии медиком и интересовался прохождением крови через малые кровеносные сосуды. Сейчас известно, что кровь не является ньютоновской жидкостью, поэтому автор опыта, экспериментально подтвердившего на примере воды предположения Ньютона, в каком-то смысле является первым исследователем неньютоновских сред.
Ввиду того, что в размерность v входят только метры и секунды (и не входит размерность массы), эту величину называют кинематический коэффициентом вязкости (или кинематической вязкостью). Размерность см2/с называется стокс (в честь английского гидромеханика Дж. Стокса. который сформулировал дифференциальные уравнения движения вязкой жидкости), и обозначается Ст:
1Ст=10-4 м2/с.
Иногда
в качестве единицы EMBED Equation.3
![]() используют г/см-с, которая называется
пуаз (в честь французского врача А.
Пуазейля, выполнившего фундаментальные
исследования движения вязкой жидкости)
и обозначается П.
используют г/см-с, которая называется
пуаз (в честь французского врача А.
Пуазейля, выполнившего фундаментальные
исследования движения вязкой жидкости)
и обозначается П.
Па∙с = 10∙П.
2. Модель - вязкой ньютоновской жидкости - следующая по сложности, которую используют, когда силами трения или напряжениями сдвиги при движении жидкости пренебречь нельзя, Уравнениями состояния для такой жидкости, кроме уравнения вида (2.11), будет
EMBED
Equation.3
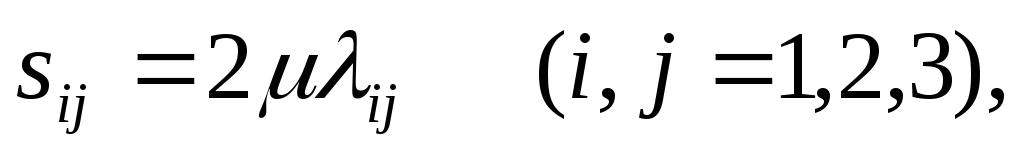 (2.12)
(2.12)
т.е. прямо пропорциональная зависимость между компонентами девиатора напряжений и скоростей деформаций. Учитывая динамические величины и элементы теории напряжений, имеем равносильные уравнения, выраженные через компоненты тензоров напряжений и скоростей деформаций:
EMBED
Equation.3
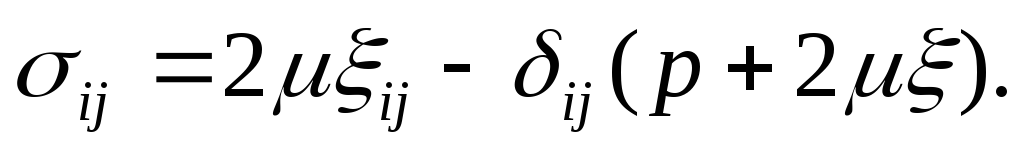
При плоском слоистом течении жидкости вдоль оси Оx1, когда v1 =v1(x1, х2), v2 = v3 = 0, нормальные и касательные напряжения равны:
EMBED
Equation.3
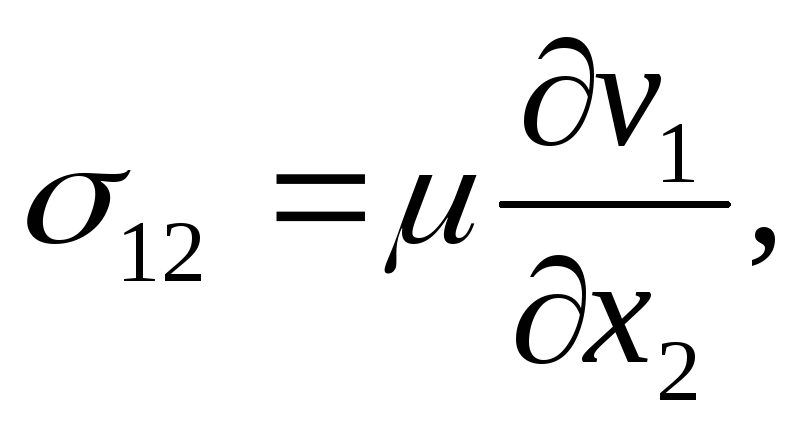 EMBED Equation.3
EMBED Equation.3
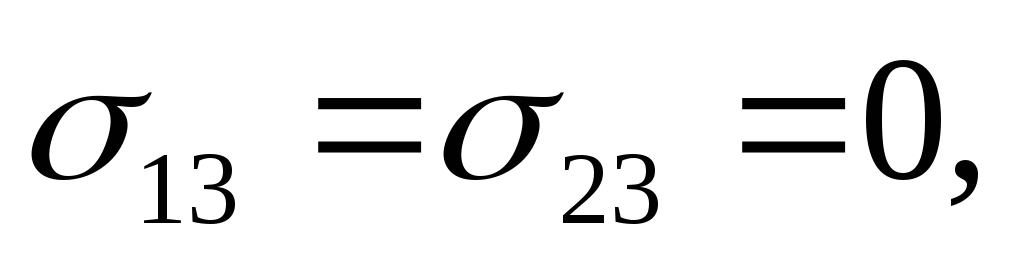
EMBED
Equation.3
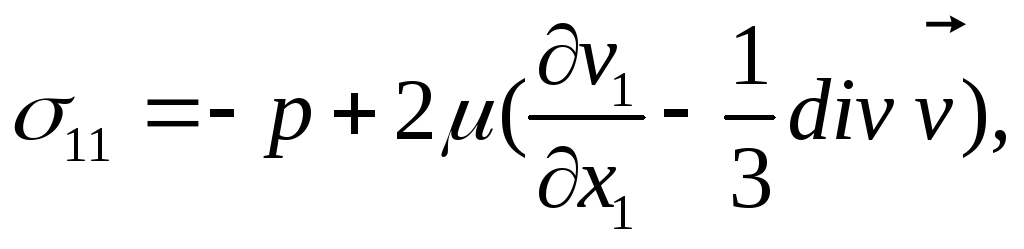
EMBED
Equation.3

Если,
кроме того, жидкость несжимаемая EMBED
Equation.3
![]() и скорость
v1
не
зависит от х1,
то
уравнение состояния имеет простейший
вид
и скорость
v1
не
зависит от х1,
то
уравнение состояния имеет простейший
вид
EMBED
Equation.3
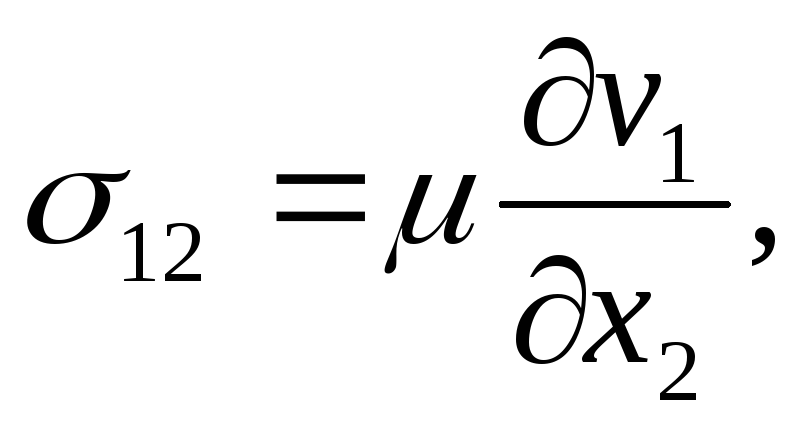 EMBED
Equation.3
EMBED
Equation.3
![]() EMBED
Equation.3
EMBED
Equation.3
![]()
Коэффициент пропорциональности μ называется коэффициентом вязкости или динамической вязкостью жидкости. Размерность этого коэффициента, согласно соотношениям (2.12), Динамическая вязкость воды при 20° С равна 10-3 Па·с.
Иногда пользуются отношением μ/ρ, которое называется кинематической вязкостью и обозначается буквой υ. Размерность этой величины м2/с.
Для газов и капельных жидкостей динамическая и кинематическая вязкости слабо зависят от давления, но сильно от температуры. Как видно из данных, приведенных ниже, оба коэффициента вязкости воды убывают с повышением температуры, а коэффициенты вязкости воздуха возрастают. Эта закономерность свойственна всем жидкостям и газам.
|
Т О С |
0 |
20 |
40 |
60 |
80 |
100 |
|
вода | ||||||
|
103µ, Па∙с |
1,792 |
1,005 |
0,656 |
0,469 |
0,357 |
0,284 |
|
106ν, м/с |
1,792 |
1,007 |
0,661 |
0,477 |
0,367 |
0,296 |
|
воздух | ||||||
|
105µ, Па∙с |
1,709 |
1,808 |
1,904 |
1,997 |
2,088 |
2,175 |
|
104ν, м/с |
0,132 |
0,15 |
0,169 |
0,188 |
0,209 |
0,23 |
Применяются различные эмпирические формулы зависимости вязкости газов и жидкостей от температуры, но из-за их сложности и малой общности предпочтительно пользоваться таблицами.
Свойствами ньютоновских жидкостей, описываемых уравнениями (2.12), обладает большинство чистых жидкостей и газов. Однако многие растворы, в том числе буровые и тампонажные, проявляют свойства, отличные от свойств ньютоновских жидкостей. Вязкость таких неньютоновских жидкостей зависит не только от температуры и давления, но и от скорости сдвига, деформации, времени, характера движения.
3. Модель неньютоновского поведения жидкостей.
Их основной признак заключается в нелинейной зависимости между компонентами девиаторов напряжений и скоростей деформаций.
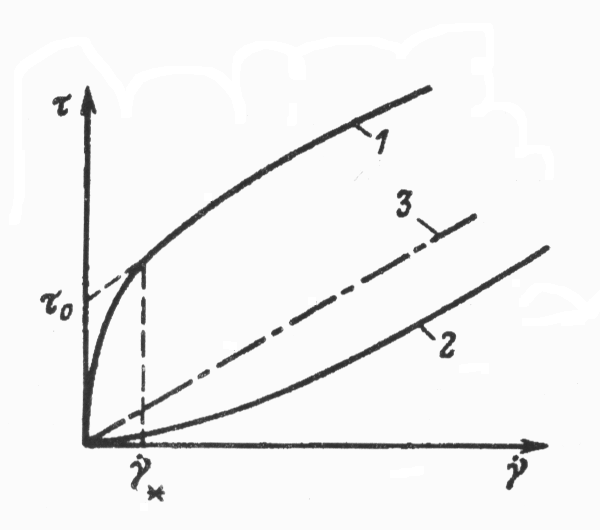
Рис 2.1 Характерные зависимости напряжения сдвига от скорости деформации сдвига:
1 – псевдопластичная жидкость;
2 – дилатантная жидкость;
3 – ньютоновская жидкость.
На
рис 2.1 показаны две характерные кривые
зависимости напряжения
сдвига EMBED Equation.3
![]() от скорости деформации сдвига
EMBED Equation.3
от скорости деформации сдвига
EMBED Equation.3
![]() для неньютоновских жидкостей при плоском
прямолинейном
установившемся движении вдоль оси Ох1.
Здесь
же для сопоставления
штрихпунктиром показана линейная
зависимость для
ньютоновской жидкости.
для неньютоновских жидкостей при плоском
прямолинейном
установившемся движении вдоль оси Ох1.
Здесь
же для сопоставления
штрихпунктиром показана линейная
зависимость для
ньютоновской жидкости.
Поведение жидкости, описываемое кривой 1, называется псевдопластичным, а кривой 2 — дилатантным. Предлагалось много различных вариантов аппроксимации этих кривых. Но наиболее широкое применение получили двухпараметрические аппроксимации:
а) модель Шведова — Бингама
EMBED
Equation.3
 (2.13)
(2.13)
используемая для псевдопластичных жидкостей;
б) модель Освальда — Вейля, или степенная модель,
EMBED
Equation.3
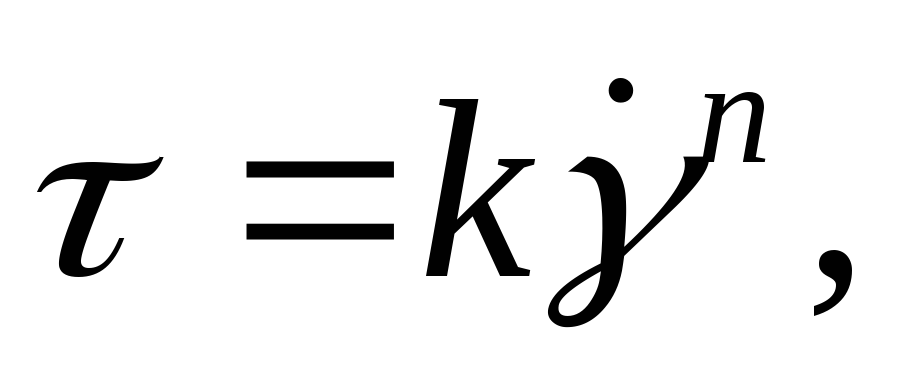 (2.14)
(2.14)
используемая для обоих типов жидкостей, где τ0 — предельное (или динамическое) напряжение сдвига; η — пластическая (или структурная) вязкость; k — показатель консистенции; п — показатель неньютоновского поведения: при п < 1 жидкость псевдопластичная, при п>1 — дилатантная.
Между параметрами моделей (2.13) и (2.14) легко устанавливается следующая связь:
EMBED
Equation.3
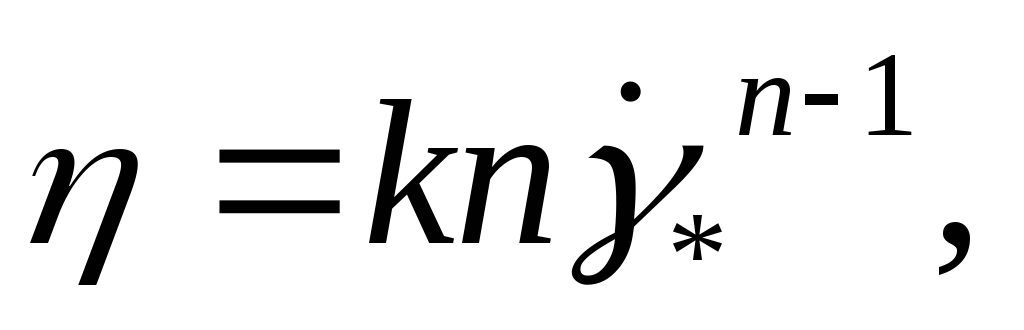 EMBED Equation.3
EMBED Equation.3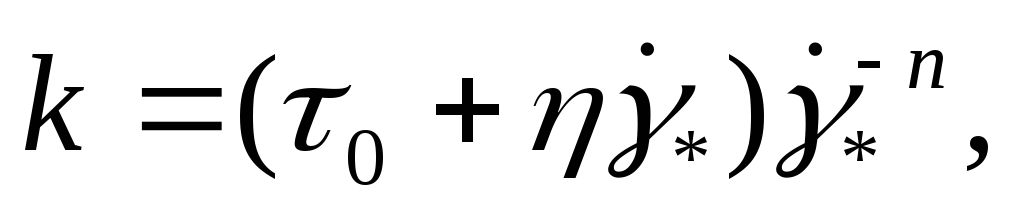
EMBED
Equation.3
 EMBED Equation.3
EMBED Equation.3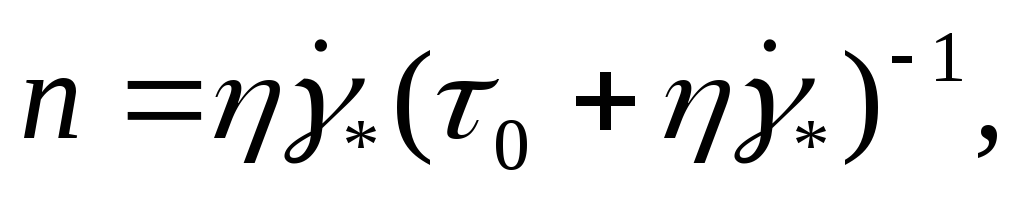
где
EMBED Equation.3
![]() —
скорость деформации сдвига, выше которой
зависимость
EMBED Equation.3
—
скорость деформации сдвига, выше которой
зависимость
EMBED Equation.3
![]() от
EMBED Equation.3
от
EMBED Equation.3
![]() практически линейная (см. рис. 10).
практически линейная (см. рис. 10).
Так
как в системе единиц СИ размерность
величин [
EMBED Equation.3
![]() ]
= Па, [η]
= Па·с, и [
EMBED Equation.3
]
= Па, [η]
= Па·с, и [
EMBED Equation.3
![]() ]
= с-1,
то
размерность параметра [k]
= Па·с.
]
= с-1,
то
размерность параметра [k]
= Па·с.
Среда, для которой справедливо уравнение (2.13), называется вязкопластичной бингамовской жидкостью. Она характеризуется тем, что обладает пространственной жесткой структурой и благодаря этому сопротивляется внешнему воздействию до тех пор, пока вызванное им напряжение сдвига не превзойдет предельного значения, соответствующего этой структуре. После этого структура полностью разрушается и жидкость начинает вести себя как обычная ньютоновская вязкая жидкость при кажущемся напряжении, равном избытку действительного напряжения τ над предельным τ0. При уменьшении этого кажущегося напряжения до нуля пространственная жесткая структура восстанавливается.
Необходимо
подчеркнуть, что реологические параметры
η, τ0
и k,
п
для
бурового и тампонажного растворов
зависят от температуры,
давления, состава и диапазона изменения
скорости деформации
сдвига
EMBED Equation.3
![]() ,
для которой справедливы модели (2.13) и
(2.14).
,
для которой справедливы модели (2.13) и
(2.14).
4. Модель неньютоновских несжимаемых вязкопластичных жидкостей при ламинарном (структурном) режиме течения. Чтобы установить характер зависимости между касательными напряжениями и скоростями деформации сдвига и определить реологические параметры жидкости в заданных условиях, используют наиболее простые формы движения: установившееся ламинарное (слоистое) течение жидкости вдоль оси цилиндрической трубы или тангенциальное течение между двумя соосными цилиндрами, т. е. течения, при которых линии тока — прямые линии или концентрические окружности. Подобные течения реализуются в специальных приборах, называемых капиллярными и ротационными вискозиметрами соответственно.
При
течении жидкости в трубке радиуса R
задают
объемный расход
Q
и измеряют разность давлений Δр
в
двух точках потока, расположенных
вдали от концов трубки на расстоянии L
друг
от друга.
В координатах средней скорости деформации
сдвига EMBED Equation.3
![]() и касательного напряжения у поверхности
трубки EMBED Equation.3
и касательного напряжения у поверхности
трубки EMBED Equation.3![]() строится график.
строится график.
Этот
график в общем случае необходимо
перестроить в координатах локальной
скорости деформации
сдвига
EMBED Equation.3
![]() и
напряжения τ,
используя для этого
уравнение :
и
напряжения τ,
используя для этого
уравнение :
EMBED
Equation.3
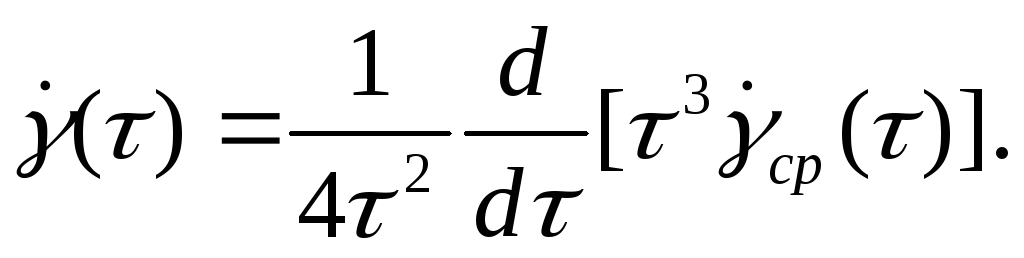
Однако
легко показать, что для вязких и
вязкопластичных жидкостей, описываемых
уравнениями (2.13) или (2.14), перестраивать
график
EMBED Equation.3
![]() ~
τ в
EMBED Equation.3
~
τ в
EMBED Equation.3
![]() ~
τ
нет
необходимости, достаточно только
реологические
параметры τ0
и
~
τ
нет
необходимости, достаточно только
реологические
параметры τ0
и
EMBED
Equation.3
![]() - длямодели
Шведова — Бингама и
- длямодели
Шведова — Бингама и
EMBED
Equation.3
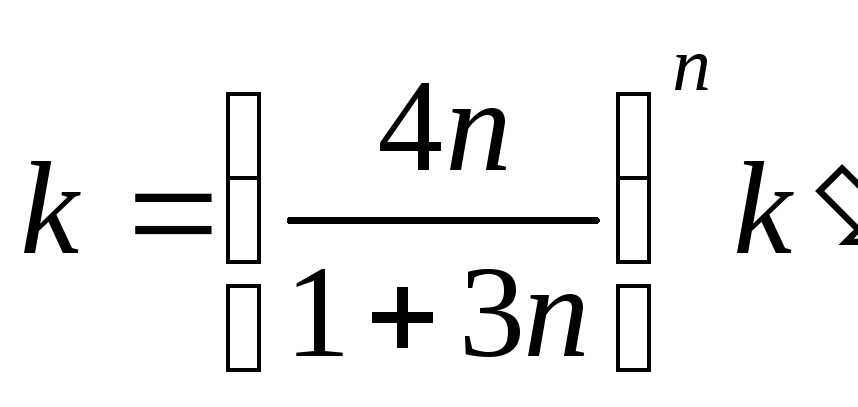 —
в степенной модели, где
EMBED Equation.3
—
в степенной модели, где
EMBED Equation.3
![]() и
EMBED Equation.3
и
EMBED Equation.3
![]() —
параметры, определенные зависимостью
EMBED Equation.3
—
параметры, определенные зависимостью
EMBED Equation.3
![]() от τ.
от τ.
При течении жидкости между двумя вертикальными соосными цилиндрами длиной L, из которых наружный вращается с угловой скоростью ω, реологические параметры для бингамовской жидкости (2.13) могут быть определены из соотношения
EMBED
Equation.3
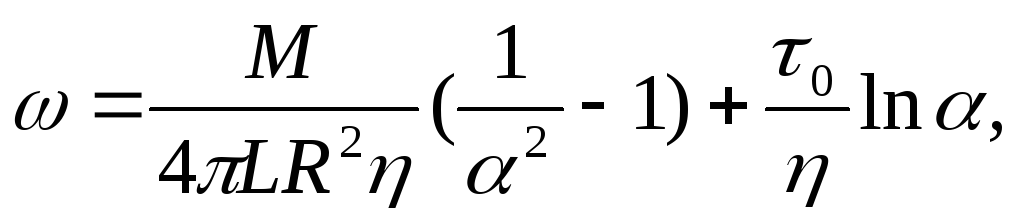
а для жидкости, соответствующей степенной модели (2.14), из формулы
EMBED
Equation.3
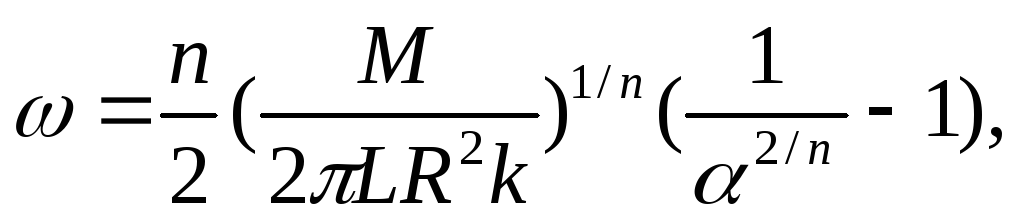
где М – вращающий момент, приложенный к наружному цилиндру; α = R0/R; R0 , R - радиусы внутреннего и внешнего цилиндров соответственно.
Для
производственного течения несжимаемых
EMBED Equation.3
![]() вязкопластичных жидкостей используются
следующие уравнения состояния, обобщающие
уравнения (2.12) и модели (2.13), (2.14):
вязкопластичных жидкостей используются
следующие уравнения состояния, обобщающие
уравнения (2.12) и модели (2.13), (2.14):
EMBED
Equation.3
![]() при EMBED Equation.3
при EMBED Equation.3![]()
EMBED
Equation.3
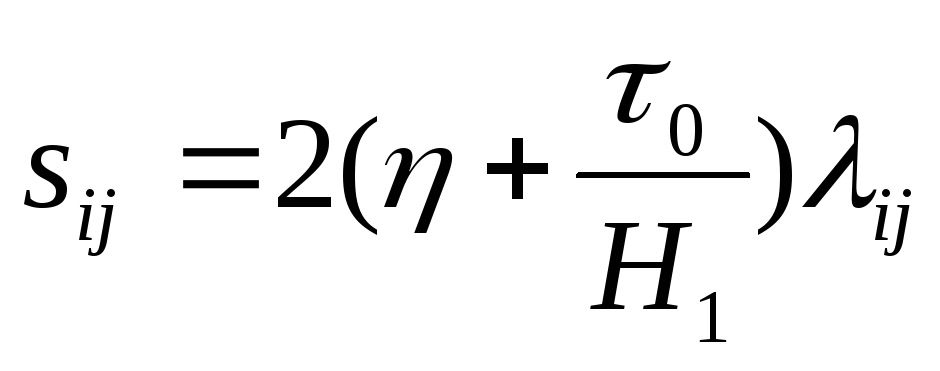 при EMBED Equation.3
при EMBED Equation.3![]() (2.15)
(2.15)
и
EMBED Equation.3
![]() (2.16)
(2.16)
где
H1,
Т
— интенсивность
скоростей деформации сдвига при EMBED
Equation.3
![]() и интенсивность касательных напряжений.
и интенсивность касательных напряжений.
При определенных нестационарных режимах течения буровые и тампонажные растворы могут проявлять дополнительные свойства неньютоновского поведения:
тиксотропность — зависимость жесткости структуры от продолжительности деформирования и предыстории движения;
запаздывание во времени установления деформации при действии постоянного напряжения или, наоборот, запаздывание во времени установления напряжений при постоянной деформации (релаксация напряжений) и т. д.
Количественное изучение этих и других важных свойств до настоящего времени остается в значительной степени неразработанным разделом механики жидкостей вообще, а для буровых и тампонажных растворов не выходит за пределы отдельных опытных иллюстраций.
Тот факт, что вязкие или вязкопластичные свойства, а следовательно уравнения состояния (2.15), (2.16), будут определяющими лишь при ламинарном (или структурном) режиме течения, т. е. тогда траектории частиц жидкости имеют вполне определенное, упорядоченное (регулярное) направление, - наиболее существенная особенность движения любой жидкости.
5. Модель неньютоновских вязкопластичных жидкостей при турбулентном режиме течения - неупорядоченном (нерегулярном), хаотическом движении. Опыты показывают, что по мере увеличения скорости течения всякое упорядоченное движение частиц жидкости постепенно нарушается и переходит в новую форму — турбулентное движение, при котором движение частиц становится неупорядоченным (нерегулярным), хаотическим.
Процессы возникновения и развития такого движения носят случайный характер и не поддаются строгому теоретическому анализу, требуя для своего изучения своеобразных статистических методов.
До настоящего времени нет ясного представления, как ламинарное движение вязкой жидкости становится турбулентным, несмотря на то, что первые научные наблюдения турбулентных движений были выполнены сто двадцать восемь лет тому назад!!! Еще сложнее проблема разрушения структурного режима течения буровых и тампонажных растворов и переход его в развитое турбулентное движение. Английский физик О. Рейнольдс, изучая движение воды цилиндрической трубе, в 1883 г. впервые обнаружил, что переход ламинарного движения в турбулентное наступает при достижении критического значения некоторого безразмерного параметра
EMBED
Equation.3
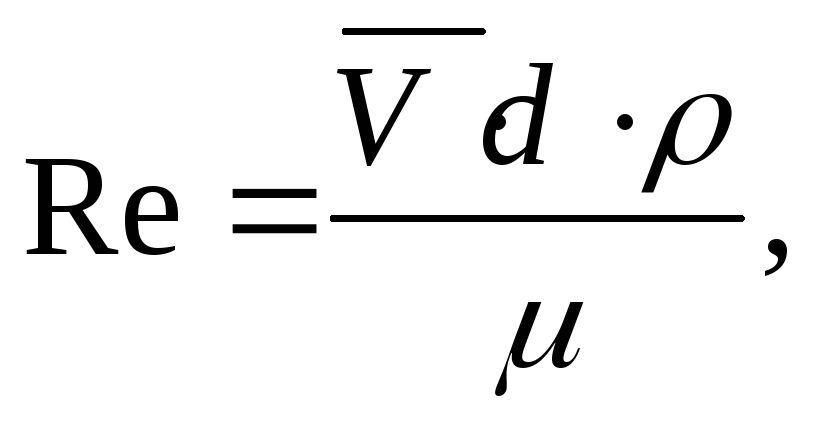 (2.17)
(2.17)
где
EMBED Equation.3
![]() - средняя скорость потока;d
— диаметр трубы;
EMBED Equation.3
- средняя скорость потока;d
— диаметр трубы;
EMBED Equation.3
![]() —
соответственно
плотность и вязкость жидкости.
—
соответственно
плотность и вязкость жидкости.
По опытным данным О. Рейнольдса, нижняя граница критического числа Reкр составила 2000, а верхняя — 13000. В последующем более тщательными опытами было установлено, что для ньютоновских жидкостей наиболее вероятная нижняя граница равна 2320, а верхнюю можно довести до 50000. Оказалось, что запаздывание ламинарного течения связано с удалением возмущений на входе в трубу. Чем плавнее вход в трубу, тем позже наступает турбулентный режим.
Опытами было установлено также, что на величину верхней границы Reкр сильное влияние оказывают отклонение трубы от цилиндрической формы, заметная шероховатость поверхности трубы, наличие в жидкости твердых тел, коллоидных или дисперсных образований, изменение граничных условий, действие внешних возмущений и другие факторы.
Для вязкопластичных сред переход от структурного режима течения к турбулентному принято определять с помощью обобщенного параметра Рейнольдса:
для степенной модели
EMBED
Equation.3
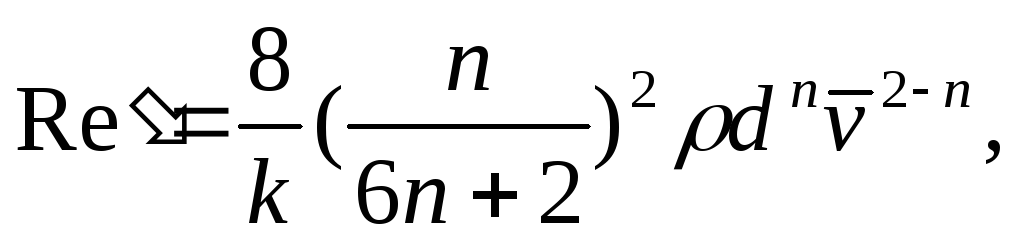 (2.18)
(2.18)
для модели Шведова — Бингама
EMBED
Equation.3
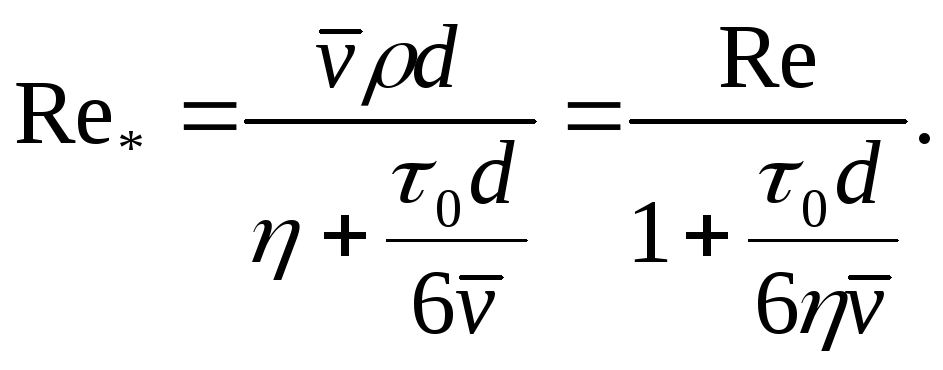 (2.19)
(2.19)
Нижняя граница критических значений обобщенных параметров Rе', Rе* равна 2100.
Наряду с изучением переходных процессов в цилиндрических трубах были изучены движение жидкостей в пространстве между соосными цилиндрами в осевом и тангенциальном направлениях и при обтекании твердых тел набегающим потоком жидкости, а также обнаружено качественное сходство переходных процессов, определяемых по тем же параметрам Рейнольдса (2.18) и (2.19), где под d следует понимать характерное сечение потока или линейный размер тел.
Изучение переходных режимов и практическое определение Rе базируются главным образом на установлении опытной зависимости коэффициента гидравлического сопротивления от параметра Рейнольдса, соответствующего данной реологической модели.
Отличительным
признаком турбулентных течений является
зависимость
скорости от времени в любой точке потока.
Для количественного
описания турбулентных течений О.
Рейнольдc
предложил
действительные скорости потока vi
(i
=
1,
2,
3) в данной точке представлять в виде
суммы средних во времени скоростей
EMBED Equation.3
![]() и
пульсационных скоростей (пульсаций)
EMBED Equation.3
и
пульсационных скоростей (пульсаций)
EMBED Equation.3
![]() ,
т.
е.
EMBED Equation.3
,
т.
е.
EMBED Equation.3
![]() .
Аналогично
представляется и давление EMBED Equation.3
.
Аналогично
представляется и давление EMBED Equation.3
![]() .
Форма
уравнений движения и неразрывности
сохраняется.
В этом случае следует только заменить
скорости vi
и давление
р
средними
скоростями
EMBED Equation.3
.
Форма
уравнений движения и неразрывности
сохраняется.
В этом случае следует только заменить
скорости vi
и давление
р
средними
скоростями
EMBED Equation.3
![]() и давлениями
EMBED Equation.3
и давлениями
EMBED Equation.3
![]() ,
а
вместо напряжений
EMBED Equation.3
,
а
вместо напряжений
EMBED Equation.3
![]() использовать сумму
использовать сумму
EMBED
Equation.3
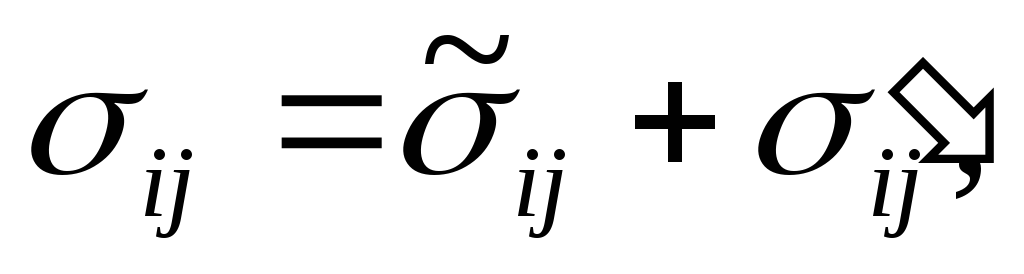
где
EMBED Equation.3
![]() — компоненты напряжений, связанные со
средними скоростями
уравнениями состояния (2.12), (2.15) или
(2.16); EMBED Equation.3
— компоненты напряжений, связанные со
средними скоростями
уравнениями состояния (2.12), (2.15) или
(2.16); EMBED Equation.3
![]() — дополнительные
компоненты напряжений, возникающие
вследствие пульсаций,
они называются напряжениями
Рейнольдса.
— дополнительные
компоненты напряжений, возникающие
вследствие пульсаций,
они называются напряжениями
Рейнольдса.
Иначе
говоря, доказана возможность применения
основных уравнений
движения механики сплошной среды для
решения задач турбулентного
течения при условии, что величины vi,
р
и
EMBED Equation.3
![]() ,
входящие
в эти уравнения, заменены соответственно
на величины
EMBED Equation.3
,
входящие
в эти уравнения, заменены соответственно
на величины
EMBED Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() и
EMBED
Equation.3
и
EMBED
Equation.3
![]() .
.
Предложено
несколько полуэмпирических уравнений
состояния для напряжений
Рейнольдса
EMBED Equation.3
![]() .
Наиболее
известно и широко используется
уравнение Прандтля:
.
Наиболее
известно и широко используется
уравнение Прандтля:
EMBED
Equation.3
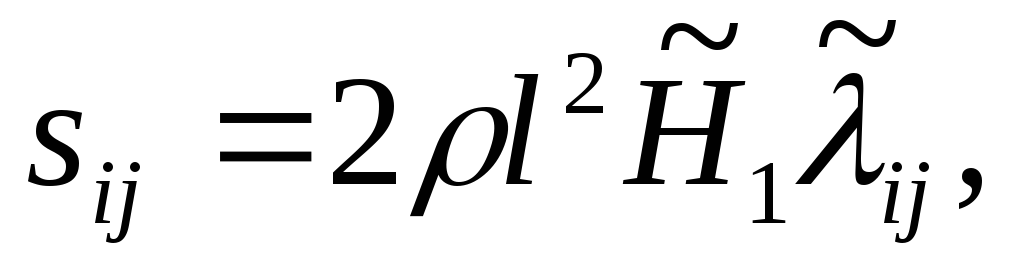 (2.20)
(2.20)
где l —коэффициент, характеризующий геометрическую структуру турбулентного потока, называемый путем смешения (перемешивания) или масштабом турбулентности, зависящий от расстояния до стенки канала.
В частном случае при течении жидкости между параллельными плоскостями в направлении оси Ох1 уравнение (2.20) принимает вид
EMBED
Equation.3
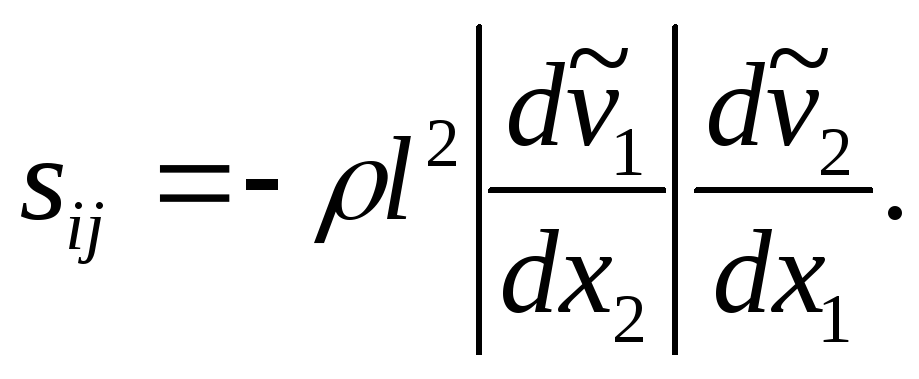
Прандтль, анализируя свойства турбулентного потока в трубах вблизи твердой стенки, принимал l = 0,36s, где s — расстояние от стенки трубы.
6.
Модель
неньютоновских
многокомпонентных
смесей
вязкопластичных жидкостей
при
любых
режимах
течения.
Таким
образом, общая задача гидромеханики в
определении компонент
vi
(i
=
1,
2,
3)
вектора скорости EMBED Equation.3
![]() ,
компонент
симметричного девиатора
напряжений sij
=sji
(i,
j=1,
2, 3), давления р
и
плотности ρ жидкости в любой точке
области.
,
компонент
симметричного девиатора
напряжений sij
=sji
(i,
j=1,
2, 3), давления р
и
плотности ρ жидкости в любой точке
области.
В общем случае эти одиннадцать искомых функций должны в ламинарном режиме течения удовлетворять следующей системе дифференциальных уравнений:
движения
EMBED
Equation.3
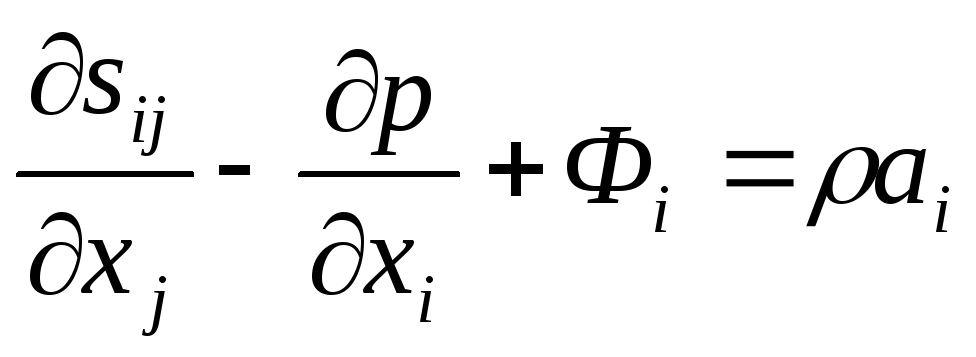 (i=1,
2, 3); (2.21)
(i=1,
2, 3); (2.21)
неразрывности движения или сохранения массы
EMBED
Equation.3
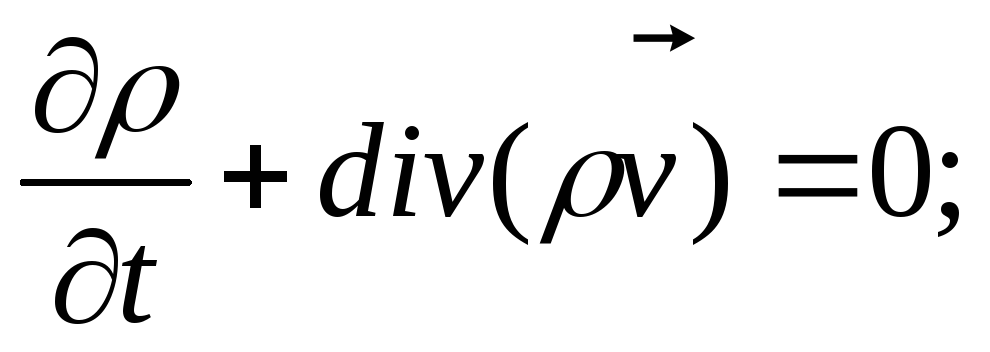 (2.22)
(2.22)
и механического состояния
s = f(p); (2.23)
EMBED
Equation.3
 (2.24)
(2.24)
Подставляя в уравнения (2.21) соотношения (2.24)можно получить уравнения Навье — Стокса, Генки — Ильюшина и др.
При
турбулентных течениях жидкостей и
газов, согласно сказанному
выше, система уравнений (2.21) — (2.24)
сохраняет свой вид,
но под величинами
vi,
EMBED Equation.3
![]() ,
р
необходимо
понимать усредненные
по времени значения
EMBED Equation.3
,
р
необходимо
понимать усредненные
по времени значения
EMBED Equation.3
![]() ,
EMBED
Equation.3
,
EMBED
Equation.3
![]() ,
EMBED Equation.3
,
EMBED Equation.3
![]() ,
где
напряжения Рейнольдса
EMBED Equation.3
,
где
напряжения Рейнольдса
EMBED Equation.3
![]() связаны
с компонентами средних скоростей
деформаций EMBED Equation.3
связаны
с компонентами средних скоростей
деформаций EMBED Equation.3
![]() ,
например, уравнением Прандтля (2.20).
,
например, уравнением Прандтля (2.20).
Для удобства выпишем обозначения основных величин:
EMBED
Equation.3
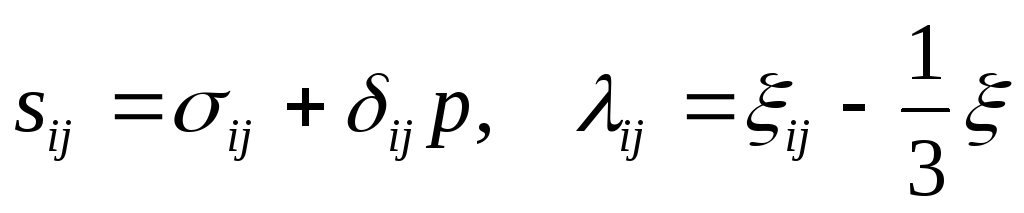 -
компоненты девиаторов напряжений и
скоростей деформаций соответственно;
-
компоненты девиаторов напряжений и
скоростей деформаций соответственно;
EMBED
Equation.3
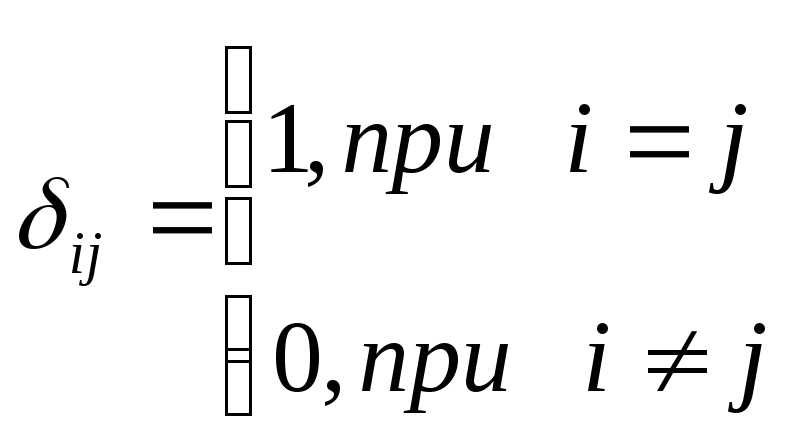 -
символ Кронекера;
-
символ Кронекера;
EMBED
Equation.3
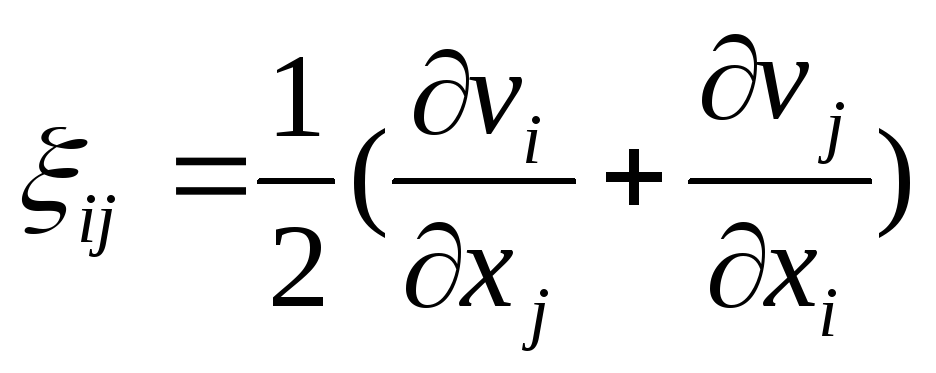 —
соотношения Коши; (2.25)
—
соотношения Коши; (2.25)
EMBED
Equation.3
![]() — скорость деформации объема;
— скорость деформации объема;
EMBED
Equation.3
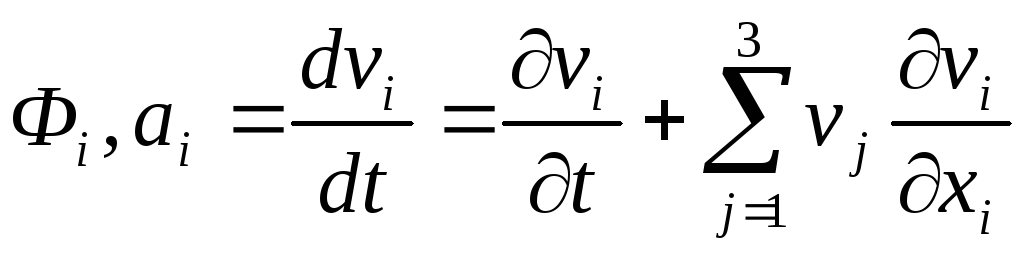 — проекции объемных сил и ускорении;
— проекции объемных сил и ускорении;
EMBED
Equation.3
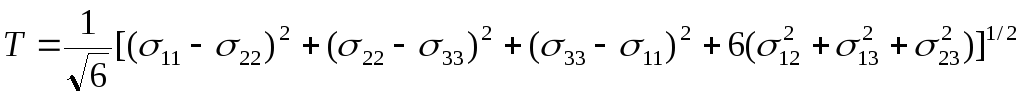 -
(2.26)
-
(2.26)
интенсивность касательных напряжении;
EMBED
Equation.3
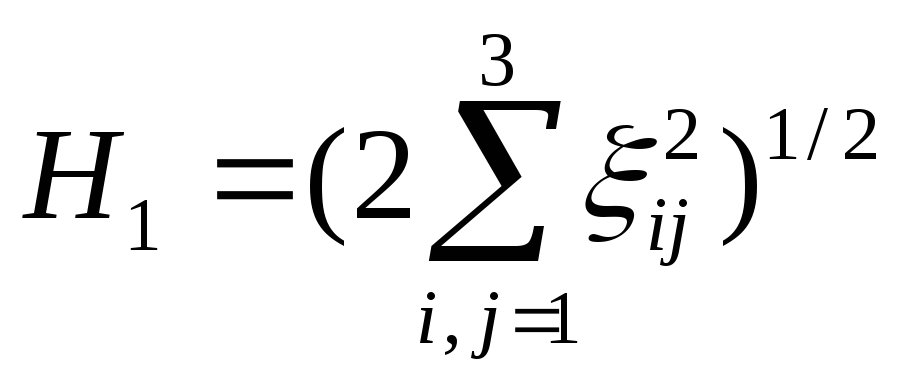 -
(2.27)
-
(2.27)
интенсивность скорости деформации сдвига при ξ=0.
Единственность и однозначность решения системы дифференциальных уравнений (2.21) - (2.24) возможны лишь при выполнении граничных условий:
EMBED
Equation.3
![]() — на поверхности контакта жидкость -
твердое тело и (или)p=p0
-
на свободной поверхности, где
EMBED Equation.3
— на поверхности контакта жидкость -
твердое тело и (или)p=p0
-
на свободной поверхности, где
EMBED Equation.3
![]() ,
р0
- заданные
величины
скорости твердого тела и внешнее
давление.
,
р0
- заданные
величины
скорости твердого тела и внешнее
давление.
Общего аналитического решения системы уравнений (2.21) — (2.24) не существует, и, как правило, в этом нет нужды, если речь идет о прикладных задачах. Обычно при решении конкретной инженерной задачи вводят ряд геометрических и физических допущений, не умаляющих, однако, основного характерного признака движения. Здесь важно свести уравнения и граничные условия к простейшему виду так, чтобы сохранить лишь главную цель задачи. Если все же граничная задача оказывается сложной, неподдающейся точному аналитическому решению, то применяют какой-либо приближенный метод решения или ставят эксперимент, используя для этого основные положения теории подобия.
В любом случае теоретической основой решения любой задачи гидромеханики является система уравнений (2.21) — (2.24) в том ином упрощенном виде.
