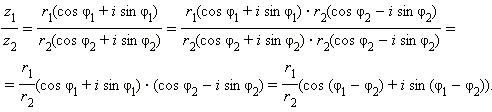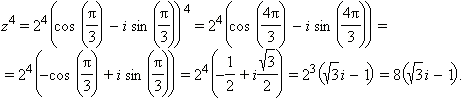Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)

Для разложения функции f(x) в ряд Маклорена нужно:

1) Найти производные ;

2) Вычислить значения производных в точке ;

3. Написать ряд

для заданной функции и найти его интервал сходимости;

4) Найти интервал (-R; R), в котором остаточный член ряда Маклорена . Если такой интервал существует, то в нем функцияf(x) и сумма ряда Маклорена совпадают.

Задание для самостоятельной работы:

1. Напишем формулу Тейлора и выражение остаточного члена для приn=4 и

2. Разложить по степеням х элементарные функции:

3. Разложить в ряд Маклорена функции:

1)

2)

3)

4)

Рекомендуемая литература: 1.1, 2.2. 2.5.

Самостоятельная работа №12

Тема: «Действия над комплексными числами»

Цель: Закрепление навыков выполнения арифметических действий над комплексными числами в алгебраической, тригонометрической и показательной форме.

Время выполнения: 2 часа

Теоретические сведения

Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1. Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда

   a = c и b = d.

2. Суммой двух комплексных чисел a + ib и c + id называется комплексное число

   a + c + i(b + d).

3. Произведением двух комплексных чисел a + ib и c + id называется комплексное число

ac – bd + i(ad + bc).

На комплексные числа можно смотреть как на многочлены с учётом равенства то и перемножать эти числа можно как многочлены. В самом деле,

то есть как раз получается нужная формула.

Пример 1 Вычислить z₁ + z₂ и z₁z₂, где z₁ = 1 + 2i и z₂ = 2 – i.

Решение:

Имеем

Ответ. z₁ + z₂ = 3 + i, z₁z₂ = 4 + 3i.

Геометрической интерпретацией действительных чисел является действительная прямая. Любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс откладывается действительная часть комплексного числа, а на оси ординат – мнимая часть.

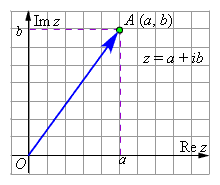
Любому комплексному числу z = a + ib соответствует вектор и наоборот, каждому векторусоответствует, и притом единственное, числоz = a + ib.

Модулем комплексного числа называется длина вектора, соответствующего этому числу:

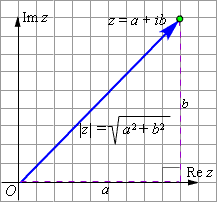
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.

Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.

Существует такое число z = 0, которое обладает свойством

z + 0 = z

Для любых двух чисел z₁ и z₂ существует такое число z, что z₁ + z = z₂. Такое число z называется разностью двух комплексных чисел и обозначается z = z₂ – z₁.

Для любого комплексного числа z:

z · 1 = z.

Для любых двух чисел исуществует такое числоz, что Такое числоz называется частным двух комплексных чисел и обозначается Деление на 0 невозможно.

Если число z = a + bi, то число называетсякомплексно сопряжённым с числом z. Комплексно сопряжённое число обозначается Для этого числа справедливы соотношения:

Пример 2 Найдите число, сопряжённое к комплексному числу (1 + 2i)(3 – 4i).

Решение:

Имеем . Следовательно,

Ответ. 11 – 2i.

Пример 3 Вычислите

Решение:

Имеем

Ответ. i.

Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть и φ = argz. Тогда по определению аргумента имеем:

Отсюда получается

z = a + bi = r(cos φ + i sin φ).

Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.

Пример 4 Записать число в тригонометрической форме.

Решение:

Найдём модуль этого числа: Аргумент данного числа находится из системы

Значит, один из аргументов числа равенПолучаем:

Ответ. 

Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим образом. Пусть z₁ = r₁(cos φ₁ + i sin φ₁) и z₂ = r₂(cos φ₂ + i sin φ₂). Имеем:

Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ₁, φ₂, ..., φ_n – аргументы чисел z₁, z₂, ..., z_n, то

В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.

Первая формула Муавра:

Пример 4 Вычислить если

Решение:

Данное число в тригонометрической форме имеет вид По первой формуле Муавра получаем:

Ответ. 

Число z называется корнем степени из комплексного числаw, если Корень степениобозначается. Пусть теперь числоw фиксировано. Найдём z из уравнения

Вторая формула Муавра:

Пример 5 Найти

Решение:

Представим число –1 в тригонометрической форме:

По второй формуле Муавра получаем:

Получаем последовательно:

Ответ.