Размерности и показатели степени при конвективном теплообмене

№ п/п	Наименование величины	Показатель степени	Размерности
			кг	м	с	К	Дж
1	l	il		1	0	0	0
2	u	iu	1	2	1	0	0
3		i	1	1	1	0	0
4		i	1	3	0	0	0
5		i	0	1	1	1	1
6	С	ic	1	0	0	1	1
7		1	0	2	1	1	1

Исключаем размерности:

1 — (кг) i_u + i_ + i_  i_c = 0

2 — (м) i_l  2i_u  i_  3i_  i_+ 2 = 0

3 — (c)  i_l i_  i_+ 1 = 0

4 — (К)  i_  i_c + 1 = 0

5 — (Дж) i_ + i_c  1 = 0.

Как видно из последних двух уравнений, полученных исключением размерности, они тождественны, т. к. определяются из теплоемкости воды. Таким образом, имеем 4 независимых уравнения связи при шести независимых переменных. Следовательно, в исходной системе уравнений только два неизвестных показателя подлежат экспериментальному определению, а остальные определяются по полученной системе уравнений в зависимости от этих двух основных. Например, в опыте определены показатели и они соответственно равны: i_u= n; i_c = m (n, m — число); тогда, используя систему уравнений, получим:

из 4 — i_= 1  i_c= 1  m

из 3 — i_ =  i_u  i_  1 = n + 1 + m  1 = m  n

из 1 — i_ = i_c  i_u  i_ = m  n  m + n = 0

из 2 — i_l = 2i_u + i_ + i_ + 3i_  2 = 2n + m  n +1  m  2 = n  1.

Подставив полученные значения показателей в (4.48), получим

(4.49)

Преобразуем полученные уравнения, сгруппировав величины с одинаковыми показателями

(4.50)

или

, (4.51)

где ul/μ = ωl/ν = Re — критерий Рейнольдса — критерий гидродина-мического подобия;

μС/λ = ν/a = Pr — критерий Прандтля — критерий теплофизического подобия;

αl/λ = Nu — критерий Нуссельта — критерий теплового подобия.

Таким образом, на основании теории размерностей получено уравнение связи безразмерных параметров, характеризующих теплообмен в условиях вынужденной конвекции и число независимых переменных снижено с 6 до 2, что обеспечивает возможность их экспериментального определения, и тогда N=Aⁿ=100.

Правильность использования теории размерностей подтверждается π-теоремой, исходя из чего физическое уравнение, содержащее n2 размерных величин, из которых m1 имеют независимые размерности, после приведения их к безразмерному виду должно содержать  безразмерных параметров  = n – m. В нашем случае  = n – m = 6 – 4 = 2. Численные значения постоянных, входящих в уравнение (4.51) С₀, n, m, определяются экспериментально и в зависимости от вида теплообмена приводятся в справочной литературе, некоторые даны в табл. 4.3.

4.3.3. Теория подобия

При использовании теории подобия необходимо иметь дифференциальное уравнение, описывающее исследуемый процесс. Проводя критериальную обработку этого уравнения, получают состав критериев подобия. Выявление состава критериев подобия осуществляется методом «губки»: в исходном дифференциальном уравнении опускаются знаки дифференциалов, полученные результаты приравниваются, выделяются независимые слагаемые, на основании которых определяются параметры подобия.

Для конвективного теплобмена (его математического описания) необходимо иметь: 1) дифференциальное уравнение движения вязкой несжимаемой жидкости — уравнение Навье — Стокса; 2) уравнение теплопроводности — Фурье — Кирхгофа; 3) уравнение теплообмена на границе твердая поверхность — окружающая среда — Био —Фурье.

Уравнение движения вязкой несжимаемой жидкости:

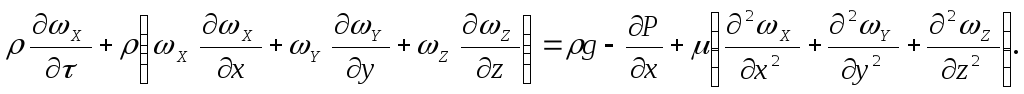(а)

Получаем на основании теории подобия с использованием метода «губки» 5 независимых комплексов (уравнение написано для одномерного потока по оси «Х»).

№ п/п	1	2	3	4	5
комплексы

Группируем полученные независимые комплексы и получаем критерии подобия:

делим 2:1 ; (4.52)

2:5 ; (4.53)

4:2 ; (4.54)

3:2 , (4.55)

где Но — критерий гомохронности — гидродинамический критерий одновременности событий;

Re — критерий Рейнольдса — параметр гидродинамического подобия режимов движения жидкости, характеризует соотношение сил инерции и сил вязкости;

Eu — критерий Эйлера — характеризует соотношение сил инерции и сил давления;

Fr — критерий Фруда — характеризует соотношение сил инерции и сил тяжести.

Следует отметить, что полученный основной состав критериев подобия Но, Re, Eu, Fr характеризует режим движения потока и может быть преобразован в любой иной состав критериев подобия умножением или делением исходного состава, но при этом в любом случае должно выполняться условие по возврату любого иного состава критериев подобия к исходному.

Так, вместо критерия Фруда можно использовать критерий Галилея:

(4.56)

или

, если , то (4.57)

(4.58)

Умножая критерий Ga на относительное изменение плотности (ρ – ρ₀/ρ₀), получим критерий Архимеда. Если ρ – ρ₀/ρ₀ = βΔТ происходит за счет разности температур ΔТ = Т₁ – Т₂, то получим критерий Грасгофа. Критерий Ar характеризует величину подъемной силы при изучении свободной конвекции жидкости, в которой находятся пузырьки, твердые частицы или капли другой жидкости. Критерий Ga используется вместо критерия Fr, т. к. в него входит скорость потока, которую трудно измерить.

Кроме того, оказывается, что часть критериев является зависимой — функцией других критериев. Так, критерий Eu зависит от Re, что получается из рассмотрения уравнения Дарси — Вейсбаха:

, (4.59)

откуда

, (4.60)

с другой стороны

. (4.61)

Вторым уравнением, описывающим процесс конвективного теплообмена при вынужденном движении, является уравнение теплопроводности

(б)

Применяя метод «губки», получим три независимых комплекса:

делим 2:3 ; (4.62)

3:1 . (4.63)

№ п/п	1	2	3
комплексы

Получаем критерии Пекле Pe и Фурье Fо. Критерий Pe характеризует соотношение тепловых потоков, переносимых конвекцией и теплопроводностью. Вместо критерия Pe можно использовать критерий Прандтля, т. к.

. (4.64)

Критерий Fо характеризует одновременность событий, так называемое безразмерное время. Из третьего уравнения теплообмена на границе твердая поверхность — окружающая среда получим критерий теплового подобия — критерий Нуссельта Nu:

(в)

№ п/п	1	2
комплексы

делим 2:1 . (4.65)

Таким образом, проведя критериальную обработку дифференциальных уравнений, получим состав критериев подобия:

Nu=(Ho, Fo, Re, Pe, Gr)=₁(Ho, Fo, Re, Pe, Gr). (4.66)

Связь между критериями определяется опытным путем. Следует заметить, что теории размерностей и подобия могут использоваться при изучении любых процессов (гидравлических, механических, экономических).

В табл. 4.2 приводятся критерии тепловых и гидродинамических процессов.

Таблица 4.2

Главнейшие безразмерные критерии тепловых и гидродинамических процессов

Формула	Название критерия	Величины, входящие в критерий	Значение критерия
	Критерий Рейнольдса (критерий режима движения)	  скорость потока, м/сек; d  эквивалентный диаметр канала;   коэффициент кинематической вязкости, м2/сек.	Характеризует гидродинамический режим движения
	Критерий Эйлера (критерий падения давления)	Р  перепад давления, Н/м2;   плотность жидкости, кг/м3.	Характеризует безразмерную величину падения давления
	Критерий Прандтля (критерий физических свойств жидкости)		Характеризует физические свойства жидкости и способность распространения тепла в жидкости
	Критерий Пекле		Является мерой отношения молекулярного и конвективного переноса тепла в потоке
	Критерий Нуссельта (критерий теплоотдачи)	  коэффициент конвективной теплоотдачи, Вт/(м2град)	Характеризует отношение между интенсивностью теплоотдачи и температурным полем в пограничном слое потока
	Критерий Био	l  характерный размер тела, м; м  коэффициент теплопроводности твердого тела, Вт/(мград)	Характеризует соотношение между внутренним и внешним термическим сопротивлениями
	Критерий Фурье (безразмерное время)	  время, сек	Характеризует связь между скоростью изменения температурного поля, физическими константами и размерами тела
	Критерий Грасгофа (критерий подъемной силы)	  коэффициент объемного расширения, 1/град; t  разность температур в двух точках системы потока и стенки, град	Характеризует кинематическое подобие при свободном движении жидкости