6. Статистический анализ сезонной компоненты

6.1. Методы выявления периодической компоненты

Для выявления периодической компоненты во временном ряду можно воспользоваться несколькими способами:

1) при применении метода Фостера — Стюарта на наличие периодичности рассчитывается показатель t_s: если t_s > t_α, то это говорит о том, что в ряду отклонений от тренда существуют колебания;

2) для определения периодичности можно использовать автокорреляционную функцию (1.9) (наличие временного лага τ показывает, что ряд содержит периодическую составляющую с периодом τ);

3) для длинных временных рядов можно применить критерий „пиков" и „ям", в основе которого лежит подсчет числа экстремальных точек p_t изучаемого ряда. Этот расчет осуществляется следующим образом:

1) выявляется последовательность

1, если y_t+1 < y_t > y_t-1 или y_t-1 > y_t < y_t+1,

0 в противном случае для всех t = 2, 3, …, n-1;

2) определяется , гдеn— число наблюдений;

3) проверяется гипотеза об отсутствии периодической компоненты путем сравнения расчетного значения р со значением

рассчитанным для случайного ряда. Если эти значения близки, то можно отказаться от дальнейшей проверки и признать временной ряд случайным;

4) еслиизначительно отличаются друг от друга, то про­изводится дальнейшая проверка гипотезы, основанная на подсчете фаз различной длины. Фазой называется интервал между двумя соседними индексами уровней, для которых (например, если для у₅ и , то фаза имеет длину; если для и, то фаза имеет длину ). Подсчитывается число фаз , ,длин,,. Теоретическое значениечисла фаз различной длины для случайного ряда равно:

5) рассчитывается значение . В случае трех групп это значение определяется по формуле

Если , то колебания исходного ряда можно считать случайными, если , то ряд содержит периодическую компо­ненту [20].

Пример 6.1. Используя данные табл. 6.1, проверим по значениям автокорреляционной функции, имеются ли в этом вре­менном ряду периодические колебания.

Таблица 6.1

Динамика продажи молочной продукции в регионе за 1996 – 1999 гг.

Год	Квартал
	I	II	III	IV
1996	54,6	80,6	78,8	53,5
1997	53,2	97,5	98,7	60,5
1998	56,4	112,1	114,5	74,6
1999	66,6	126,6	132,8	76,7

Для исследуемого ряда были рассчитаны значения автокорреляционной функции по формуле (1.9). Результаты приведены в табл. 6.2.

Таблица 6.2

Значения автокорреляционной функции

Сдвиги	1	2	3	4	5
Значения автокорреля- ционной функции	0,208	-0,464	0,115	0,611	0,030
95% граница	0,490	0,511	0,603	0,609	0,742

Из таблицы видно, что наибольшее значение автокорреляци­онная функция принимает на 4-м сдвиге. Это подтверждает на­личие сезонности, период которой равен IV кварталам, и превы­шение значения автокорреляционной функции уровня, определен­ного для 95% границы.

6.2. СТАТИСТИЧЕСКИЙ АНАЛИЗ СЕЗОННОСТИ

Одна из основных задач анализа временного ряда состоит в выделении сезонной компоненты (или сезонности). К сезонным относят такие явления, которые обнаруживают в своем развитии определенные закономерности, регулярно повторяющиеся из ме­сяца в месяц, или из квартала в квартал каждый год. Эти ко­лебания являются результатом природных, общественных и соци­ально-экономических факторов. Сезонные колебания проявляются с неодинаковой интенсивностью в различных сферах жизни об­щества: неодинаковое потребление электроэнергии в течение года; ярко выраженный сезонный характер сельского хозяйства, вызы­вающий неравномерность работы перерабатывающих предприятий, что в свою очередь обусловливает сезонные колебания в торговле. Сезонность также возникает из-за сезонного спроса на товары народного потребления (обувь, одежда) и т. д. Но как бы ни проявлялась сезонность, она всегда наносит ущерб деятельности фирм, который проявляется в неравномерном использовании обо­рудования и рабочей силы, неравномерной поставке сырья, за­грузке транспорта и т. д. Поэтому изучение сезонных колебаний необходимо для того, чтобы обеспечить стабильный ритм работы предприятий.

Сезонные колебания характеризуются специальным показате­лем — индексом сезонности . Совокупность этих показателей,вычисленных по месячным или по квартальным данным за не­сколько лет (не менее 3), отражает сезонную волну. В общем виде эти показатели определяются как процентное отношение фактического уровня ряда к некоторому теоретическому уровню, принятому за базу.

Если ряд динамики не содержит ярко выраженной тенденции в развитии, то индексы сезонности вычисляются непосредственно по фактическим данным без предварительного выравнивания (спо­соб постоянной средней). Для каждого месяца (квартала) рассчи­тывается средняя величина уровня затем вычисляется среднийуровень для всего ряда и определяется процентноесоотношение средних уровней для каждого месяца к общему среднему уровню ряда, т. е.

(6.1)

где =1, 2, ..., 12, если данные помесячные, или= 1, 2, 3, 4, если данные поквартальные.

Если ряд содержит определенную тенденцию в развитии, то прежде чем вычислить индекс сезонности, по фактическим уров­ням выявляется общая тенденция ряда, которая может быть вы­ражена с помощью аналитического выравнивания в виде матема­тической функции.

При использовании аналитического выравнивания ход вычис­лений индекса сезонности следующий:

1. находится подходящая функция выравнивания (п. 2.2.2);

2. для каждого месяца (или квартала) вычисляются теорети­ческие уровни 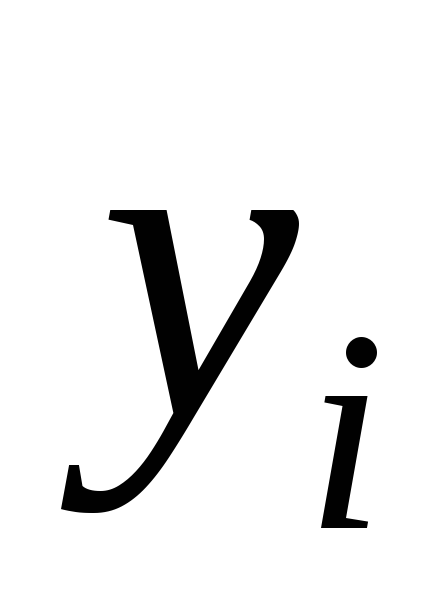, рассчитанные по уравнению тренда;

3) определяются показатели сезонности как процентное отно­шение фактического месячного (квартального) уровня , к соот­ветствующему расчетному уровню:

3. находится среднее арифметическое из показателей сезонно­сти по\ одноименным периодам (либо месяцам, либо кварталам):

,

где N — число одноименных периодов;

5) расчет индексов заканчивается проверкой, заключающейся в определении среднего индекса сезонности который должен быть равен 100 %. Но так как не всегда удается выделить влияние несезонных факторов (т. е.100 %), то следует произвести выравнивание индексов, которое заключается в умножении ин­дексов сезонности на величину, обратную среднему индексу се­зонности;

6) после определения выравненных индексов сезонности можно найти уровни временного ряда, в которых элиминировано влияние сезонности. Для этого нужно фактические уровни поде­лить на соответствующие выравненные индексы (в коэффициентах). Показателем колеблемости временного ряда за счет сезонности служит среднее квадратическое отклонение, вычисляемое по фор­муле

,

где т = 12 (если данные помесячные) либо т = 4 (если данные поквартальные).

Чем меньше значение , тем меньше влияние сезонного фак­тора на исследуемый показатель.

Для повышения устойчивости индексов сезонности можно рас­считать средний индекс сезонности по расположению. Для этого в ранжированном ряду показателей сезонности отбрасываются са­мые высокие и низкие значения и определяется средняя арифме­тическая из центральных значений индексов сезонности. Если чис­ло показателей четное, то в расчет берется 4 или 6 центральных точек, если нечетное, то 3 или 5.