Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Западный государственный заочный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика ч.1 (УМК 7,8).pdf

Скачиваний:

Добавлен:

16.02.2016

Размер:

2.14 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

3.2. Опорный конспект

Раздел 1. Тройные и поверхностные интегралы

Данный раздел включает три темы:

1.1.Тройные интегралы.

1.2.Поверхностные интегралы первого рода.

1.3.Поверхностные интегралы второго рода.

Вкаждой теме сначала излагается теоретический материал и приводятся иллюстрирующие примеры. Завершает тему подробный разбор решений типовых примеров.

После каждой темы Вам следует ответить на вопросы для самопроверки. По завершении работы над разделом необходимо решить тест №1. Студенты очно-заочной и заочной форм обучения должны сделать две задачи из контрольной работы № 7.

1.1. Тройные интегралы

При изучении данной темы Вам предстоит познакомиться со следующими вопросами:

•Определение тройного интеграла;

•Основные свойства тройных интегралов;

•Вычисление тройных интегралов;

•Применение тройных интегралов.

После изучения данных вопросов в опорном конспекте Вам следует

ответить на вопросы для самопроверки. Если Вы будете испытывать затруднения в ответах, обратитесь к [2] или к глоссарию. Студенты очнозаочной и заочной форм обучения должны решить задачу под №101-110 из контрольной работы № 7 в соответствии со своим вариантом.

Тройной интеграл представляет собой одно из возможных обобщений двойного интеграла. Аналогично тому, как задача о массе плоской пластины приводит к понятию двойного интеграла, задача о массе пространственного тела приводит к понятию тройного интеграла. Подробно эта задача рассмотрена в [2,3].

Определение тройного интеграла

Пусть в некоторой пространственной области T задана функция f (x, y, z) . Проделаем следующие операции:

1. Разобьем область Т на п частей		T1,	T2 ,..., Tn . Обозначим
объемы и диаметры этих частей	V1,	V2 ,...,	Vn и λ1, λ2 ,..., λn
соответственно. Наибольший из λ1, λ2 ,..., λn		обозначим через λ.
	15

интеграл обозначают символами

тройным интегралом от функции

2. Выберем произвольно в каждой области Ti (i =1, 2,...n) по точке

(xi , yi , zi ) и вычислим f (xi , yi , zi ).

3.Найдем сумму

∑ f (xi , yi , zi ) Vi .

i=1

Эта сумма называется интегральной суммой для функции f (x, y, z) в

области T .

4. Вычислим lim ∑ f (xi , yi , zi ) Vi .

λ→0 i=1

Если этот предел существует, конечен и не зависит ни от способа разбиения области Т на части, ни от выбора точек (xi , yi , zi ), то он называется f (xi , yi , zi ) пo области Т. Тройной

∫∫∫ f (x, y, z)dv или ∫∫∫ f (x, y, z)dxdydz.

T T

При этом используют следующие названия:

f (x, y, z) - подынтегральная функция, Т - область интегрирования,

x, y, z - переменные интегрирования, dv или dxdydz - элемент объема. Таким образом, определение тройного интеграла можно записать так

∫∫∫ f (x, y, z)dxdydz = lim		n
∫∫∫ f (x, y, z)dxdydz = lim		∑ f (xi , yi , zi ) Vi .	(1.1)
T	λ→0 i=1
Механический смысл тройного интеграла
Если в некоторой	области Т	трехмерного пространства	определена

неотрицательная функция μ(x, y, z) , которая задает плотность распределения массы в теле Т, то тройной интеграл ∫∫∫μ(x, y, z)dxdydz определяет массу

T
тела Т, т.е.
M = ∫∫∫μ(x, y, z)dxdydz.	(1.2)
T
Достаточное условие существования тройного интеграла
Приведем без доказательства следующую теорему.
Теорема 1.1. Если функция f (x, y, z) непрерывна в замкнутой области
T , ограниченной кусочно-гладкой поверхностью, то тройной	интеграл
∫∫∫ f (x, y, z)dxdydz cyществует.
T

Основные свойства тройных интегралов

Свойства тройных интегралов аналогичны свойствам двойных и также легко выводятся из определения тройного интеграла. Перечислим их, предполагая, что все встречающиеся ниже функции удовлетворяют условиям теоремы 1.1 в рассматриваемых областях.

1. ∫∫∫dxdydz =V , где V - объем области Т;

2. ∫∫∫kf (x, y, z)dxdydz = k ∫∫∫ f (x, y, z)dxdydz ;

T T

3. ∫∫∫ f (x, y, z)+g(x, y, z) dxdydz =∫∫∫f (x, y, z)dxdydz +∫∫∫g(x, y, z)dxdydz.

T T T

Из свойств 2 и 3 следует свойство линейности тройного интеграла:

∫∫∫ k1 f (x, y, z)+k2g (x, y, z) dxdydz =k1∫∫∫ f (x, y, z)dxdydz +k2 ∫∫∫g(x, y, z)dxdydz.

T T T

4. Свойство аддитивности.

Если область Т разбита на две части T1 и T2 , имеющие лишь общую

границу, то

∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (x, y, z)dxdydz + ∫∫∫ f (x, y, z)dxdydz .

5.Если f (x, y, z) ≥ 0 всюду в области Т, то

∫∫∫f (x, y, z)dxdydz ≥ 0 .

			T
6.	Если		f (x, y, z) ≥ g(x, y, z)		всюду в области Т, то
			∫∫∫ f (x, y, z)dxdydz ≥ ∫∫∫g (x, y, z)dxdydz .
			T		T
7.		∫∫∫ f (x, y, z)dxdydz		≤ ∫∫∫	f (x, y, z)	dxdydz .
7.		∫∫∫ f (x, y, z)dxdydz		≤ ∫∫∫	f (x, y, z)	dxdydz .
		T		T

8. Теорема о среднем. Если функция f (x, y, z) непрерывна в замкнутой

ограниченной области Т, то в этой области найдется хотя бы одна такая точка (x, y, z ), чтовыполняется равенство ∫∫∫ f (x, y, z)dxdydz = f (x, y, z )V ,

где V - объем области Т.

Вычисление тройных интегралов

Вычисление тройных интегралов в декартовых координатах


	Вычисление тройных		интегралов
аналогично		вычислению	двойных и	z	z = H (
основывается на следующей теореме,
которую мы приведем без доказательства.
которую мы приведем без доказательства.
Теорема 1.2. (Фубини) Пусть замкнутая
пространственная область Т (рис. 1.1)
ограничена цилиндрической поверхностью
с образующими, параллельными оси Oz, и
с образующими, параллельными оси Oz, и
двумя	поверхностями,		задаваемыми	O
уравнениями		z = h(x, y) и	z = H(x, y) ,	O
причем функции h(x,y) и Н(х,у) непрерывны				x	D
в области D, где D - проекция области Т на
плоскость Оху, и удовлетворяют в этой					Рис. 1.1
области неравенству h(x, y) ≤ H(x, y) .

x, y)

z = h(x, y)

Тогда для любой функции f (x, y, z) , непрерывной в области Т, справедливо равенство:

		H ( x, y )
∫∫∫	f (x, y, z )dxdydz = ∫∫	∫
T	D	h ( x , y )

Эту формулу принято записывать так

f (x, y, z )dz dxdy.

∫∫∫ f (x, y, z )dxdydz = ∫∫dxdy		H ( x, y)	(x, y, z )dz.
∫∫∫ f (x, y, z )dxdydz = ∫∫dxdy		∫ f	(x, y, z )dz.	(1.3)
T	D	h( x, y)

При этом сначала вычисляется внутренний интеграл по переменной z при постоянных х и у, а затем берется двойной интеграл по переменным х и у. Так,

например,	если	область		D	ограничена	линиями
x = a, x = b,	y = ϕ(x),	y = ψ(x),	где	a < b , а	ϕ(x) ≤ ψ(x), то, переходя
от двойного интеграла к повторному, получим формулу
		b	ψ(x)	H ( x, y, z)
∫∫∫ f (x, y, z)dxdydz = ∫dx			∫	dy ∫	f (x, y, z)dz. .	(1.4)
T		a	ϕ(x)	h( x, y, z)

Выражение, стоящее в правой части равенства (1.4), называется повторным (трехкратным) интегралом.

В этом случае сначала вычисляется внутренний интеграл по переменной z при постоянных х и у, затем полученная функция двух переменных х и у интегрируется по переменной у при постоянном х, и, наконец, полученная функция интегрируется по х в пределах от а до b.

Если область Т ограничена цилиндрическими поверхностями с образующими, параллельными осям Ох или Оу, то справедливы теоремы, аналогичные теореме 1.2.

Теорема 1.3. Пусть замкнутая область Т ограничена цилиндрической поверхностью с образующими, параллельными оси Ох, и двумя поверхностями,

задаваемыми уравнениями x = h (y, z) и x = H (y, z), причем функции h(y,z)

иH ( y, z) непрерывны в области D, где D - проекция области Т на плоскость Oyz,

иудовлетворяют в этой области неравенству h(x, y) ≤ H(x, y) .

Тогда для любой функции	f (x, y, z) , непрерывной в		области Т,
справедливо равенство:		H ( y,z)
		H ( y,z)
∫∫∫ f (x, y, z)dxdydz = ∫∫dydz		∫ f (x, y, z)dx.	(1.5)
T	D	h( y,z)

Теорема 1.4. Пусть замкнутая область Т ограничена цилиндрической поверхностью с образующими, параллельными оси Оу, и двумя поверхностями,

задаваемыми	уравнениями y = h (x, z)			и	y = H (x, z), причем функции
h(x, z) и H (x, z)		непрерывны в области D, где D -проекция области Т на
плоскость	Oxz,	и	удовлетворяют	в	этой	области	неравенству
h(y, z) ≤ H (y, z).
Тогда	для любой		функции f (x, y, z) , непрерывной в				области Т,
справедливо равенство:					H ( x,z)
	∫∫∫ f (x, y, z)dxdydz = ∫∫dxdz				H ( x,z)	f (x, y, z)dy.
	∫∫∫ f (x, y, z)dxdydz = ∫∫dxdz				∫	f (x, y, z)dy.	(1.6)
	T		D		h( x,z)

Вформуле(1.5) интегралпо dx - внутреннийиберетсяприпостоянных y и z . Аналогично в формуле (1.6) интеграл по dy - внутренний и вычисляется при постоянных х и z. Если область Т имеет более сложный вид, то, чтобы

вычислить интеграл, ее следует разбить на конечное число частей, каждая из которых удовлетворяет условиям одной из теорем 1.1-1.4. Далее нужно вычислить интегралы по этим частям. Исходный интеграл будет равен сумме интегралов по частям.

Пример 1.1. Вычислить ∫∫∫12xzdxdydz , по области Т, ограниченной

параболическим цилиндром y = x2 и плоскостями z = 0, y + z =1, x =0, при x ≥ 0.

Решение. Изобразим область Т (рис. 1.2). Она ограничена с боков цилиндрической поверхностью с образующими, параллельными оси Oz

(параболический цилиндр y = x2 и координатная плоскость x = 0 ), а снизу и

сверху	поверхностями		z = 0 и	z =1− y .	Поэтому можно					воспользоваться
формулой		(1.3).	Область	D	изображена							на					рис.1.3.
		z				y
		z
	y = x2		y + z =1		1
					1


		O	1	y												x
	1			y	O					1
	1
x		Рис. 1.2					Рис. 1.3
Таким образом,				1− y
				1− y										1− y
	∫∫∫12 xzdxdydz = ∫∫dxdy ∫ 12 xzdz = ∫∫dxdy 6 xz 2																=

														0
	T		D	0	D
			1	1	1		x(1		− y)						3	1
			1	1	1										3	1
	= 6∫∫x(1− y)2 dxdy = 6∫dx ∫ x(1− y)2 dy = −6∫dx																=
	= 6∫∫x(1− y)2 dxdy = 6∫dx ∫ x(1− y)2 dy = −6∫dx								3								=
	D		0	x2	0				3							x2
				x2				1								x2
		= 2∫1 x(1− x2 )3 dx =∫1 (1− x2 )3 dx2 =− (1− x2 )4							=		1		.
											1
										4
		0	0		4					4
		0	0					0

Замена переменных в тройном интеграле

Формула перехода в тройном интеграле к новым координатам аналогична формуле перехода для двойного интеграла.

Рассмотрим две прямоугольные системы координат Oxyz и Ouvw и две замкнутые ограниченные области: Т - в системе Oxyz, τ - в системе Ouvw. Пусть функции

x = ϕ(u,v, w), y = ψ(u,v, w), z = χ(u,v, w)

(1.7)

устанавливают взаимно однозначное отображение области τ на область Т. Тогда, если функции (1.7) имеют непрерывные частные производные в

области τ, то справедливо равенство:

∫∫∫f (x, y, z)dxdydz =

T
= ∫∫∫ f (ϕ(u, v, w), ψ(u, v, w)χ(u, v, w)) I (u, v, w) dudvdw,	(1.8)

		∂ ϕ	∂ ϕ	∂ ϕ
		∂ ϕ	∂ ϕ	∂ ϕ
		∂ u	∂ v
		∂ u	∂ v	∂ w
где	I (u , v , w ) =	∂ ψ	∂ ψ	∂ ψ	.
где	I (u , v , w ) =	∂ u	∂ v	∂ w	.
		∂ χ	∂ χ	∂ χ
		∂ u	∂ v
		∂ u	∂ v	∂ w

Так же, как и для двойного интеграла, I(u,v,w) называется якобианом (определителем Якоби) преобразования (1.7).

Можно показать, что модуль якобиана равен коэффициенту изменения (увеличения или уменьшения) элементарных объемов в рассматриваемой точке.

Переход в тройном интеграле к цилиндрическим координатам
Рассмотрим один частный случай преобразования координат (1.7)
x = ρcos ϕ, y = ρsin ϕ, z = z.	(1.9)

Эти преобразования соответствуют переходу от прямоугольной системы Oxyz к цилиндрической системе координат Oρϕz , у которой полюс совпадает с началом координат О, а полярная ось ρ совпадает с положительной полуосью

Ох (рис. 1.4).

Вычислим якобиан преобразования (1.9):

I (ρ,ϕ, z)=	cos ϕ	−ρsin ϕ	0
	cos ϕ	−ρsin ϕ	0
	sin ϕ	ρcos ϕ	0	= ρ.
	0	0	1

Подставляя полученное значение в
формулу (1.8), получаем формулу перехода в					ϕ
тройном	интеграле	к	цилиндрическим	x	ρ
координатам:				x	Рис.1.4

∫∫∫ f (x, y, z)dxdydz = ∫∫∫ f (ρcos ϕ,ρsin ϕ, z)ρdρdϕdz.

T T

(1.10)

Чтобы вычислить интеграл в цилиндрических координатах, переходят к повторному, используя для расстановки пределов геометрический смысл цилиндрических координат. Так, если область Т ограничена цилиндрической поверхностью с образующими, параллельными оси Oz, и поверхностями,

задаваемыми уравнениями z = h(x, y) и z = H (x, y), h(x, y) ≤ H (x, y) в

области D, где D - проекция области Т на плоскость Оху, то интеграл (1.10) равен

	H (ρcos ϕ,ρsin ϕ, z )	f (ρcos ϕ, ρsin ϕ, z )ρdz.
∫∫d ϕd ρ	∫	f (ρcos ϕ, ρsin ϕ, z )ρdz.	(1.11)
D	h(ρcos ϕ,ρsin ϕ, z )

Далее переходим во внешнем двойном интеграле к повторному, используя формулу расстановки пределов в полярных координатах для двойного интеграла. Внутренний интеграл выражения (1.11) вычисляем по переменной z при постоянных ρ и ϕ.

Пример 1.2. Вычислить тройной интеграл							∫∫∫dxdydz2 − x по области Т,
							T
задаваемой неравенствами x2 + y2 ≤ 2y,					x ≥ 0 , z ≥ 0 , x + z ≤ 2.
		z	x + z = 2			y
		z					x2 + y2 = 2 y
					2
	2				2
	2			x2 + y2 = 2 y
				x2 + y2 = 2 y
	O			y			x


			2		O
x			Рис. 1.5				Рис. 1.6

Решение. Область Т изображена на рис. 1.5, а ее проекция D на плоскость Оху - на рис. 1.6. Используя формулы (1.10) и (7.11), перейдем к цилиндрическим координатам:

										π
	dxdydz			2−ρcos ϕ			1			2sin ϕ			2−ρcos ϕ						ρdz
∫∫∫	dxdydz	= ∫∫dϕdρ ∫					1		ρdz =∫2 dϕ		∫		dρ	∫					ρdz	=
∫∫∫	2 − x	= ∫∫dϕdρ ∫			2		−ρcos ϕ		ρdz =∫2 dϕ		∫		dρ	∫				2 −ρcos ϕ		=
T	2 − x	D		0	2		−ρcos ϕ			0	0			0				2 −ρcos ϕ
T		D		0						0	0			0
	π						2−ρcos ϕ		π				π				2sin ϕ
		2sin ϕ		ρdρ					2sin ϕ					ρ2


	= ∫2 dϕ ∫					z		=∫2 dϕ ∫ ρdρ =∫2 dϕ											=
	= ∫2 dϕ ∫		2	−ρcos ϕ		z	0	=∫2 dϕ ∫ ρdρ =∫2 dϕ						2					=
	0	0	2	−ρcos ϕ					0	0			0	2			0
	0	0							0	0			0				0
		π		π											π
		2		2							1				π			π
		2		2											2
	= ∫2sin2 ϕdϕ = ∫(1 −cos 2ϕ)dϕ =														2
										ϕ−		sin 2ϕ				=			.
										ϕ−	2	sin 2ϕ				=		2	.
		0		0											0
		0		0											0

Применение тройных интегралов

С помощью тройного интеграла можно вычислить по известной плотности вещества такие физические характеристики, как масса тела, его статические моменты, моменты инерции, координаты центра масс.

Приведем формулу для вычисления массы тела.

Если μ(x, y, z) плотность тела Т, то с помощью тройного интеграла

вычисляется масса тела Т :
M = ∫∫∫μ(x, y, z)dxdydz .	(1.12)
T

Пример 1.3. Найти массу тела Т, задаваемого неравенствами

x2 + y2 ≤1, x ≥ 0, y ≥ 0 ,		0 ≤ z ≤ 4 − x2 , если
его плотность μ =	15		.
	(x + 2)	x +1

Решение. Тело Т изображено на рис. 7.7. Для нахождения его массы воспользуемся формулой (7.12):

z = 4 − x2

z 4

x2 + y2 =1

O 1

1 Рис. 1.7

		15					1		1−x2	4−x2				15
M = ∫∫∫		15				dxdydz = ∫dx			∫ dy	∫				15		dz =
M = ∫∫∫	(x + 2)					dxdydz = ∫dx			∫ dy	∫		(x + 2)				dz =
T	(x + 2)			x +1			0		0	0		(x + 2)			x +1
	1	1−x	2			z		4−x2	1		1−x		2	2 − x
			2					4−x2					2

=15∫dx ∫				dy					=15∫dx ∫						dy =
=15∫dx ∫				dy	(x +2)		x +1		=15∫dx ∫					x +1	dy =
	0	0						0	0		0
	0	0						0	0		0

=15∫

2 − x

1−x2

2 − x

1−x2

=15∫

∫ dy =15∫

dx y

x +1

(2 − x) 1 − x2

dx =15

1 (2 − x)

1 − x dx =151

1 +

(1 − x) 1

− x dx =

x +1

∫

1		3		(	− x	)	3	2		(	− x	)	5	2	1
1		3		(		)	3	2		(		)	5	2	1
=15∫ 1	− x −	(1 − x) dx =15	−	2 1					+	2 1						= 4.
=15∫ 1	− x −	(1 − x) dx =15	−						+							= 4.
0					3						5
															0
															0

Решение задач

Задача 1.1. Перейти от тройного интеграла ∫∫∫μ(x, y, z)dxdydz к

повторному (одним способом), где тело Т задается неравенствами x2 ≤ y ≤ x ;

0 ≤ z ≤ 4 − x2 − y2 .

Oxy	Решение. Тело Т изображено на рис. 1.8, а его проекция D на плоскость
Oxy	- на рис. 1.9.	Сбоку тело Т ограничено параболическим цилиндром
y = x2 и плоскостью		y = x , снизу плоскостью z = 0 , сверху – частью сферы
z =	4 − x2 − y2 .
	z	z = 4 − x2 − y2
		y	y = x
y = x2			y = x2

y = x	y	1	x
x
Рис.1.8		Рис. 1.9

Воспользуемся формулой (1.3), а затем расставим пределы в двойном интеграле по области D .

∫∫∫μ(x, y, z)dxdydz = ∫∫dxdy			4−x2 −y2				1	x	4−x2 −y2
∫∫∫μ(x, y, z)dxdydz = ∫∫dxdy				∫		f (x, y, z)dz = ∫dx ∫dy			∫	f (x, y, z)dz.
T	D			0			0	x2	0
									z
Задача 1.2. Вычислить ∫∫∫			1		dxdydz		по
Задача 1.2. Вычислить ∫∫∫		x +2			dxdydz		по			x = y
	T	x +2					z = 4 − x2
области T , ограниченной параболическими
цилиндрами	z = 4 − x2 ,			x =		y	и			y
плоскостями z = 0, y = 0 .										y
плоскостями z = 0, y = 0 .
							x	2
							x		Рис. 1.10
									Рис. 1.10
						24

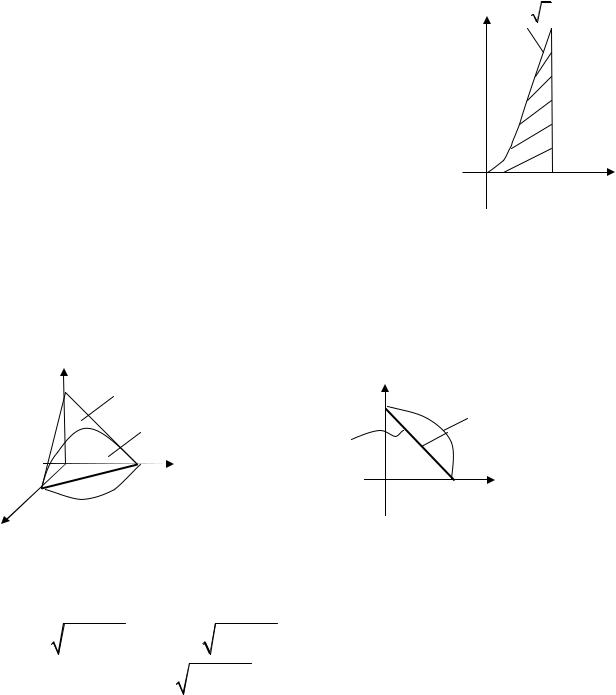
Решение. Область T изображена на рис. 1.10. Она ограничена с боков плоскостью y = 0 и параболическим цилиндром, а снизу и сверху

поверхностями z = 0 и z = 4 − x2 . Воспользуемся формулой (1.3) и вычислим внутренний интеграл по dz .

	1		4−x2	1	1			4−x2		4 − x2

∫∫∫		dxdydz = ∫∫dxdy	∫		dz = ∫∫dxdy		z		= ∫∫	x + 2 dxdy .
	x + 2			x + 2		x + 2		0
T		D	0		D				D

Теперь расставим пределы в двойном интеграле, беря за внешнюю переменную x . Область D изображена на рис.1.11.

2	x2		2						0x2		2					y	x = y (y = x2 )
∫dx ∫(2 − x)dy = ∫(2 − x)dx y											= ∫(2 − x)x2 dx =


0	0		0								0
	2			2x	3		x	4		2		16			1
										2


	= ∫(2x2	− x3 )dx =				−					=		− 4	=1		.
	= ∫(2x2	− x3 )dx =				−					=		− 4	=1		.
	0			3		4				0	3			3
	0									0
Задача		1.3.	Перейти				в			тройном				интеграле
																O	2	x
∫∫∫ f (x, y, z)dxdydz к цилиндрическим координатам и																	Рис. 1.11
T																	Рис. 1.11

расставить пределы интегрирования. Область T задается

неравенствами:

Решение.

плоскость Oxy

x2 + y2 ≤ (z −2)2 ; x + y ≥ 2; z ≥ 0 .

Тело T изображено на рис. 1.12, а его проекция D на

- на рис. 1.13.

	z	x2 + y2 = (z −2)2				y
	2	x2 + y2 = (z −2)2				y
	2					2	x2 + y2 = 4
		x + y = 2				2	x2 + y2 = 4
		x + y = 2
		y				x + y = 2
	O	y					x
2	O	2				O	x
						O	2
							2
x		Рис. 1.12					Рис. 1.13
x
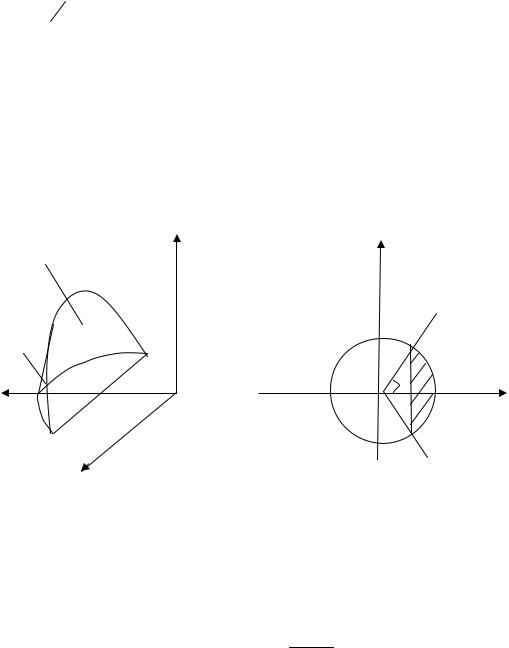
Тело T	ограничено сверху			конусом		x2 + y2 = (z −2)2 . Выразим		из	этого
уравнения		переменную	z	и	перейдем к		координатам ρ	и	ϕ:
z −2 = ±		x2 + y2 ; z = 2 ±		x2 + y2 .		Так как для рассматриваемой части
конуса z ≤ 2 , то z = 2 −			x2 + y2		или z = 2 − ρ .
						25

		2−ρ
Тогда ∫∫∫ f (x, y, z)dxdydz = ∫∫dϕdρ ∫ f (ρcos ϕ,ρsin ϕ, z)ρdz .
T	D	0

Для расстановки пределов в интеграле по области D перепишем уравнения линий, ограничивающих эти области в координатах ρ и ϕ:

x2 + y2 =4 ρ2 =4 ρ=2;						2
			x + y =2 ρcosϕ+ρsinϕ=2 ρ=					.
			x + y =2 ρcosϕ+ρsinϕ=2 ρ=				cosϕ+sinϕ	.
Следовательно,
	π		2		2−ρ
∫∫∫ f (x, y, z )dxdydz = ∫2 dϕ			2		2−ρ	(ρcos ϕ,ρsin ϕ, z )ρdz .
∫∫∫ f (x, y, z )dxdydz = ∫2 dϕ			∫		dρ ∫ f	(ρcos ϕ,ρsin ϕ, z )ρdz .
T	0		2		0
		cos ϕ+sin ϕ
Задача 1.4.	Вычислить			∫∫∫dxdydz		по области T , задаваемой
				T

неравенствами x2 + y2 ≤ 4 0 ≤ z ≤ x −1 .

	z = x −1		z	y
	z = x −1
					π
x2 + y2 = 4					3
x2 + y2 = 4
x	2	1	O	O 1	2	x
	2	1	O	O 1	2	x
			y
	Рис. 1.14			Рис. 1.15
Решение. Область T			изображена на рис.	1.14, а ее проекция		D на

плоскость Oxy - на рис. 1.15. Используя формулы (1.10) и (1.11), перейдем к цилиндрическим координатам. Для расстановки пределов в интеграле перепишемуравненияповерхностей, ограничивающихтеловкоординатах ρ и ϕ: z = x −1 z = ρcos ϕ−1; x =1 ρcos ϕ =1 ρcos1 ϕ. Тогда

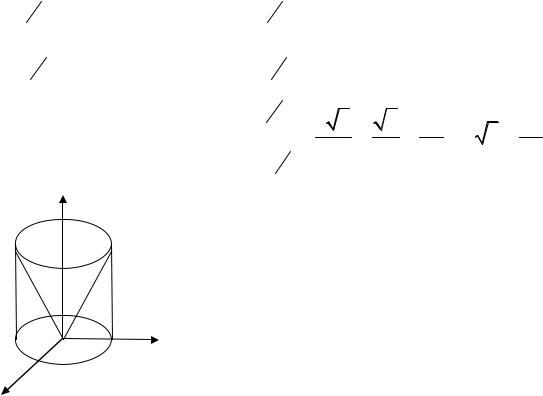
ρcos ϕ−1

∫∫∫dxdydz = ∫∫dϕdρ

∫

ρdz = ∫∫dϕdρρz

ρ(ρcos ϕ−1)dρ =

= ∫

dϕ

∫

cos ϕ− 2

−

dϕ =

3cos

2cos

−π

cos ϕ

	8		1
=		sin ϕ− 2ϕ+		tgϕ
=	3	sin ϕ− 2ϕ+	6	tgϕ
	3		6

π3

−π3

= 8 33 + 33 − 43π = 3 3 − 43π.

z	Задача 1.5. Найти массу тела Т, ограниченного
z		x2 + y2 = z2				плоскостью z = 2 , если
2	конусом	x2 + y2 = z2			и	плоскостью z = 2 , если
2	плотность μ(x, y, z) = x2 + y2 .
	плотность μ(x, y, z) = x2 + y2 .
	Решение. Воспользуемся формулой (1.12):
y		M = ∫∫∫(x2 + y2 )dxdydz.
O			T
2	Перейдем к цилиндрическим координатам и
x	расставим пределы в повторном интеграле, учитывая
Рис. 1.16	вид тела Т (рис. 1.16):
	2 π	2	2				02 π		2				ρ2 =
	2 π	2	2						2
M = ∫∫∫ρ2 ρd ϕd ρdz = ∫ d ϕ∫ρ3 d ρ∫dz = ϕ									∫ρ3 d ρ z


T	0	0	ρ						0
T	0	0	ρ						0
2			2ρ4	−	ρ5			2	=	16	π	.
2

= 2π∫ρ3 (2 − ρ)d ρ = 2π			4		5			0		5
0
0

Вопросы для самопроверки по теме 1.1

1.Дайте определение тройного интеграла.

2.В чем состоит механический смысл тройного интеграла?

3.Перечислите свойства тройного интеграла.

4.Чему равен якобиан преобразования при переходе от декартовых координат к цилиндрическим?

5.Какие механические величины можно вычислить, используя тройные интегралы?

6. Определите, чему равен ∫∫∫dxdydz , не вычисляя его, если T - область,

ограниченная координатными плоскостями и плоскостью x + y + z = 6 .

1.2. Поверхностные интегралы первого рода

При изучении данной темы Вам предстоит ознакомиться со следующими вопросами:

•Определение поверхностного интеграла первого рода.

•Основные свойства поверхностных интегралов первого рода.

•Вычисление поверхностных интегралов первого рода.

После изучения данных вопросов в опорном конспекте Вам следует

ответить на вопросы для самопроверки. Если Вы будете испытывать затруднения в ответах, обратитесь к [2] или к глоссарию. Студенты очнозаочной и заочной форм обучения должны решить задачу под № 111-120 из контрольной работы № 7 в соответствии со своим вариантом.

Поверхностные интегралы первого рода представляют собой такое же обобщение двойного интеграла, каким криволинейные интегралы первого рода являются по отношению к определенным интегралам. Аналогично тому, как задача определения массы материальной кривой привела к понятию криволинейного интеграла первого рода, так задача определения массы поверхности приводит к понятию поверхностного интеграла первого рода.

Определение поверхностного интеграла первого рода

Пусть в пространстве задана кусочно-гладкая поверхность σ, в точках которой определена функция f (x, y, z) . Проделаем следующие операции:

1.Разобьем поверхность σ сетью произвольно проведенных кривых

на п частей		σ1, σ2 ,...,	σn. Обозначим площади и диаметры этих частей
через	S1,	S2 ,..., Sn	и λ1, λ2 ,..., λn соответственно. Наибольший из
диаметров обозначим через λ.
	2. В каждой области		σi (i =1, 2,..., n) выберем произвольно по точке

Mi (xi , yi , zi ) и вычислим f (xi , yi , zi ). 3. Найдем сумму

∑ f (xi , yi , zi ) Si .

i=1

Эта сумма называется интегральной суммой для функции f (x, y, z) на

поверхности σ.

4. Вычислим lim ∑ f (xi , yi , zi ) Si .

λ→0 i=1

Если этот предел существует, конечен и не зависит от способа разбиения поверхности σ на части и от выбора точек Mi , то он называется

поверхностным интегралом первого рода от функции f (x, y, z) пo

поверхности σ. Этот интеграл обозначают символом

∫∫ f (x, y, z)dσ.

При этом используют следующие названия:

f (x, y, z) - подынтегральная функция, σ - поверхность интегрирования. Таким образом, можно записать


∫∫ f (x, y, z)dσ = lim		n
∫∫ f (x, y, z)dσ = lim		∑ f (xi , yi , zi ) Si.	(1.13)
σ	λ→0 i=1

Механический смысл поверхностного интеграла первого рода и его приложения

Если в каждой точке M (x, y, z) материальной поверхности σ плотность

вещества равна μ(x, y, z), то масса m поверхности σ определяется поверхностным интегралом первого рода

m = ∫∫μ(x, y, z)dσ.	(1.14)
σ

Кроме массы с помощью поверхностного интеграла первого рода можно вычислить статические моменты материальной поверхности, ее моменты инерции относительно координатных плоскостей и координаты центра тяжести. Поверхностный интеграл используется при решении задачи о притяжении материальной точки материальной поверхностью.

Достаточные условия существования поверхностного интеграла

первого рода
Приведем без доказательств теорему существования.
Теорема 1.5. Если	поверхность	σ	может	быть задана	уравнением
z = z (x, y), где функция	z (x, y) и	ее	частные	производные	z′x (x, y) и

z′y (x, y) непрерывны в замкнутой ограниченной области D на плоскости Oxy ,

а функция f (x, y, z) непрерывна на поверхности σ, то интеграл

∫∫ f (x, y, z)dσ существует.

Можно сформулировать еще две аналогичные теоремы, которые получаются из этой перестановкой переменных x,y,z.

Основные свойства поверхностных интегралов первого рода

Перечислим свойства поверхностных интегралов, предполагая, что все встречающиеся ниже поверхности и функции удовлетворяют условиям теоремы существования. Доказательства этих свойств легко получаются непосредственно из определения.

	1.	∫∫dσ = Sσ , где Sσ - площадь поверхности σ.
		σ
	2.	∫∫kf (x, y, z)dσ = k ∫∫ f (x, y, z)dσ.
		σ		σ
	3.	∫∫[f (x, y, z) + g(x, y, z)]dσ = ∫∫ f (x, y, z)dσ+ ∫∫ g(x, y, z)dσ.
		σ			σ	σ
∫∫[	Из свойств 2 и 3 следует свойство линейности поверхностного интеграла
	k f (x, y, z) + k		2	g(x, y, z) dσ = k		f (x, y, z)dσ+ k	2	∫∫	g(x, y, z)dσ.
	1		2	]	1 ∫∫		2	∫∫
σ	4.	Свойство аддитивности.			σ			σ
	4.	Свойство аддитивности.
	Если поверхность σ разбить на две части σ1 и σ2 , то
		∫∫ f (x, y, z)dσ = ∫∫ f (x, y, z)dσ+ ∫∫ f (x, y, z)dσ.
		σ		σ1		σ2
	5.	Если f (x, y, z) ≤ g(x, y, z) во всех точках поверхности σ, то

∫∫ f (x, y, z)dσ ≤ ∫∫ g(x, y, z)dσ.

σσ

6.∫∫ f (x, y, z)dσ ≤ ∫∫ f (x, y, z) dσ.

σσ

7.Теорема о среднем

Если функция f (x, y, z) непрерывна на поверхности σ, то на этой поверхности найдется хотя бы одна такая точка (x, y, z ) , что

∫∫ f (x, y, z)dσ = f (x, y, z )Sσ,

где Sσ - площадь поверхности σ.

Вычисление поверхностных интегралов первого рода

Вычисление поверхностных интегралов первого рода сводится к вычислению двойных интегралов. Приведем формулу перехода от поверхностного интеграла к двойному.

Обозначим через D проекцию поверхности σ на плоскость Оху. Рассмотрим случай, когда D - замкнутая ограниченная область. Пусть далее поверхность σ задается уравнением z = z(x, y), причем функция z(x, y) и ее

частные производные z′x (x, y),

z′y (x, y) непрерывны в области D. Тогда

∫∫

f (x, y, z)dσ=

∫∫

(

x, y, z(x, y)

)

+ z′

(x, y) 2

+ z′

(x, y) 2 dxdy.

(1.15)

Выражение

dσ = 1+[z′x ]2 + z′y

2 dxdy

(1.16)

называется дифференциалом площади поверхности.

Имеют место еще две аналогичные формулы для перехода от поверхностного интеграла к двойному, которые получаются перестановкой переменных x,y,z.

В случае, когда разные части поверхности σ задаются разными уравнениями, то нужно воспользоваться свойством аддитивности поверхностного интеграла, т.е. разбить поверхность σ на соответствующее

число частей, вычислить интегралы по этим частям и просуммировать.

Пример 1.4. Вычислить

∫∫(x2 + z)dσ,

где

z =1− x

σ - часть поверхности параболического цилиндра

z =1− x2 ,

ограниченная

плоскостями

y = 0,

z = 0, y = x.

Решение.

Рассматриваемая

часть

поверхности σ изображена на рис. 1.17. Область

D , проекция σ на плоскость Oxy , заштрихована.

z′x = −2x,

z′y = 0.

Следовательно,

dσ =

1+ 4x2 dxdy .

Тогда

соответствии

Рис. 1.17

формулой (1.15) получаем

∫∫(x2 + z)dσ = ∫∫(x2 +1− x2 )

1+ 4x2 dxdy =

= ∫dx∫ 1

+4x2 dy =

∫dx 1

+4x2 y

= ∫x 1+4x2 dx =

=	1	1	+4x2 d (1+4x2 )=	2	(1+4x2 )	3	2	1

		∫ 1
	8			8 3
		0						0

= 5 5 −1. 12

Решение задач

Задача 1.6. Найти дифференциал площади поверхности σ, задаваемой уравнением z = 3x − y +5.

Решение. Воспользуемся формулой	(1.16), учитывая, что
z′x = 3, z′y = −1. Тогда
dσ = 1+32 + (−1)2 dxdy =	11 dxdy .

Задача 1.7. Вычислить ∫∫(x2 + y2 − z2 +3)dσ, где σ - часть конуса

x + y = 2 z

x2 + y2 = z2 , лежащая между плоскостями

z = 2 и z = 0 .

Решение. Рассматриваемая часть конуса изображена на рис. 1.18. Область D , проекция σ на плоскость Oxy - круг радиусом 2 с

центром в точке O .

Для вычисления dσ выразим z из

уравнения поверхности и

найдем

z′x и z′y .

z = ± x2 + y2 .

Для рассматриваемой части

поверхности z ≥ 0 , значит

Рис. 1.18

z′x

; z′y

2 x2 + y2

x2 + y2

Тогда dσ =

dxdy =

2dxdy .

x2 + y2

+ y2

Теперь воспользуемся формулой (1.15), подставив в подынтегральную функцию вместо z выражение x2 + y2 . Получаем

∫∫(x2 + y2 − z2 +3)dσ = ∫∫(x2 + y2 −(x2 + y2 )+3)		2dxdy = 3 2∫∫dxdy .
σ	D	D

Полученный двойной интеграл ∫∫ dxdy равен площади круга радиусом 2, т.е.

π 22 = 4π. Следовательно,

∫∫(x2 + y2 − z2 +3)dσ = 3 2 4π =12 2π.

Задача 1.8. Вычислить ∫∫z2dσ, где σ - часть

сферы x2 + y2 + z2 =1, лежащая в первом

октанте (рис.1.19).

Решение. Выразим из уравнения сферы z , учитывая, что z ≥ 0 , и найдем dσ:

z =	1− x2	− y2	; z′x =	−x
				1− x2 − y2

1	x2	+ y2 + z2	=1

x	Рис. 1.19
1
, z′y =	−y	.
	1− x2 − y2

dσ =	1+	x2	+		y2	dxdy =	dxdy
								.
		1− x2 − y2			1− x2 − y2		1− x2 − y2
Тогда ∫∫z2dσ = ∫∫(1− x2 − y2 )					dxdy	= ∫∫ 1− x2 − y2 dxdy .
				1− x2 − y2
σ	D					D

Область D представляет собой четверть круга радиусом 1 с центром в начале координат. Для вычисления полученного двойного интеграла перейдем к полярным координатам и расставим пределы интегрирования, используя вид области D .

		π	1
			1
∫∫	1− x2 − y2 dxdy = ∫∫	1−ρ2 ρdρ = ∫2 dϕ∫ 1−ρ2 ρdρ =
D	D	0 0

		π∫2 dϕ∫1		(1−ρ2 )12 d (−ρ2	+1)= −			2 (1−ρ2 )32	1			π(0 −1)=	π.
= −	1					1	π∫2 dϕ	2 (1−ρ2 )32	1	= −	1
= −	2					2	π∫2 dϕ	3		= −	3
	2	0	0			2	0	3			3	2	6
		0	0				0
									0
									0

Задача 1.9. Найти массу части поверхности

σ: z2 − y2 =1,	задаваемой				неравенствами
x ≤ y ≤1, x ≥ 0,	z ≥ 0 ,		если					плотность
поверхности μ(x, y, z)=				1				.
поверхности μ(x, y, z)=			z2 + y2					.
Решение.	Воспользуемся							формулой
(1.14):				1
m = ∫∫μ(x, y, z)dσ = ∫∫				1			dσ.
m = ∫∫μ(x, y, z)dσ = ∫∫		z	2	+ y		2	dσ.
σ	σ	z		+ y

z	z2 − y2 =1
1

y = x

1 y

Рис. 1.20

Заданная поверхность – это гиперболический цилиндр. Его рассматриваемая часть изображена на рис. 1.20. Область D , проекция на плоскость Oxy заштрихована. Перейдем от поверхностного интеграла к

двойному, вычислив предварительно dσ. Выразим z из уравнения поверхности:

z = 1+ y2 ; z′x = 0, z′y =				y		;

				1+ y2
dσ = 1+	y2	dxdy =	1+ 2 y2		dxdy.
	+ y2		1+ y2
1

Тогда m = ∫∫			1					1+ 2 y2		dxdy = ∫∫					dxdy			.
Тогда m = ∫∫								1+ y2		dxdy = ∫∫								.
D 1+ y2 + y2								1+ y2						D 1+ y		2
Для области D			0 ≤ y ≤1,				а	0 ≤ x ≤ y. Следовательно,														(
1		y		dx			1	dy				y	1		ydy					1	1 d		y2	+1
												y

m = ∫dy∫						= ∫					x		= ∫				=				∫				)	=
m = ∫dy∫				1+ y	2	= ∫		1+ y	2		x		= ∫		2		=			2	∫	1+ y			2	=
0		0		1+ y			0	1+ y				0	0		1+ y						0	1+ y
0		0					0					0	0								0
=	1	∫1 (1+ y2 )−12 d (y2 +1)=											1	(1+ y2 )12 2					1 = 2 −1.
	1												1
	2												2
		0																	0
		0																	0

Вопросы для самопроверки по теме 1.2

1.Дайте определение поверхностного интеграла первого рода.

2.Перечислите свойства поверхностного интеграла первого рода.

3.Какой механический смысл имеет поверхностный интеграл первого рода?

4.Что такое дифференциал площади поверхности?

5.Сформулируйте теорему существования поверхностного интеграла первого рода.

6.Напишите формулу перехода от поверхностного интеграла первого рода к

двойному, если поверхность задается уравнением z = z(x, y).

1.3. Поверхностные интегралы второго рода

При изучении данной темы Вам предстоит ознакомиться со следующими вопросами:

•Сторона поверхности. Односторонние и двусторонние поверхности.

•Определение поверхностного интеграла второго рода и его основные свойства.

•Вычисление поверхностных интегралов второго рода.

•Формула Остроградского-Гаусса.

•Формула Стокса.

После изучения данных вопросов в опорном конспекте Вам следует

ответить на вопросы для самопроверки. Если Вы будете испытывать затруднения в ответах, обратитесь к [2] или к глоссарию. Студенты очнозаочной и заочной форм обучения должны решить задачу под № 101-110 из контрольной работы № 7 в соответствии со своим вариантом.

Рис. 1.21

Сторона поверхности. Односторонние и двусторонние поверхности

Понятие поверхностного интеграла второго рода строится по образцу криволинейного интеграла второго рода.

При определении криволинейного интеграла второго рода существенную роль играло направление кривой по которой идет интегрирование. Аналогом направления для поверхности будет служить понятие стороны поверхности. В ряде случаев это понятие интуитивно ясно (верхняя и нижняя стороны, внутренняя и внешняя). Исходя из таких интуитивных представлений, дадим точное определение стороны поверхности.

	Рассмотрим гладкую поверхность σ,
	зафиксируем на ней произвольную точку М.
M	Проведем через точку М нормаль к поверхности σ
M	и выберем на этой нормали одно определенное
σ	направление. Рассмотрим на поверхности σ

Lпроизвольный замкнутый контур L, проходящий через точку М и не пересекающий границы

поверхности σ. Будем перемещать точку М по выбранному контуру. При этом, так как поверхность σ - гладкая, то положение нормали меняется непрерывно. В каждом из ее

последовательных положений будем приписывать нормали то из двух направлений, в которое непрерывно переходит выбранное вначале направление. При возвращении точки М в исходное положение может

случиться одно из двух: либо мы вернемся в точку М с тем же направлением нормали, которое было вначале, либо - с противоположным ему.

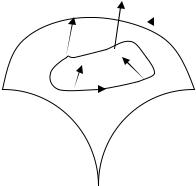
Если на гладкой поверхности σ существует хотя бы одна точка и хотя бы один замкнутый, не пересекающий границы поверхности контур, при обходе по которому направление нормали изменится на противоположное, то поверхность σ называется односторонней. Если для любой точки поверхности σ и любого замкнутого контура, не пересекающего границы поверхности σ, окажется, что после его обхода направление нормали не изменится, то поверхность называется двусторонней. Поверхность такого типа изображена на рис. 1.21.

Для двусторонней поверхности выбор направления нормали в одной точке однозначно определяет выбор направления нормали во всех точках поверхности. Назовем стороной двусторонней поверхности совокупность ее точек вместе с приписанными нормалями в них, непрерывно переходящими друг в друга.

Примерами двусторонних поверхностей могут служить плоскость, сфера, эллипсоид, параболоид, гиперболоид. Если поверхность задается уравнением z = z(x, y) и функции z(x, y), z′x (x, y), z′y (x, y) непрерывны, то эта поверхность также будет двусторонней.

	Классическим примером односторонней поверхности является лист (или
лента) Мебиуса . Ее модель						A		C
можно получить,				если
прямоугольный				кусок		B		D
бумаги ABCD (рис.1.22)
перекрутить		один		раз	и
склеить так, чтобы точка А
совпала с точкой С, а В - с
D.	Если	лист	Мебиуса			B D	B D
начать красить краской, то

можно, не переходя через						A C	A	C
его	границы,		закрасить
полностью весь лист одним							Рис. 1.22

цветом.
	Далее мы будем рассматривать только двусторонние поверхности.
	Направление обхода контура							σ ограничена
	Пусть	незамкнутая			гладкая двусторонняя		поверхность

контуром L, не имеющим точек самопересечения. Выберем определенную сторону этой поверхности. Если наблюдатель, находящийся на выбранной стороне поверхности, при движении по контуру видит саму поверхность слева,

то это направление будем называть положительным направлением обхода контура. Направление обхода, обратное положительному, называется отрицательным. Задание положительного направления однозначно определяет сторону поверхности, и наоборот. Аналогично определяется положительное направление обхода любого замкнутого без точек самопересечения контура, лежащего на поверхности σ. На рис. 1.21 показано положительное направление

обхода контура L.

Определение поверхностного интеграла второго рода и его основные свойства

Пусть σ - двусторонняя поверхность. Зафиксируем одну из ее двух сторон (т.е. зададим направление нормали). Пусть далее в точках поверхности

σопределена функция F(M ) = F(x, y, z) . Проделаем следующие операции:

1.Разобьем поверхность σ сетью произвольных кусочно-гладких кривых на п частей σ1, σ2 ,..., σn . Обозначим через λ1, λ2 ,..., λn

диаметры этих частей, а наибольший из этих диаметров обозначим через λ.

2.	В каждой области σi (i =1, 2,..., n)	выберем произвольно по точке
Mi (xi , yi , zi ) и вычислим F(xi , yi , zi ) .
3.	Спроектируем области σ1, σ2 ,...,	σn на координатную плоскость

А.Мёбиус (1790-1868) - немецкий математик.

Оху. Обозначим через	Si( xy) (i =1, 2,..., n) площадь проекции σi , взятую со
знаком плюс, если нормаль в точке Mi образует острый угол с осью Oz, и
площадь проекции σi ,	взятую со знаком минус, если нормаль в точке Mi

образует тупой угол с осью Oz. Если нормаль образует прямой угол с осью Oz,

то будем считать	Si( xy) равным нулю.
4. Найдем	сумму	n		, y , z )		S( xy)	,	которая	называется
		∑F(x
		i		i	i	i
		i =1	F(x, y, z) по						x и y по
интегральной суммой для		функции						переменным

выбранной стороне поверхности σ.

5. Вычислим lim ∑F(xi , yi , zi ) Si( xy) .

λ→0 i=1

Если этот предел существует, конечен и не зависит от способа разбиения поверхности σ на части и выбора точек Mi , то он называется поверхностным

интегралом второго рода по выбранной стороне поверхности σ от функцииF(x, y, z) по переменным x и y . Этот интеграл обозначают

символом ∫∫F(x, y, z)dxdy ,	при этом рассматриваемая сторона поверхности
σ
указывается особо. Таким образом, можно написать
	n
∫∫F(x, y, z)dxdy = lim ∑F(xi , yi , zi ) Si( xy) .
σ	λ→0 i=1

Если вместо плоскости Оху проектировать элементы поверхности σi на плоскость Oyz или Oxz, то аналогичным образом получим два других поверхностных интеграла второго рода:

∫∫F(x, y, z)dydz = lim		n	Si( yz) ,
		∑F(xi , yi , zi )
σ	λ→0 i=1
∫∫F(x, y, z)dxdz = lim		n	Si( xz) .
		∑F(xi , yi , zi )
σ	λ→0 i=1
Если в точках	поверхности σ	определены три функции P(

Q(x, y, z) , R(x, y, z) , то можно рассмотреть поверхностный интеграл

рода общего вида:

∫∫P(x, y, z)dydz +Q(x, y, z)dxdz + R(x, y, z)dxdy ,

(1.17)

(1.18)

x, y, z) ,

второго

определяемый равенством:
∫∫Pdydz +Qdxdz + Rdxdy = ∫∫Pdydz +∫∫Qdxdz + ∫∫Rdxdy.					(1.19)
σ	σ	σ	σ	σ
Напомним, что во всех	случаях	сторона	поверхности	σ	задается

отдельно.

Теорема 1.6. (Достаточные условия существования поверхностного интеграла второго рода). Если поверхность σ может быть задана уравнением z = z(x, y), где функция z(x, y) непрерывна в замкнутой и ограниченной

области D , являющейся проекцией поверхности σ на плоскости Oxy , а функция F(x, y, z) непрерывна на поверхности σ, то интеграл ∫∫F(x, y, z)dxdy существует.

Аналогичные теоремы можно сформулировать и для интегралов (1.17) и (1.18).

Основные свойства поверхностных интегралов второго рода

Перечислим простейшие свойства интегралов второго рода на примере интеграла ∫∫F(x, y, z)dxdy . При этом будем предполагать, что все

встречающиеся ниже функции и поверхности удовлетворяют условиям теоремы существования.

1. При перемене стороны поверхности интеграл ∫∫F(x, y, z)dxdy меняет знак.

		σ
2.	∫∫kF(x, y, z)dxdy = k ∫∫F(x, y, z)dxdy .
	σ	σ
3.	∫∫[F1(x, y, z) + F2 (x, y, z)]dxdy = ∫∫F1(x, y, z)dxdy +∫∫F2 (x, y, z)dxdy .
	σ	σ	σ
		Из свойств 2 и 3 следует свойство линейности:
∫∫[k1F1(x, y, z) + k2 F2 (x, y, z)]dxdy = k1 ∫∫F1(x, y, z)dxdy + k2 ∫∫F2 (x, y, z)dxdy.
σ		σ	σ

4. Свойство аддитивности.

Если поверхность σ разбита на две части σ1 и σ2 , то

∫∫F(x, y, z)dxdy = ∫∫F(x, y, z)dxdy + ∫∫ F(x, y, z)dxdy .

σ1

σ2

5. Если σ - цилиндрическая поверхность с образующими, параллельными оси

Oz , то

∫∫F(x, y, z)dxdy = 0 .

Связь между поверхностными интегралами первого и второго родов

Пусть σ - гладкая двусторонняя поверхность, на которой выбрана определенная сторона. Пусть также в точках поверхности σ определены

непрерывные	функции P(x, y, z),	Q(x, y, z),	R(x, y, z) .	Пусть далее
cos α, cosβ,	cos γ - направляющие	косинусы	нормали к	поверхности σ,

направленной в соответствии с выбранной стороной поверхности. Тогда справедлива формула:

∫∫Pdydz +Qdzdx + Rdzdy =∫∫(P cos α +Q cosβ+ R cos γ)dσ.							(1.20)
σ	σ
Замечание. Напомним, что, если поверхность σ задается уравнением
z = z(x, y), где функция z(x, y)		и ее частные	производные z′x (x, y) и
z′y (x, y) непрерывны в некоторой		области D, то	направляющие косинусы
нормали можно найти по формулам:		±z′x
cos α =		±z′x			,
cos α =		1+(z′x )2 +(z′y )2			,
cosβ =		±z′y				,	(1.21)
cosβ =		1+(z′x )2 +(z′y )2				,	(1.21)
cos γ =		1		.
cos γ =		1+(z′x )2 +(z′y )2		.

Знаки выбираются в зависимости от задаваемой стороны поверхности.

Вычисление поверхностных интегралов второго рода

1. Если σ - цилиндрическая поверхность с образующими, параллельными оси Oz , то

	∫∫R(x, y, z)dxdy = 0.	(1.22)
Если σ	σ
	- цилиндрическая поверхность с образующими, параллельными
оси Ох, то	∫∫P(x, y, z)dydz = 0 .	(1.23)

Если σ	σ
	- цилиндрическая поверхность с образующими, параллельными
оси Oy , то	∫∫Q(x, y, z)dxdz = 0.
		(1.24)
	σ

2. В общем случае вычисление поверхностных интегралов второго рода сводится к вычислению двойных интегралов. Приведем без доказательства формулы перехода к двойным интегралам.

Пусть поверхность	σ задается уравнением z = z(x, y), где	z(x, y) -
функция непрерывная в замкнутой ограниченной области D (D - проекция σ
на плоскость Оху). Тогда
∫∫R(x, y, z)dxdy = ∫∫R (x, y, z (x, y))dxdy ,		(1.25)
σ	D

если интегрирование идет по "верхней" стороне поверхности σ (т.е. нормаль к

поверхности образует острый угол с осью Oz).

∫∫R(x, y, z)dxdy = −∫∫R (x, y, z (x, y))dxdy ,										(1.26)
σ				D						σ (нормаль
если интегрирование идет по "нижней" стороне поверхности
образует тупой угол с осью Oz).									x = x (y, z),	где x (y, z) -
3. Если поверхность σ задается уравнением
функция непрерывная в замкнутой ограниченной области G (G - проекция σ
на плоскость Oyz), то			∫∫			(			)
∫∫	P(x, y, z)dydz	=		P
σ			G				x (y, z), y, z dydz ,			(1.27)
если нормаль к поверхности σ (соответствующая выбранной стороне) образует
острый угол с осью Ох, и				∫∫			(		)
∫∫	P(x, y, z)dydz	= −			P
σ				G				x (y, z), y, z dydz,		(1.28)

если нормаль к поверхности σ образует тупой угол с осью Ох.
4. Если поверхность σ задается уравнением									y = y (x, z),	где y (x, z) -

функция непрерывная в замкнутой ограниченной области Т (Т - проекция σ на

плоскость Oxz), то

∫∫

(

)

∫∫

Q(x, y, z)dxdz =

x, y (x, z), z dxdz,

(1.29)

если нормаль к поверхности σ

(соответствующая выбранной стороне) образует

острый угол с осью Оу, и

∫∫

(

)

∫∫

Q(x, y, z)dxydz = −

x, y (x, z), z dxdz,

(1.30)

если нормаль к поверхности σ образует тупой угол с осью Оу.

В приведенных

выше

формулах

предполагается, что

функции

P(x, y, z), Q(x, y, z),

R(x, y, z)

непрерывны на поверхности σ.

Пример 1.5. Вычислить ∫∫(x3 + z)dydz + x (y2 + z)dxdz +(4 − z)dxdy

по верхней стороне поверхности σ, где σ - часть параболического цилиндра z = 4 − y2 , лежащая в первом октанте между плоскостями x = 0 и y = 2x .

Решение. В соответствии с определением имеем:
∫∫(x3 + z)dydz + x (y2 + z)dxdz +(4 − z)dxdy =
σ
= ∫∫(x3 + z)dydz + ∫∫ x (y2 + z)dxdz +∫∫(4 − z)dxdy .
σ	σ	σ

Вычислим отдельно каждый из этих интегралов.

1) Так как σ - параболический цилиндр с образующими параллельными оси Ox , то в соответствии с формулой (1.23)

∫∫(x3 + z)dydz = 0 .

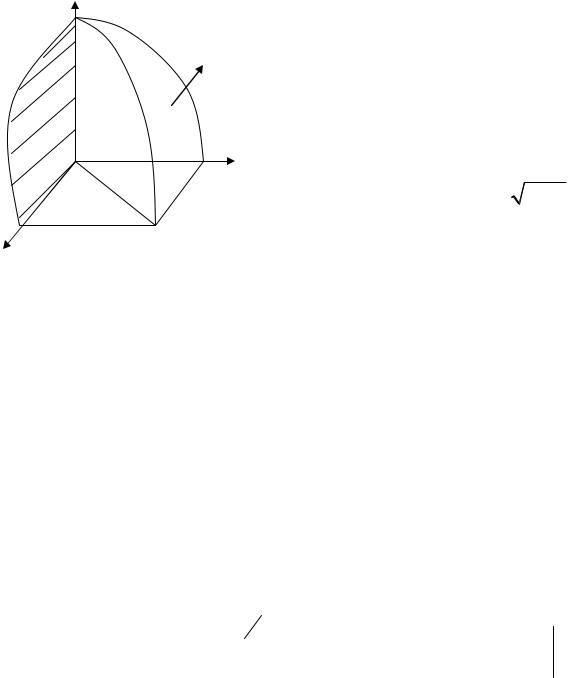
2) Так как нормаль к поверхности образует острый угол с осью Oy , то

при вычислении второго интеграла, интеграла по переменным x и z , будем использовать формулу (1.29). Спроектируем поверхность σ на плоскость Oxz (на рис. 1.23 проекция σ на плоскость Oxz заштрихована). Как видно из рис.

1.23, эта проекция Т ограничена осями координат и некоторой кривой,

	A	z = 4 − y2
	A
			n
		O	2 y
			F
B 1		Рис. 1.23	C

проходящей через точки А и В. Определим вид этой кривой из системы уравнений

	− y	2
z = 4	− y	.
y = 2x

Исключая переменную у, получаем

уравнение кривой: z = 4 − 4x2 .
Теперь	выразим из		уравнения
поверхности	y :	y =	4 − z	и

подставим в подынтегральную функцию; перейдем к двойному интегралу и вычислим его.

		1	4−4 x2	1
∫∫ x (y2	+ z)dxdz = ∫∫ x (4 − z + z)dxdz = ∫dx		∫	4xdz = 4∫dx xz	04−4 x2 =
∫∫ x (y2	+ z)dxdz = ∫∫ x (4 − z + z)dxdz = ∫dx		∫	4xdz = 4∫dx xz	04−4 x2 =
σ	T	0	0	0

1	(		)		1		)	(		)		(		)		1
1					1											1
∫		2			∫(	2			2				2		2
=16 x 1− x		2	dx = −8 1− x			2		d 1− x	2		= −4 1− x		2		2	= 4.
=16 x 1− x			dx = −8 1− x					d 1− x			= −4 1− x					= 4.
0					0											0
0					0											0
3) Для вычисления третьего интеграла, интеграла по переменным x и y ,
будем использовать формулу (1.25) (нормаль образует острый угол с Oz ).
Подставляя в подынтегральную функцию z = 4 − y2 , получаем
				∫∫(4 − z)dxdy = ∫∫ y2dxdy,
				σ				D
где область D - это треугольник OCF .

Вычислим двойной интеграл. Тогда

		2	y	2		y		1	2	1

∫∫(4 − z)dxdy = ∫∫ y2dxdy = ∫dy ∫2				y2dx = ∫ y2dyx	2		=		∫ y3dy =		y4
								2		8
σ	D	0	0	0	0				0

Суммируя полученные результаты, окончательно получаем

∫∫(x3 + z)dydz + x(y2 + z)dxdy +(4 − z)dxdy = 0 +4 + 2 = 6.

= 2.

Формула Остроградского-Гаусса

В теории криволинейных интегралов мы познакомились с формулой Грина - формулой, связывающей двойной интеграл по плоской области с криволинейным интегралом по границе этой области. Ее аналогом в теории поверхностных интегралов является формула Остроградского-Гаусса, которая связывает тройной интеграл по пространственной области с поверхностным

интегралом по поверхности, ограничивающей эту область.

σ. Если в

Пусть

тело T

ограничено кусочно-гладкой

поверхностью

области

определены

три функции P(x, y, z) , Q(x, y, z) и

R(x, y, z) ,

непрерывные вместе со своими частными производными

∂P

, ∂Q

и ∂R

, то

∂x

∂y

∂z

справедлива формула

∫∫Pdydz +Qdxdz + Rdxdy =

∂P

+ ∂Q

∂R

(1.31)

∫∫∫

dxdydz.

∂x

∂y

∂z

Эта формула называется формулой Остроградского-Гаусса.

Пример

1.6.

Вычислить,

используя

формулу

Остроградского-Гаусса,

интеграл

∫∫(x + y)dydz +(y + z)dxdz +(z + x)dxdy , где

σ - внешняя сторона поверхности треугольной

пирамиды,

образованной

координатными

y плоскостями

x = 0, y = 0,

z = 0 и плоскостью

x + y + z = 2. (рис. 1.24).

P = x + y,

Решение. В нашем случае

Рис. 1.24

Q = y + z, R = z + x ,

и,

следовательно,

по

формуле (1.31) получаем

∫∫(x + y)dydz +(y + z)dxdz +(z + x)dxdy = ∫∫∫3dxdydz = 3∫∫∫dxdydz .

Здесь

треугольная

пирамида,

образованная

указанными

в условии

плоскостями. Вспомним свойство тройного интеграла: ∫∫∫dxdydz равен объему

тела Т, т.е. объему пирамиды АОСВ. Объем пирамиды равен одной трети площади основания на высоту, т.е.

3	dxdydz = 3	1		1	AO OC OB = 3	4	= 4.

∫∫∫	3		2		3
T

М.В.Остроградский (1801-1861) - русский математик; К.Гаусс (1777-1855) - немецкий математик.

Формула Стокса

Формула Стокса является обобщением формулы Грина и связывает поверхностный интеграл с криволинейным.

Пусть

гладкая

двусторонняя

поверхность,

ограниченная кусочно-гладким

контуром L (рис. 1.25).

Выберем на

поверхности

определенную

сторону.

Как

было

установлено

ранее,

выбор

стороны

поверхности

определяет

положительное

направление

обхода

контура

L .

Пусть

на

поверхности

σ ,

включая

контур

L ,

заданы

непрерывные

функции

Рис. 1.25

P(x, y, z) ,

Q(x, y, z) ,

R(x, y, z) ,

имеющие

непрерывные частные производные. Тогда имеет место равенство:

∫

Pdx +Qdy +Rdz =

∂Q

−

∂P dxdy +

∂R −

∂Q dydz

+ ∂P −

∂R dxdz . (1.32)

∫∫

∂x

∂y

∂z

∂x

Это равенство называется формулой Стокса. В этой формуле выбор стороны поверхности должен соответствовать положительному направлению

обхода контура.

Замечание. Если в качестве поверхности σ взять плоскую область D на координатной плоскости Oxy(z = 0) , то в правой части (1.32) останется только

первое слагаемое, и получится формула ∫ Pdx +Qdy =∫∫		∂Q	−	∂P	dxdy , т.е.
L	D	∂x		∂y

формула Грина. Таким образом, формула Грина является частным случаем формулы Стокса.

Пример 1.7. Используя формулу Стокса, вычислить интеграл

∫ xdx +(y2 + z2 )dy − z2dz ,

где L - линия пересечения части поверхности конуса x2 + z2 = (y − 2)2

лежащей в первом октанте, с координатными плоскостями, а направление обхода контура показано на рис. 1.26.

Дж.CTOKC (1819-1903) английский математик и физик. 43

Решение. В нашем случае P = x, Q = y2 + z2 , R = −z2 . Вычислим частные производные, входящие в формулу (1.32):

∂Q −

∂P

= 0 −0 = 0,

∂R

− ∂Q

= 0 − 2z = −2z,

∂P − ∂R = 0

−0 = 0.

∂x

∂y

∂z

∂x

Заданному направлению обхода контура соответствует верхняя сторона

поверхности

σ. Следовательно, по формуле Стокса (1.32) получаем

∫ xdx +(y2 + z2 )dy − z2dz = ∫∫(−2z)dydz.

Перейдем

от

поверхностного

интеграла

двойному,

спроектировав

поверхность

на

плоскость

Oyz

(проекция

на

Oyz

на

рис. 1.26

заштрихована).

Уравнение

прямой,

x 2

Рис. 1.26

ограничивающей

область

сверху,

получим из уравнения конуса,

положив в

нем

x = 0 :

= (y − 2)2

или

z = ±(y − 2). Так как в области D

z < 2 , то искомое уравнение

z = 2 − y .

Тогда

∫∫(−2z)dydz = ∫∫(−2z)dydz = −2∫dy

∫

zdz = −∫(2 − y)2 dy = −(y −

= −8.

2−y

Решение задач

Задача 1.10. Перейти от поверхностного интеграла второго рода ∫∫ xdydz + ydxdz + zdxdy (формула (1.10)) по верхней стороне части плоскости

σ	+ y + z =1, заключенной между координатными плоскостями, к
x

поверхностному интегралу первого рода и вычислить его. Решение. Рассматриваемая часть

поверхности изображена на рис.1.27.

Воспользуемся формулой (1.20), вычислив
предварительно		косинусы	соответствующих
углов по формулам (1.21). Уравнение плоскости
σ запишем в		виде	z = −x − y .	Тогда
z′x = −1;	z′y = −1.	Учитывая, что для		верхней
стороны	плоскости		косинусы	углов
положительны, получаем				x 1
			44

1 σ

O y

Рис.1.27

cos α =	1	; cosβ =	1	; cos γ =				1		.
			3					3
3
Подставляем в формулу (1.20):				x		y			z

∫∫ xdydz + ydxdz + zdxdy =			∫∫		+		+				dσ.
				3		3		3
σ			σ

Для вычисления полученного интеграла первого рода используем формулу

(1.15), при этом dσ =

1+(−1)2 +(−1)2 dxdy = 3dxdy . Тогда

1− x − y

∫∫

dσ =

∫∫

3dxdy = ∫∫dxdy.

Область D (на рис. 1.27 заштрихована) – это треугольник с катетами равными единице, а полученный интеграл равен площади области D . Значит,

∫∫dxdy =	1	1 1 =	1	.
	2		2
D

1 y

x 1 x2 + z2 = y2

Рис. 1.28

Задача 1.11. Вычислите ∫∫4ey2 dxdz , где

σ - внешняя		σ
σ - внешняя	часть поверхности конуса
x2 + z2 = y2 ,	ограниченная	плоскостями

x = 0, z = 0, y = 0 и y =1 (x ≥ 0, z ≥ 0).

Решение. Рассматриваемая часть поверхности конуса изображена на рис. 1.28. Ее проекция D на плоскость Oxz - это четверть круга радиусом 1 с центром в начале координат (на рис. 1.28 заштрихована).

Так как нормаль к поверхности образует тупой угол с осью Oy , то воспользуемся формулой

	(1.30). При этом y2 заменим на x2 + z2 . Тогда
∫∫4ey2 dxdz = −4∫∫ex2 +z2 dxdz .
σ	D

Для вычисления двойного интеграла перейдем к полярным координатам:

				π	1	1	π	1
					1			1
−4∫∫ex2 +z2 dxdz = −4∫∫eρ2 ρdϕdρ = −4 ∫2 dϕ∫eρ2 ρdρ = −4							∫2 dϕ∫eρ2 dρ2 =
D	D			0	0	2	0 0
	= −2 ϕ	0π2 eρ2	1 = −2	π	(e −e0 )= π(1−e).


			0	2
			0	2

Задача 1.12.	Вычислите	∫∫(2z + x2 )dydz + xyzdxdy , где		σ	- часть
		σ
гиперболического	цилиндра	x2 − y2 =1, ограниченная		плоскостями
y = 0, z = 0 и y + z = 2 (x ≥ 0, y ≥ 0). Нормаль к			поверхности		образует
острый угол с осью Oy .
Решение. В соответствии с определением имеем:
∫∫(2z + x2 )dydz + xyzdxdy = ∫∫(2z + x2 )dydz + ∫∫ xyzdxdy .
σ		σ	σ

Вычислим отдельно каждый из этих интегралов.

1) Так как σ - цилиндр с образующими, параллельными оси Oz , то по формуле (1.22) получаем ∫∫ xyzdxdy = 0.

2) Рассматриваемая часть поверхности изображена на рис. 1.29,а. Так как

x2 − y2 =1	z	z
	2
		2	y + z = 2

x	O	O	2	y
	2
y а)			б)
		Рис.1.29

нормаль к поверхности образует острый угол с осью Oy , то для вычисления

интеграла по переменным x и z будем использовать формулу (1.29). Проекция D поверхности на плоскость Oyz изображена на рис. 1.29,б. Переменную x

выразим из уравнения поверхности σ: x2 =1+ y2 . Тогда

∫∫(	2z + x2			)	dydz =		∫∫(		2z +1+ y2										)	dydz =					2 dy2−y			(	2z +1+ y2 dz =
∫∫(				)			∫∫(												)						∫		∫	(					)
σ							D																		0		0
		2		2	+ z + y		2	z)				2−y		2				2 − y)					2	+ 2 − y + 2 y						2	− y		3
												2−y

=		∫dy (z												= ∫		(																	dy =
		0	(2 − y)			3						0	2	0			3					4		2
		0										0		0
										y					y						y					8						16

=		−				+ 2 y		−						+ 2					−						=		+ 4 −2			+			−4 = 6.
=		−	3			+ 2 y		−						+ 2					−						=	3	+ 4 −2			+			−4 = 6.
			3								2					3				4						3					3
																		46						0
																								0

Задача

1.13.

Используя теорему

+ y

Остроградского-Гаусса,

вычислить

∫∫2xzdydz −(x2 + z2 )dxdz + xydxdy , где

σ - внешняя сторона полной поверхности

тела, ограниченного

частью

эллипсоида

x2 + y2 +

=1 при

z ≥ 0 и плоскостью

z = 0 .

Решение. В нашем случае

Рис.1.30

P = 2xz, Q = −(x

+ z

), R

= xy . Тогда

∂P

= 2z, ∂Q = 0,

∂R = 0.

∂x

∂y

∂z

Используя формулу (1.31), получаем

∫∫2xzdydz −(x2 + z2 )dxdz + xydxdy = ∫∫∫2zdxdydz.

Область T изображена на рис. 1.30. Для вычисления полученного тройного интеграла перейдем к цилиндрическим координатам.

1−ρ

2zdz = ∫∫ρdϕdρz2

1−ρ2

∫∫∫2zdxdydz = ∫∫∫2zρdϕdρdz = ∫∫ρdϕdρ

∫

= 4∫∫(1−ρ2 )ρdρdϕ = 42∫π dϕ∫1 (1−ρ2 )ρdρ =

= −22∫π dϕ∫1 (1−ρ2 )d (1−ρ2 )= −2 ϕ

2π (1−ρ2 )2

1 = 2π.

Задача

1.14.

Используя

формулу

Стокса,

вычислить

∫ x3dx −(y2 +5)dy +

(x3 − 2)dz , где L - линия пересечения части плоскости

+ y + 2z = 2,

лежащей в первом октанте с координатными плоскостями, а

направление обхода контура идет от оси Ox к оси Oy и к оси Oz .

Решение.

нашем случае

P = x3 ,

Q = −(y2 +5),

R = x3 − 2 .

Вычислим частные производные, входящие в формулу Стокса (1.32):

∂∂Qx − ∂∂Py = 0, ∂∂Ry − ∂∂Qz = 0, ∂∂Pz − ∂∂Rx = −3x2 .

Заданному направлению обхода контура соответствует верхняя сторона плоскости (рис. 1.31). Тогда

<<< < Предыдущая 1 2 3 4 56 / 146 7 8 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.02.2016164.35 Кб6Маркетингт.doc
#
16.02.2016120.32 Кб13Мат.ч.1.doc
#
16.02.201646.08 Кб17Мат.ч.2.doc
#
16.02.2016772.83 Кб47Математика для 1 курса.pdf
#
18.11.20185.16 Mб26МАТЕМАТИКА методичка.doc
#
16.02.20162.14 Mб62Математика ч.1 (УМК 7,8).pdf
#
16.02.20161.56 Mб36Математика ч.2 (УМК).pdf
#
16.02.20162.03 Mб30Математика часть 1 УМК.pdf
#
16.02.201644.99 Кб22Математика(шифр 03).docx
#
16.02.20162.68 Mб40МатериаловедениеМУРЛ2007.doc
#
16.02.20165.56 Mб85МатериаловедениеУМК2008.doc