
- •Математика. Ч. 1
- •1. Информация о дисциплине
- •1.1. Предисловие
- •1.2. Содержание дисциплины и виды учебной работы
- •2. Рабочие учебные материалы
- •2.1. Рабочая программа
- •2.2. Тематический план дисциплины
- •2.4. Временной график изучения дисциплины
- •2.5. Практический блок
- •3. Информационные ресурсы дисциплины
- •3.1. Библиографический список
- •3.2. Опорный конспект
- •Раздел 1. Тройные и поверхностные интегралы
- •Раздел 2. Теория поля
- •Раздел 3. Ряды Фурье
- •Раздел 4. Уравнения математической физики
- •Заключение
- •3.3. Глоссарий
- •4. Блок контроля освоения дисциплины
- •4.2. Задания на контрольные работы № 7,8
- •4.3. Текущий контроль
- •4.4. Итоговый контроль
2.Рабочие учебные материалы
2.1.Рабочая программа (объем 146 часов)
Введение (2 часа)
[1], с.4...5; [5], с.3...4
Предмет и задачи дисциплины. Основные этапы развития математики. Ее роль в учебном процессе, научных исследованиях и промышленном производстве.
Раздел 1. Тройные и поверхностные интегралы (36 часов)
[2], с.9-15; [4], с.15; [5], с.16
1.1 Тройные интегралы Тройной интеграл, его физический смысл, свойства. Вычисления тройного
интеграла в декартовых координатах. Замена переменных в тройном интеграле; переход к цилиндрическим и сферическим координатам.
1.2. Поверхностные интегралы первого рода Поверхностный интеграл первого рода. Его физический смысл; свойства.
Вычисления поверхностных интегралов первого рода.
1.3. Поверхностные интегралы второго рода Поверхностный интеграл второго рода. Односторонние и двусторонние
поверхности, сторона поверхности. Его физический смысл, свойства. Вычисления поверхностных интегралов второго рода. Связь между поверхностными интегралами первого и второго рода. Формула Остроградского-Гаусса и формула Стокcа в координатной форме.
Раздел 2. Теория поля (40 часов)
[2], с.35-40; [4], с.10-15;[5], с.11, с.3-8; [7], с.10-13.
2.1. Скалярное поле Определение скалярного поля. Производная по направлению. Градиент
скалярного поля. Гармоническое скалярное поле.
2.2. Векторное поле. Поток и циркуляция векторного поля Определение векторного поля. Векторные линии, векторные поверхности,
векторные трубки. Поток векторного поля через поверхность, его непосредственные вычисления. Дивергенция векторного поля, формула Остроградского-Гаусса в векторной форме. Циркуляция векторного поля, ее вычисление. Ротор векторного поля, формула Стокса в векторной форме.
2.3. Потенциальные и соленоидальные векторные поля Потенциальное векторное поле; его свойства. Нахождение потенциала
векторного поля. Соленоидальное векторное поле, его свойства.
2.4. Векторно-дифференциальные операторы I и II порядков Векторно-дифференциальные операторы. Оператор Гамильтона. Оператор
Лапласа.
5
Раздел 3. Ряды Фурье (14 часов)
[1], с.10-15; [5], с.11, с.3-8; [8], с.10-13
3.1. Пространство функций со скалярным произведением. Ортогональная система функций
Пространство функций со скалярным произведением. Ортогональная система функций
3.2. Тригонометрические ряды Фурье Ряды Фурье по тригонометрическим системам. Разложение функций в
тригонометрические ряды Фурье. Условие поточечной сходимости «в среднем». Применение тригонометрических рядов Фурье в приближенных вычислениях.
3.3. Комплексная форма ряда Фурье Разложение функций в комплексный ряд Фурье. Условия разложимости.
Раздел 4. Уравнения математической физики (52 часа)
[3], с.9-55;[6], с.25; [8], с.18.
4.1. Вывод основных дифференциальных уравнений в частных производных 2-го порядка
Физические задачи, приводящие к дифференциальным уравнениям в частных производных. Вывод уравнений колебаний струны, теплопроводности
идиффузии. Электромагнитное поле, уравнения Максвелла.
4.2.Классификация дифференциальных уравнений в частных производных
2-го порядка. Краевые задачи Классификация линейных дифференциальных уравнений в частных
производных 2-го порядка. Постановка основных краевых задач: задача Коши, краевые задачи, смешанные задачи. Корректность постановки задач.
4.3. Уравнение Лапласа Уравнение Лапласа. Формула Грина. Гармоническая функция, теорема о
среднем значении, принцип максимума. Задача на собственные значения и собственные функции для оператора Лапласа.
4.4. Метод Фурье для решения волнового уравнения и уравнения теплопроводности
Метод Фурье решения смешанных задач для волнового уравнения и уравнения теплопроводности. Задача Штурма-Лиувилля, собственные функции и собственные значения.
4.5. Функции Бесселя Функция Бесселя. Основные свойства.
4.6. Интегральные уравнения. Их классификация, методы решения Классификация интегральных уравнений. Теоремы Фредгольма и
альтернатива Фредгольма. Метод последовательных приближений для решения интегральных уравнений. Проекционный метод, метод Галеркина.
6
4.7. Решение задачи Коши для волнового уравнения и уравнения теплопроводности. Обобщенные функции.
Решение задачи Коши для одномерного волнового уравнения методом Даламбера. Задача Коши для уравнения теплопроводности, интеграл Пуассона. Понятия обобщенных функций и обобщенных решений. Фундаментальное решение.
Заключение (2 часа)
Изложенный учебный материал служит основой для изучения не только последующих разделов математики, но и остальных технических дисциплин.
7

2.2.Тематический план дисциплины
2.2.1.Тематический план дисциплины
для студентов очной формы обучения
|
|
Количествочасов по формеочнойобучения |
|
Виды занятий и контроля |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
.Ауд |
ДОТ |
.Ауд |
|
ДОТ |
Самостоятельная работа |
теста№ |
№ПЗ |
|
|
|
|
Лекции |
|
ПЗ |
|
|
|
||
№ |
Название раздела, темы |
|
|
|
|
|
|
|
|
|
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВСЕГО |
146 |
44 |
|
24 |
|
20 |
58 |
|
|
|
1 |
Введение. Тройные и поверхностные |
38 |
|
|
|
|
|
16 |
1 |
|
|
интегралы |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1.1 |
Тройные интегралы |
|
4 |
|
2 |
|
2 |
|
|
1 |
1.2 |
Поверхностные интегралы первого рода |
|
4 |
|
2 |
|
2 |
|
|
2 |
1.3 |
Поверхностные интегралы второго рода |
|
2 |
|
2 |
|
2 |
|
|
3 |
2 |
Теория поля |
40 |
|
|
|
|
|
16 |
2 |
|
2.1 |
Скалярное поле |
|
4 |
|
2 |
|
2 |
|
|
4 |
2.2 |
Векторное поле. Поток и циркуляция |
|
4 |
|
4 |
|
|
|
|
5 |
|
векторного поля |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
2.3 |
Потенциальные и соленоидальные |
|
2 |
|
2 |
|
2 |
|
|
6 |
|
векторные поля |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
2.4 |
Векторно-дифференциальные операторы I и |
|
2 |
|
|
|
|
|
|
|
|
II порядков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
Ряды Фурье |
14 |
|
|
|
|
|
6 |
3 |
|
3.1 |
Пространство функций со скалярным |
|
2 |
|
|
|
|
|
|
|
|
произведением. Ортогональная система |
|
|
|
|
|
|
|
|
|
|
функций |
|
|
|
|
|
|
|
|
|
3.2 |
Тригонометрические ряды Фурье |
|
2 |
|
2 |
|
|
|
|
7 |
3.3 |
Комплексная форма ряда Фурье |
|
2 |
|
|
|
|
|
|
|
4 |
Уравнения математической физики |
54 |
|
|
|
|
|
20 |
4 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
4.1 |
Вывод основных дифференциальных |
|
|
|
|
|
|
|
|
|
|
уравнений в частных производных 2-го |
|
4 |
|
2 |
|
2 |
|
|
8 |
|
порядка |
|
|
|
|
|
|
|
|
|
4.2 |
Классификация дифференциальных |
|
|
|
|
|
|
|
|
|
|
уравнений в частных производных 2-го |
|
2 |
|
|
|
|
|
|
|
|
порядка. Краевые задачи |
|
|
|
|
|
|
|
|
|
4.3 |
Уравнение Лапласа |
|
2 |
|
|
|
|
|
|
|
4.4 |
Метод Фурье для решения волнового |
|
2 |
|
2 |
|
4 |
|
|
9 |
|
уравнения и уравнения теплопроводности |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
4.5 |
Функции Бесселя |
|
2 |
|
|
|
|
|
|
|
4.6 |
Интегральные уравнения. Их |
|
2 |
|
2 |
|
2 |
|
|
10 |
|
классификация, методы решения |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
4.7 |
Решение задачи Коши для волнового |
|
|
|
|
|
|
|
|
|
|
уравнения и уравнения теплопроводности. |
|
2 |
|
2 |
|
2 |
|
|
11 |
|
Обобщенные функции. Заключение |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
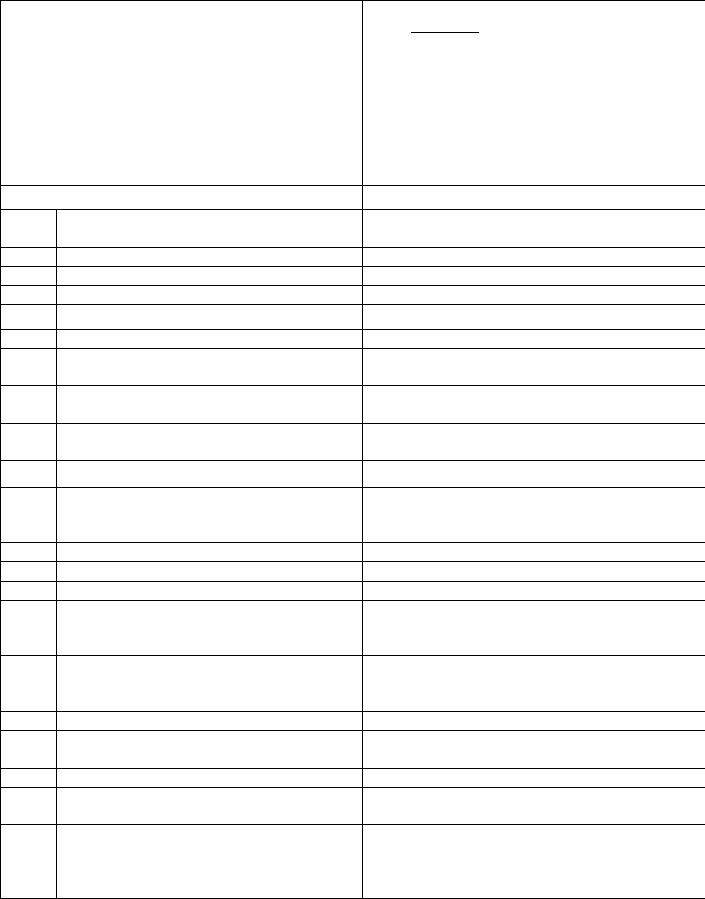
2.2.2. Тематический план дисциплины
для студентов очно-заочной формы обучения
|
|
|
часов по |
обучения |
№ п/п |
|
Название раздела, темы |
Количество |
очной форме |
|
|
|
||
|
|
|
|
|
ВСЕГО |
|
146 |
||
1 |
|
Введение. Тройные и поверхностные |
38 |
|
|
|
интегралы |
||
|
|
|
|
|
1.1Тройные интегралы
1.2Поверхностные интегралы первого рода
1.3Поверхностные интегралы второго рода
2 |
Теория поля |
40 |
2.1Скалярное поле
2.2Векторное поле. Поток и циркуляция векторного поля
2.3Потенциальные и соленоидальные векторные поля
2.4Векторно-дифференциальные операторы I и II порядков
3 |
Ряды Фурье |
14 |
3.1Пространство функций со скалярным произведением. Ортогональная система функций
3.2Тригонометрические ряды Фурье
3.3Комплексная форма ряда Фурье
4 |
Уравнения математической физики |
54 |
4.1Вывод основных дифференциальных уравнений в частных производных 2-го порядка
4.2Классификация дифференциальных уравнений в частных производных 2-го порядка. Краевые задачи
4.3Уравнение Лапласа
4.4Метод Фурье для решения волнового уравнения и уравнения теплопроводности
4.5Функции Бесселя
4.6Интегральные уравнения. Их классификация, методы решения
4.7Решение задачи Коши для волнового уравнения и уравнения теплопроводности. Обобщенные функции. Заключение
9
|
|
Виды занятий и контроля |
|
||||||
.Ауд |
ДОТ |
|
|
|
|
|
|
|
|
|
.Ауд |
|
ДОТ |
Самостоятельная работа |
теста№ |
№ПЗ |
контрольной№ работы |
||
лекции |
|
|
ПЗ |
|
|
|
|
||
12 |
32 |
|
24 |
|
20 |
58 |
|
|
|
|
|
|
|
|
|
16 |
1 |
|
7 |
2 |
2 |
|
2 |
|
2 |
|
|
1 |
|
|
4 |
|
2 |
|
2 |
|
|
2 |
|
|
2 |
|
2 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
16 |
2 |
|
8 |
2 |
2 |
|
2 |
|
2 |
|
|
4 |
|
|
4 |
|
4 |
|
|
|
|
5 |
|
|
2 |
|
2 |
|
2 |
|
|
6 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
3 |
|
7 |
|
2 |
|
|
|
|
|
|
|
|
2 |
2 |
|
2 |
|
|
|
|
7 |
|
|
|
|
|
|
20 |
4 |
|
7 |
|
|
|
|
|
|
|
|
|||
2 |
2 |
|
2 |
|
2 |
|
|
8 |
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
4 |
|
|
9 |
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
10 |
|
2 |
|
|
2 |
|
2 |
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|

2.2.3. Тематический план дисциплины
для студентов заочной формы обучения
|
|
Количествочасов по формеочнойобучения |
|
Виды занятий и контроля |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.Ауд |
ДОТ |
.Ауд |
|
ДОТ |
Самостоятельная работа |
теста№ |
№ПЗ |
контрольной№ работы |
|
|
|
|
Лекции |
|
ПЗ |
|
|
|
|
||
№ |
Название раздела, темы |
|
|
|
|
|
|
|
|
|
|
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВСЕГО |
146 |
6 |
38 |
8 |
|
36 |
58 |
|
|
|
|
1 |
Введение. Тройные и поверхностные |
38 |
|
|
|
|
|
16 |
1 |
|
7 |
|
интегралы |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1.1 |
Тройные интегралы |
|
2 |
2 |
|
|
4 |
|
|
1 |
|
1.2 |
Поверхностные интегралы первого рода |
|
|
4 |
2 |
|
2 |
|
|
2 |
|
1.3 |
Поверхностные интегралы второго рода |
|
|
2 |
|
|
4 |
|
|
3 |
|
2 |
Теория поля |
40 |
|
|
|
|
|
16 |
2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
2.1 |
Скалярное поле |
|
|
4 |
|
|
4 |
|
|
4 |
|
2.2 |
Векторное поле. Поток и циркуляция |
|
2 |
2 |
|
|
4 |
|
|
5 |
|
|
векторного поля |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2.3 |
Потенциальные и соленоидальные |
|
|
2 |
2 |
|
2 |
|
|
6 |
|
|
векторные поля |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2.4 |
Векторно-дифференциальные операторы I |
|
|
2 |
|
|
|
|
|
|
|
|
и II порядков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
Ряды Фурье |
14 |
|
|
|
|
|
6 |
3 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
3.1 |
Пространство функций со скалярным |
|
|
|
|
|
|
|
|
|
|
|
произведением. Ортогональная система |
|
|
2 |
|
|
|
|
|
|
|
|
функций |
|
|
|
|
|
|
|
|
|
|
3.2 |
Тригонометрические ряды Фурье |
|
|
2 |
2 |
|
|
|
|
7 |
|
3.3 |
Комплексная форма ряда Фурье |
|
|
2 |
|
|
|
|
|
|
|
4 |
Уравнения математической физики |
54 |
|
|
|
|
|
20 |
4 |
|
7 |
4.1 |
Вывод основных дифференциальных |
|
|
|
|
|
|
|
|
|
|
|
уравнений в частных производных 2-го |
|
2 |
2 |
|
|
4 |
|
|
8 |
|
|
порядка |
|
|
|
|
|
|
|
|
|
|
4.2 |
Классификация дифференциальных |
|
|
|
|
|
|
|
|
|
|
|
уравнений в частных производных 2-го |
|
|
2 |
|
|
|
|
|
|
|
|
порядка. Краевые задачи |
|
|
|
|
|
|
|
|
|
|
4.3 |
Уравнение Лапласа |
|
|
2 |
|
|
|
|
|
|
|
4.4 |
Метод Фурье для решения волнового |
|
|
2 |
2 |
|
4 |
|
|
9 |
|
|
уравнения и уравнения теплопроводности |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
4.5 |
Функции Бесселя |
|
|
2 |
|
|
|
|
|
|
|
4.6 |
Интегральные уравнения. Их |
|
|
2 |
|
|
4 |
|
|
10 |
|
|
классификация, методы решения |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
4.7 |
Решение задачи Коши для волнового |
|
|
|
|
|
|
|
|
|
|
|
уравнения и уравнения |
|
|
2 |
|
|
4 |
|
|
11 |
|
|
теплопроводности. Обобщенные |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
функции. Заключение |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
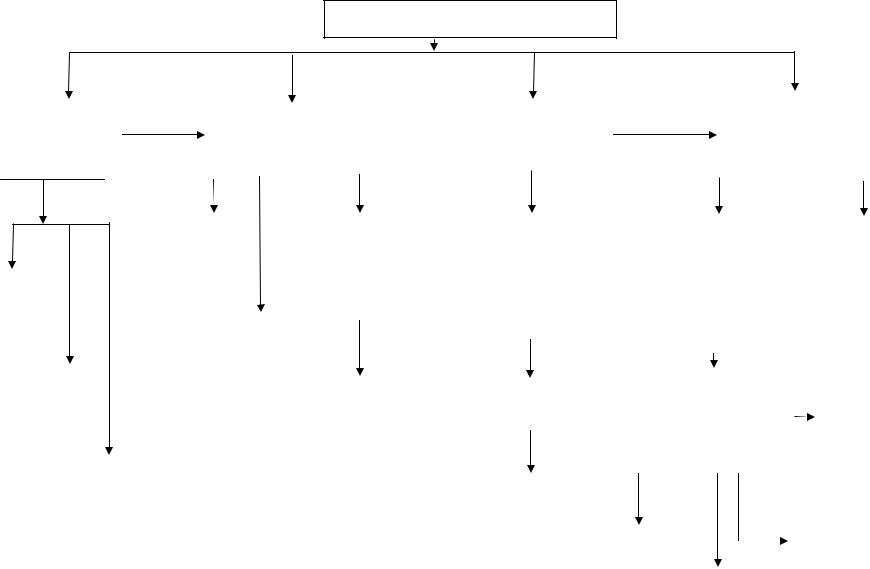
2.3. Структурно-логическая схема дисциплины «Математика, часть 1»
Математика, часть 1, 4-й семестр
Раздел 1. |
|
|
|
Раздел 2. |
|||
Тройные и |
|
||
|
Теория поля |
||
поверхностные |
|
||
|
|
||
интегралы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Скалярное поле |
|
|
|
Векторное |
|
|
|
|
|
|
|
|
|
|
|
|
поле. Поток и |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
циркуляция |
|
Тройные |
|
|
|
|
|
|
|
|
векторного |
|
|
интегралы |
|
|
|
|
|
|
|
|
поля |
|
|
|
|
|
|
|
Векторно- |
|
|
|
|
||
|
|
|
|
|
дифференциальные |
|
|
|
|
||
|
|
|
|
|
операторы I и II |
|
|
|
|
||
Поверхностные |
|
|
|
|
|
|
|||||
|
|
порядков |
|
|
|
|
|||||
|
|
|
|
Потенциальные и |
|
||||||
интегралы I |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
рода |
|
|
|
|
|
|
|
соленоидальные |
|
||
|
|
|
|
|
|
|
|
|
|
векторные поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
Поверхностные |
|
|
|
|
|
|
||||
|
|
интегралы II |
|
|
|
|
|
||||
|
|
|
рода |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Раздел 4. |
|
|
||||
|
|
|
Раздел 3. |
|
|
|
|
|
|
||||||
|
|
|
Ряды Фурье |
|
|
|
|
Уравнения |
|
|
|||||
|
|
|
|
|
|
|
|
|
математической |
|
|
||||
|
|
|
|
|
|
|
|
|
физики |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Пространство |
|
|
Классификация |
|
Интегральные |
|
||||||
|
|
|
функций со |
|
|
дифференциальных |
|
уравнения. |
|
||||||
|
|
|
скалярным |
|
|
уравнений в |
|
Их классификация, |
|
||||||
|
|
|
произведением. |
|
|
частных |
|
методы решения |
|
||||||
|
|
|
Ортогональная |
|
|
производных 2-го |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
система функций |
|
|
порядка. Краевые |
|
|
|
|
|||||
|
|
|
|
|
|
|
задачи |
|
|
|
|
||||
|
|
|
|
|
|
|
Метод Фурье для |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
решения |
|
|
|
|
|
|
|
|
|
Вывод основных |
|
|
||||||
|
|
|
|
|
|
|
|
волнового |
|
||||||
|
|
|
Тригонометрические |
|
|||||||||||
|
|
|
|
|
дифференциальных |
|
уравнения и |
|
|||||||
|
|
|
ряды Фурье |
|
|
|
|
||||||||
|
|
|
|
|
уравнений в частных |
|
уравнения |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
производных 2-го |
|
теплопроводности |
|
|||||
|
|
|
|
|
|
|
порядка |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комплексная форма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение задачи Коши |
|
||||
|
|
|
ряда Фурье |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
для волнового |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Уравнение Лапласа |
|
|
|
|
уравнения и уравнения |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
теплопроводности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Обобщенные функции |
|
||
|
|
|
|
|
|
|
Функции Бесселя |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
