4.3.Текущий контроль

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Северо-Западный государственный заочный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика ч.1 (УМК 7,8).pdf

Скачиваний:

Добавлен:

16.02.2016

Размер:

2.14 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

158.a z2 x2 i z2 y2 3 j 2z x y k ,

159.a z sin xi y2 j cos xk ,

160.a 3zi 2 yz 1 j 3x y2 z2 k.

u x,t 1 x at x at

						Тренировочные тесты
							Тест №1
1.	Выберите					интеграл,	к			которому		сводится	интеграл
0	4 x2			4 x2 y2
dx			dy			x2 y2 dz ,		при			переходе	к цилиндрическим
2	0				0
координатам.					4						4
			0	2	4					2	4
	а)	d d 2dz ;					б)	d d 2dz ;
	2			0	0			2		0	0
				2	4					2	4
	в)	d d 2dz ;					г)	d d dz .
			2	0	0				2	0	0
			2						2

2. Объем тела определяется по формуле
а)	1 zx 2 zy 2 dxdy;	б) dxdy; в)	dxdydz; г)
D		D	V

P x, y dx Q x, y dy.

3.	Масса тела определяется по формуле
а) (x, y, z)dxdydz;		б) f (x, y, z)dl;				в) f x, y dxdy;	г)	1 zx 2 zy 2 dxdy.
	V		L			D	D
			2	1	3 y
4.	Вычислите интеграл		dx dy 3 x dz .
			0	0	0	в) 9 / 2;
	а) -10;				б) 10;	в) 9 / 2;		г) 9 / 2.
5.	Если (5xy 3zx)dxdydz				равен 3, то 3(5xy 3zx)dxdydz равен
	T					T
	a) 6;				б) -3;	в) 9;	г) 0.
						161

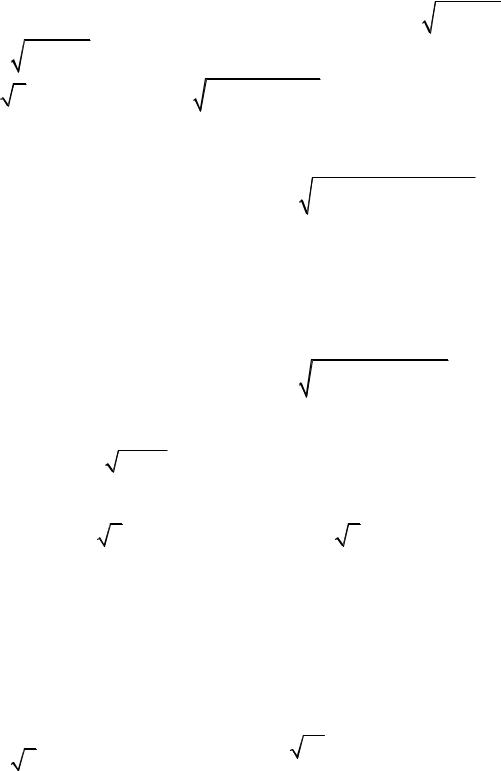
6.	Найдите дифференциал d площади поверхности z 2		x2 y2 .
	а) 2 x2 y2 dxdy ;	б) 4xydxdy ;
	в) 2dxdy ;	г) 1 4x2 4 y2 dxdy .
7.	Формула для вычисления F(x, y, z)d , где : z f (x, y) , имеет вид

а) F(x, y, z)d F(x, y, f (x, y)) 1 ( f 'x )2 ( f 'y )2 dxdy

б) F(x, y, z)d F(x, y, f (x, y))dxdy

в) F(x, y, z)d F(x, y, z)dxdydz

г) F(x, y, z)d F(x, y, f (x, y))

( f 'x )2 ( f 'y )2 dxdy

Вычислите

, где - часть

параболического цилиндра

1 4z

z y2 , задаваемая неравенствами 0 x 2, y x,

z 0 .

а) 2;

б)

2 ;

в) 1;

г)

5 .

Площадь поверхности определяется по формуле

а) f x, y dl;

б) d ;

в) f (x, y, z)dxdydz;

г) (x, y)dxdy.

10.

Найдите

массу

части

поверхности

z x2

y2 , задаваемую

неравенством

z 2 ,

если плотность x, y, z

(при вычислении

двойного интеграла перейдите к полярным координатам).

а) 2 2 ;	б)	3	;	в)	17	;	г) .
а) 2 2 ;	б)		;	в)	2	;	г) .
	2				2
11. Формула для вычисления F(x, y, z)dxdy							, где : z f (x, y) , имеет
вид
вид
а) F(x, y, z)dxdy F(x, y, f (x, y))dxdy
				D
				162

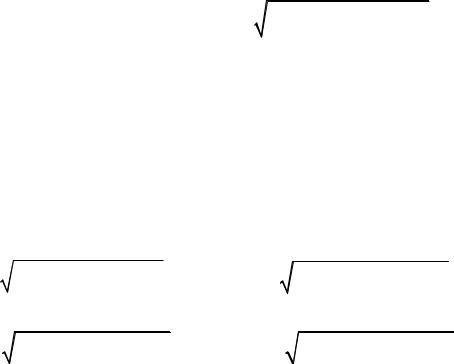
б) F(x, y, z)dxdy F(x, y, f (x, y))		1 ( f 'x )2 ( f 'y )2 dxdy
	D
в) F(x, y, z)dxdy F(x, y, z)dxdydz
	D
г) F(x, y, z)dxdy F(x, y, z)dxdy
	D

12. Направляющий косинус угла между вектором нормали к поверхности

: z f (x, y)

и осью Ох вычисляется по формуле

а)

cos

f 'x

б) cos

( f 'z )2 ( f 'y )2

1 ( f 'x )2 ( f 'y )2

в)

cos

f 'y

г) cos

f 'z

1 ( f 'x )2 ( f 'y )2

13.

Вычислите

2x 8z2 dydz ,

где

внешняя

сторона части

поверхности кругового

цилиндра

ограниченная

плоскостями

z 0 и z 3.

б) 3 ;

в) 27 ;

а) 24;

г) 0.

14.

Вычислите,

используя

формулу

Остроградского-Гаусса,

2x z dydz x 4 y dxdz

3x 2 y dxdy , где

- внешняя

сторона поверхности треугольной пирамиды, образованной координатными плоскостями и плоскостью 2x y 6z 6.

а) 6;	б) 18;		в) 12;	г) 0.
15. Вычислите, используя формулу Стокса			zdx 2 yzdy y2dz , где L -
			L
линия пересечения части		поверхности	эллиптического параболоида
x2 9 y2 9 z ,	лежащей	в первом	октанте,	с координатными

плоскостями. Направление обхода контура идет от оси Ox к оси Oy и к оси

Oz .

а) 18;	б) 27;	в) -18;	г) -27.
		Тест №2

1. Найдите производную скалярного поля U (x, y, z) ln 4 z2 xyz 2
в точке M0 1;1;2	по направлению вектора a 3i 6 j 6k .
а) 3;	б) 1;	в) 0;	г) 4.
	163

2. Найдите градиент скалярного поля U (x, y, z) x2 xcos( y z) в точке

2; 0;

j 2k

j k ;

а) 4i

;

б) 4i

в) 4i

j 2k

;

г) 4i

j k .

Определите,

будет

ли скалярное поле

U (x, y, z) xln

x2 y

гармоническим или нет.

а) гармоническое;

б) негармоническое.

4. Определите уравнения векторных линий поля a

а) x2 y2 C

б) x2 y2 C

в) y xC

г) x y C

5. Определите признак потенциальности векторного поля a :

а) rota

б) rota 0;

в) rota .

6. Определите признак соленоидальности векторного поля a

а) diva

б) diva 0;

в) diva .

Найдите дивергенцию векторного поля a z2i 2 yj

2xyk .

а) 2z ;

б) 2;

в) z2 2 2xy ;

г) -1.

8. Найдите с помощью теоремы Остроградского-Гаусса поток векторного
поля a 2xi xzj 4zk			через внешнюю сторону полной поверхности
тетраэдра,	ограниченного		координатными плоскостями и				плоскостью
2x y 6z 6.
а)	6;	б) 18;	в) 0;		г) 9.		j y2k по
9. Вычислите циркуляцию векторного поля a yzi 4zx2
линии ABFA пересечения с				координатными		плоскостями части
поверхности :		x2 y2 (z 2)2 ,		лежащей в первом октанте.			A, B, F, A -
точки пересечения поверхности с осями Ox,Oy,Oz соответственно.
а) 16;		б) -16;		в) -8;	г) 8 / 3 .
10. Найдите ротор векторного поля a 3y2i 6xyj 2 yzk .
а) 2zi ;		б) 6 yj ;			в) 6 yk ;	г) 8i .
11. Найдите потенциал векторного поля a 2 yzi 2						xz y j 2xyk .
а) 2xy2 z C ;			б) 4xyz y2 C ;
в) 6xyz y2 C ;			г) 2xyz y2 C .
12. Определите вид векторного поля a exi 2 yzj y2k .
			164

а) потенциальное, несоленоидальное;					б) соленоидальное, потенциальное;
в) непотенциальное, несоленоидальное;					г) гармоническое.
13. Найдите U , если U 2x2 y 4 y2					5z 2 .
	а) 4 y 4x ;	б) 3;		в) 4 y 8;		г) 0.
14. Найдите a если a				xyi .
а) xj yk ;		б) O ;		в) j ;	г) выражение не имеет смысла.
15. Выберите выражение, которое для любого векторного поля a							равно числу
ноль					в)
а) a ;		б)	a ;			a ;	г) a.

Тест №3

1.Выберите из приведенных выражений разложение в тригонометрический ряд Фурье функции f x , определенной на промежутке ; и нечетной

на этом промежутке:

а) f x a0 an cos n x bn sin n x ; 2 n 1

	г) f x a0
в) f x bn sin nx;	г) f x a0
n 1	2

б) f x bn sin n x ;

n 1

an cos n x .

n 1

2.Выберите из приведенных выражений разложение в тригонометрический ряд Фурье функции f x , определенной на промежутке ;

а) f x	a0					f x a0
а) f x	a0	an cos n x bn sin n x ;			б)	f x a0	an cos nx;
	2	n 1				2	n 1
	f x a0			bn sin nx ;
в)	f x a0		an cos nx	bn sin nx ;	г)	f x bn cos nx.
		2	n 1			n 1

3.Выберите из приведенных выражений разложение в тригонометрический ряд Фурье функции f x , определенной на промежутке 2;2 и четной на этом

промежутке:

а) f x a0						f x a0			n x
	an cos 2nx			bn sin 2nx ; б)			an cos		n x	;
	an cos 2nx			bn sin 2nx ; б)			an cos			;
2	n 1		n x		г) f x a0	2	n 1	2

в) f x bn sin				;		an cos 2nx .
в) f x bn sin				;		an cos 2nx .
	n 1	2			2	n 1
4. Разложение в ряд Фурье				2π-периодической функции f (x) ,				заданной на
интервале [-π,π) равенствами:
f	0,	при - x 0,				имеет вид
f	(x)			при	0 x .	имеет вид
	2x,			при	0 x .
				165

4(1 ( 1)

)

1 ( 1)

а) f (x) 2

cos nx

sin nx ;

n 1

б) f (x) 4

sin 2nx ;

n 1 2n

1 ( 1)

в) f (x) 2

sin nx .

n 1

4(1 ( 1)n )

( 1)n

г) f (x) 2

cos nx

sin nx

n 1

5. Найти разложение в ряд Фурье по синусам для функции f (x) , заданной на

промежутке

0 x формулой f (x) 1 .

а) искомое разложение будет иметь вид

( 1)n 1

f (x)

sin nx ;

n 1

б) искомое разложение будет иметь вид

f (x) sin x

sin 3x

sin 5x ...

sin(2n 1)x ... ;

2n 1

в) искомое разложение будет иметь вид

f (x)

sin nx .

n 1

6. Найти разложение в ряд Фурье по косинусам для функции f (x) , заданной на

промежутке	0 x формулой f (x)						1	x .
промежутке	0 x формулой f (x)						2	x .
							2
	а) искомое разложение будет иметь вид
f (x)		2	1	cos nx		;
	4

		n 1n2
	б) искомое разложение будет иметь вид
f (x)		1	( 1)n 1		cos nx ;
f (x)	4			n2	cos nx ;
	4	n 1		n2
	в) искомое разложение будет иметь вид
f (x)		2	1 ( 1)n			cos nx .
f (x)						cos nx .
	2	n 1 n2

166

7. Указать,

каким рядом Фурье будет представлена функция, имеющая такой

график

n x

bn sin

;

n 1

aо

б)

cosnx b

sinnx

n 1 n

n x

в)

an cos

bn sin

;

-2

n 1

aо

n x

г)

cos

;

n 1 n

Тест №4

1. Укажите какой из физических процессов определяется уравнением

2u a2 2u :t2 x2

а) процесс распространения тепла; б) процесс диффузии;

в) процесс колебаний струны или колебаний электромагнитного поля; г) стационарный физический процесс, т.е. процесс который не зависит

от времени.


2.	Укажите название уравнения	u	a	2	2u		:
2.	Укажите название уравнения	t	a		x2		:
		t			x2
	а) волновое уравнение;		б) уравнение теплопроводности;
	в) уравнение Лапласа;		г) уравнение Пуассона.
3.	Определите тип уравнения u		2u			2u		2u	0 :
3.	Определите тип уравнения u		x2			y2		z2	0 :
			x2			y2		z2
	а) эллиптического типа;		б) гиперболического типа;
	в) параболического типа;		г) тип уравнения в области меняется.

4. Уравнение U		a2 2U относится к
	t	x2
а)	параболическому типу;		б)	гиперболическому типу;
в)	смешанному типу;		г)	эллиптическому типу.

5.Определите, решением какой задачи является формула

An cos n lat Bn sin n lat sin nl x :

n 1

а) решением задачи Коши для волнового уравнения методом

167

Даламбера; б) решением уравнения теплопроводности при заданных начальных и

граничных условиях методом Фурье; в) решением волнового уравнения при заданных начальных и

граничных условиях методом Фурье; г) решением задачи Коши для уравнения теплопроводности, т.е.

интеграла Пуассона.

6. Определите, решением какой задачи является формула

а) решением задачи Коши для волнового уравнения методом Даламбера;

б) решением уравнения теплопроводности при заданных начальных и граничных условиях методом Фурье;

в) решением волнового уравнения при заданных начальных и граничных условиях методом Фурье;

г) решением задачи Коши для уравнения теплопроводности, т.е. интеграла Пуассона.

		an 2
				t

7. Формула U (x,t)	Cne		l	sin	n x	дает решение
					l
	n 1

a)уравнения распространения тепла в конечном стержне;

b)уравнения колебания конечной струны;

c)уравнения колебания бесконечной струны;

d)уравнения Лапласа.

8.Определите формулу для решения методом Фурье волнового уравнения :

а) u x,t X x T t ;

б) u x,t

X x

;

в) u x,t X x T

t .

T t

Ответы на тренировочные тесты

№

№ вопроса

теста

168

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1413 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.02.2016164.35 Кб8Маркетингт.doc
#
16.02.2016120.32 Кб16Мат.ч.1.doc
#
16.02.201646.08 Кб18Мат.ч.2.doc
#
16.02.2016772.83 Кб54Математика для 1 курса.pdf
#
18.11.20185.16 Mб34МАТЕМАТИКА методичка.doc
#
16.02.20162.14 Mб70Математика ч.1 (УМК 7,8).pdf
#
16.02.20161.56 Mб43Математика ч.2 (УМК).pdf
#
16.02.20162.03 Mб38Математика часть 1 УМК.pdf
#
16.02.201644.99 Кб25Математика(шифр 03).docx
#
16.02.20162.68 Mб45МатериаловедениеМУРЛ2007.doc
#
16.02.20165.56 Mб90МатериаловедениеУМК2008.doc