
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:Начерталка / 13-14г. ПОВЕРХНОСТЬ..ppt
X
- •Поверхности
- •Поверхности
- •КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
- •ЗНАЧИТЕЛЬНЫЙ КЛАСС ПОВЕРХНОСТЕЙ ФОРМИРУЕТСЯ ДВИЖЕНИЕМ ОКРУЖНОСТИ ПОСТОЯННОГО ИЛИ ПЕРЕМЕННОГО РАДИУСА. ЭТО ТАК НАЗЫВАЕМЫЕ
- •ЕСЛИ ЖЕ ГРУППИРОВАТЬ ПОВЕРХНОСТИ ПО ЗАКОНУ ДВИЖЕНИЯ ОБРАЗУЮЩЕЙ ЛИНИИ И ПРОИЗВОДЯЩЕЙ ПОВЕРХНОСТИ, ТО
- •Образование поверхности вращения
- •ТАК СОЗДАЕТСЯ КАРКАС ПОВЕРХНОСТИ, СОСТОЯЩЕЙ ИЗ МНОЖЕСТВА ОКРУЖНОСТЕЙ , ПЛОСКОСТИ КОТОРЫХ РАСПОЛОЖЕНЫ ПЕРПЕНДИКУЛЯРНО
- •СФЕРА – ОБРАЗУЕТСЯ ВРАЩЕНИЕМ ОКРУЖНОСТИ ВОКРУГ ЕЁ ДИАМЕТРА . ПРИ СЖАТИИ ИЛИ РАСТЯЖЕНИИ
- •ТОР – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ОКРУЖНОСТИ ВОКРУГ ОСИ, НЕ ПРОХОДЯЩЕЙ ЧЕРЕЗ ЦЕНТР ОКРУЖНОСТИ
- •ПАРАБОЛОИД ВРАЩЕНИЯ – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ПАРАБОЛЫ ВОКРУГ СВОЕЙ ОСИ
- •ГИПЕРБОЛОИД ВРАЩЕНИЯ – РАЗЛИЧАЮТ ОДНО И ДВУХ ПОЛОСТНОЙ ГИПЕРБОЛОИДЫ ВРАЩЕНИЯ. ПЕРВЫЙ ПОЛУЧАЕТСЯ ПРИ
- •Винтовые поверхности образуются винтовым движением некоторой линии – образующей.
- •АЛГОРИТМИЧЕСКАЯ ЧАСТЬ:
- •ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА (ПОВЕРХНОСТИ КАТАЛАНА)
- •В ЗАВИСИМОСТИ ОТ ФОРМЫ НАПРАВЛЯЮЩИХ ОБРАЗУЮТСЯ ТРИ ЧАСТНЫХ ВИДА ПОВЕРХНОСТЕЙ. ЦИЛИНДРОИД. ЦИЛИНДРОИДОМ НАЗЫВАЕТСЯ
- •КОНОИД. КОНОИДОМ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ ПО ДВУМ НАПРАВЛЯЮЩИМ, ОДНА ИЗ
- •ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД. ГИПЕРБОЛИЧЕСКИМ ПАРАБОЛОИДОМ ИЛИ КОСОЙ ПЛОСКОСТЬЮ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ,
- •Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой
- •Цилиндрическая поверхность
- •Коническая поверхность
- •Однополостный гиперболоид
- •Вогнутый тор (глобоид)
- •Сфера
- •Выпуклый тор
- •Эллипсоид
- •Открытый тор (окружность m вращается вокруг оси i )
- •Закрытый тор
- •Закрытый кольцевой тор (самопересекающийся)
- •Гранные
- •Гранные поверхности
- •Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей
- •Пирамидальная поверхность
- •Призматическая поверхность
- •ПРАВИЛЬНЫЙ ШЕСТИГРАННИК (КУБ) ИЛИ ГЕКСАЭДР - ЧАСТНЫЙ СЛУЧАЙ ПРЯМОЙ ПРИЗМЫ, У КОТОРОЙ ОСНОВАНИЯ
- •ПРАВИЛЬНЫЙ ВОСЬМИГРАННИК ИЛИ ОКТАЭДР - МНОГОГРАННИК, СОСТОЯЩИЙ ИЗ ВОСЬМИ ГРАНЕЙ - ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ,
- •ПРАВИЛЬНЫЙ ДВАДЦАТИГРАННИК ИЛИ ИКОСАЭДР СОСТОИТ ИЗ ДВАДЦАТИ ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ, СОЕДИНЕННЫХ ПО ПЯТИ В
- •Задача
- •Поверхности
- •Линии, образующие внешний
- •Линейчатые поверхности вращения
- •Определитель
- •Определитель поверхности сферы
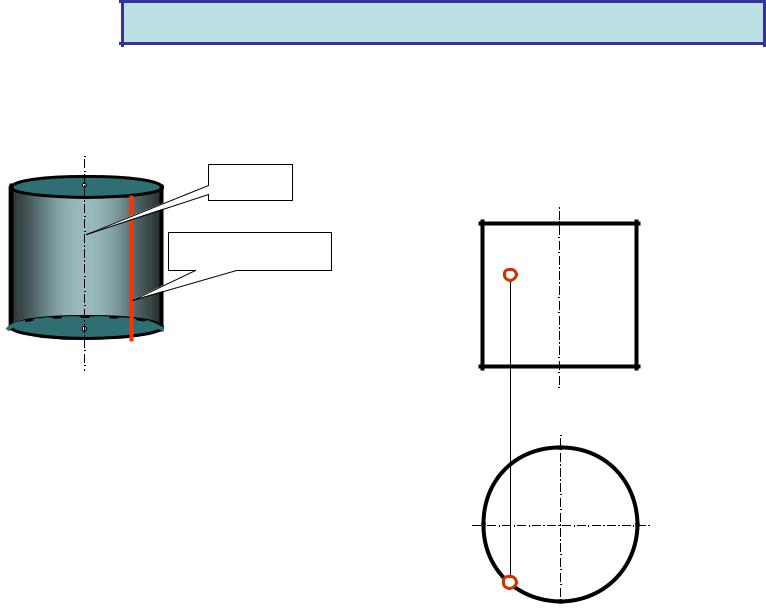
- •цилиндр
- •цилиндр
- •Точка принадлежит поверхности, если она принадлежит линии, расположенной на этой поверхности
- •Линейчатые поверхности вращения
- •Линейчатые поверхности вращения
- •Линейчатые поверхности вращения
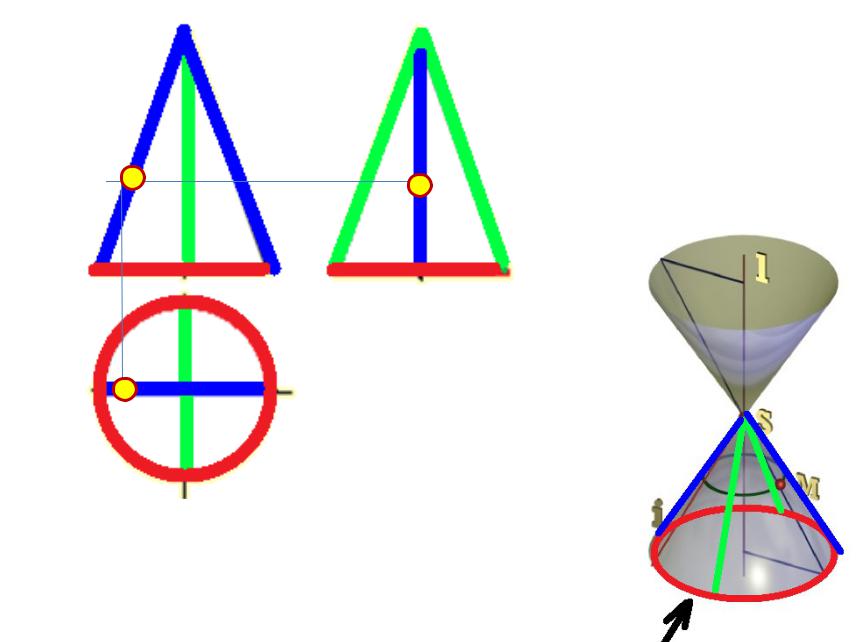
- •Точка на поверхности конуса
- •Комплексный чертеж
- •Главный меридиан,
- •Главный
- •Главный
- •Экватор
- •Точка на поверхности сферы
- •Точка на поверхности сферы
- •Экватор
- •Главный меридиан, параллельный П3
- •Радиус
- •Обычно геометрические тела изображаются в их простейших положениях, наиболее выгодных
- •***Построение комплексных чертежей
- •Среди точек кривой выделяют опорные точки:

Линии, образующие внешний
контур |
геометрического тела, |
называют |
О Ч Е Р К О М . |
Различают горизонтальный,
фронтальный и профильный очерки.
ОЧЕРКИ проекций всегда видим. Видимость линий, расположенных внутри очерка определяется при помощи конкурирующих точек.
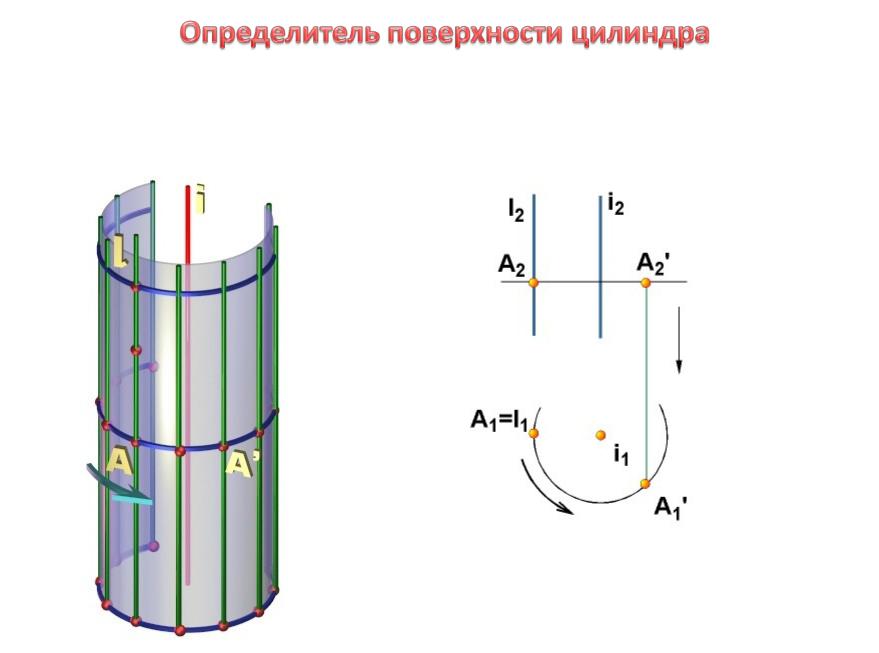
Линейчатые поверхности вращения
Цилиндрическая поверхность –поверхность, образованная вращением прямолинейной образующей вокруг оси.
Г ( l, i)[ l ||i ]– цилиндрическая поверхность
ось |
|
Образующая |
12 |
11
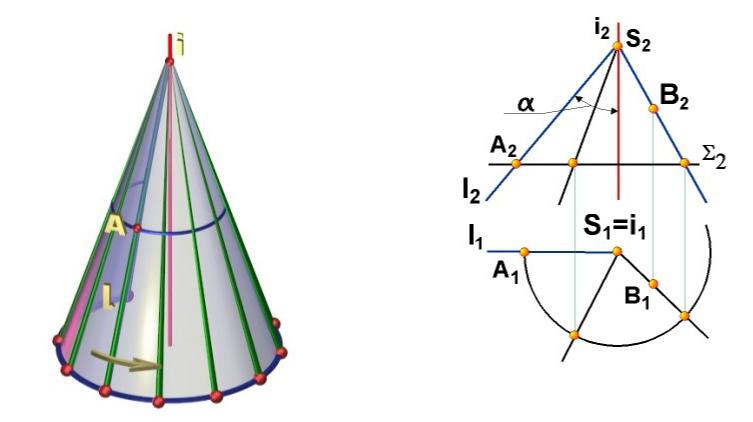
Определитель
проверхности конуса
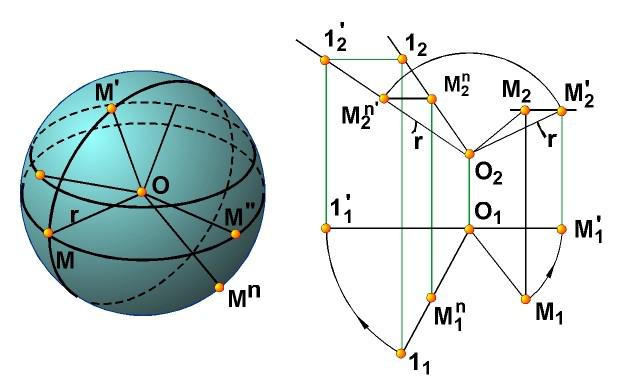
Определитель поверхности сферы
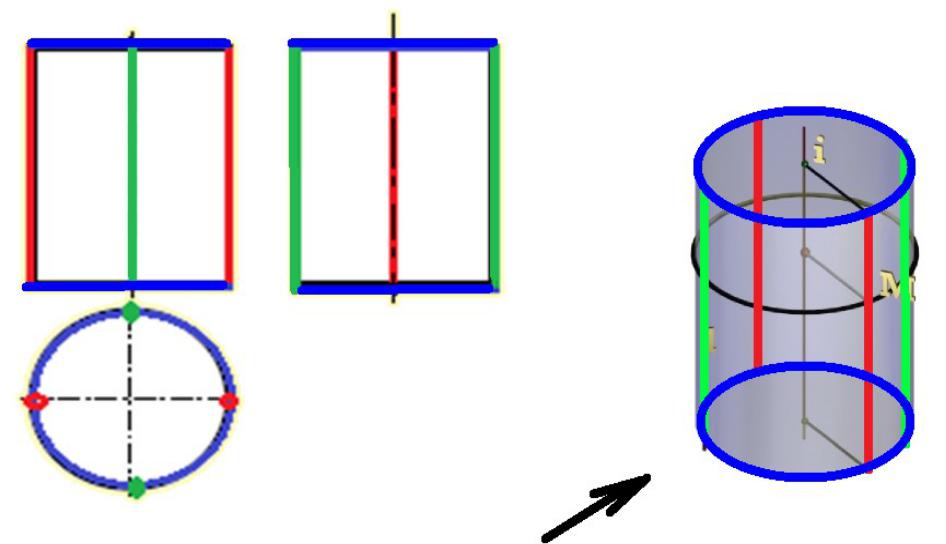
цилиндр
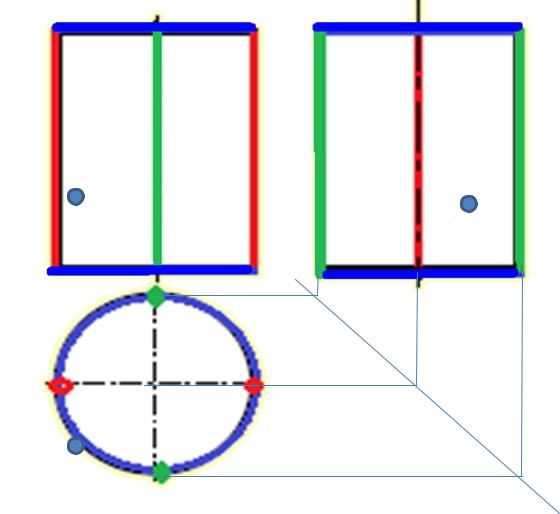
цилиндр
12 |
13 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11
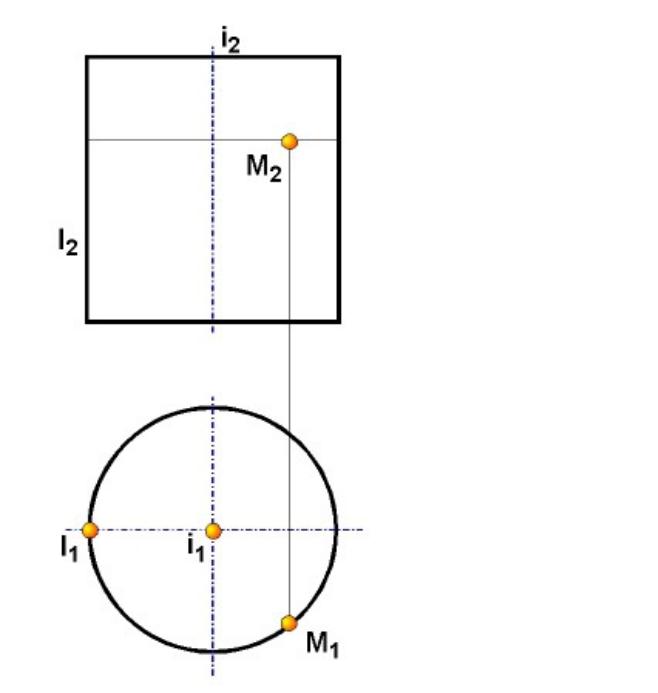
Точка принадлежит поверхности, если она принадлежит линии, расположенной на этой поверхности
Линия принадлежит поверхности, если каждая ее точка принадлежит этой поверхности
Соседние файлы в папке Начерталка
