- •Поверхности
- •Поверхности
- •КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
- •ЗНАЧИТЕЛЬНЫЙ КЛАСС ПОВЕРХНОСТЕЙ ФОРМИРУЕТСЯ ДВИЖЕНИЕМ ОКРУЖНОСТИ ПОСТОЯННОГО ИЛИ ПЕРЕМЕННОГО РАДИУСА. ЭТО ТАК НАЗЫВАЕМЫЕ
- •ЕСЛИ ЖЕ ГРУППИРОВАТЬ ПОВЕРХНОСТИ ПО ЗАКОНУ ДВИЖЕНИЯ ОБРАЗУЮЩЕЙ ЛИНИИ И ПРОИЗВОДЯЩЕЙ ПОВЕРХНОСТИ, ТО
- •Образование поверхности вращения
- •ТАК СОЗДАЕТСЯ КАРКАС ПОВЕРХНОСТИ, СОСТОЯЩЕЙ ИЗ МНОЖЕСТВА ОКРУЖНОСТЕЙ , ПЛОСКОСТИ КОТОРЫХ РАСПОЛОЖЕНЫ ПЕРПЕНДИКУЛЯРНО
- •СФЕРА – ОБРАЗУЕТСЯ ВРАЩЕНИЕМ ОКРУЖНОСТИ ВОКРУГ ЕЁ ДИАМЕТРА . ПРИ СЖАТИИ ИЛИ РАСТЯЖЕНИИ
- •ТОР – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ОКРУЖНОСТИ ВОКРУГ ОСИ, НЕ ПРОХОДЯЩЕЙ ЧЕРЕЗ ЦЕНТР ОКРУЖНОСТИ
- •ПАРАБОЛОИД ВРАЩЕНИЯ – ОБРАЗУЕТСЯ ПРИ ВРАЩЕНИИ ПАРАБОЛЫ ВОКРУГ СВОЕЙ ОСИ
- •ГИПЕРБОЛОИД ВРАЩЕНИЯ – РАЗЛИЧАЮТ ОДНО И ДВУХ ПОЛОСТНОЙ ГИПЕРБОЛОИДЫ ВРАЩЕНИЯ. ПЕРВЫЙ ПОЛУЧАЕТСЯ ПРИ
- •Винтовые поверхности образуются винтовым движением некоторой линии – образующей.
- •АЛГОРИТМИЧЕСКАЯ ЧАСТЬ:
- •ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА (ПОВЕРХНОСТИ КАТАЛАНА)
- •В ЗАВИСИМОСТИ ОТ ФОРМЫ НАПРАВЛЯЮЩИХ ОБРАЗУЮТСЯ ТРИ ЧАСТНЫХ ВИДА ПОВЕРХНОСТЕЙ. ЦИЛИНДРОИД. ЦИЛИНДРОИДОМ НАЗЫВАЕТСЯ
- •КОНОИД. КОНОИДОМ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ ПО ДВУМ НАПРАВЛЯЮЩИМ, ОДНА ИЗ
- •ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОИД. ГИПЕРБОЛИЧЕСКИМ ПАРАБОЛОИДОМ ИЛИ КОСОЙ ПЛОСКОСТЬЮ НАЗЫВАЕТСЯ ПОВЕРХНОСТЬ, ОБРАЗОВАННАЯ ДВИЖЕНИЕМ ПРЯМОЛИНЕЙНОЙ ОБРАЗУЮЩЕЙ,
- •Поверхностью параллельного переноса называется поверхность, образованная поступательным плоскопараллельным перемещением образующей - плоской кривой
- •Цилиндрическая поверхность
- •Коническая поверхность
- •Однополостный гиперболоид
- •Вогнутый тор (глобоид)
- •Сфера
- •Выпуклый тор
- •Эллипсоид
- •Открытый тор (окружность m вращается вокруг оси i )
- •Закрытый тор
- •Закрытый кольцевой тор (самопересекающийся)
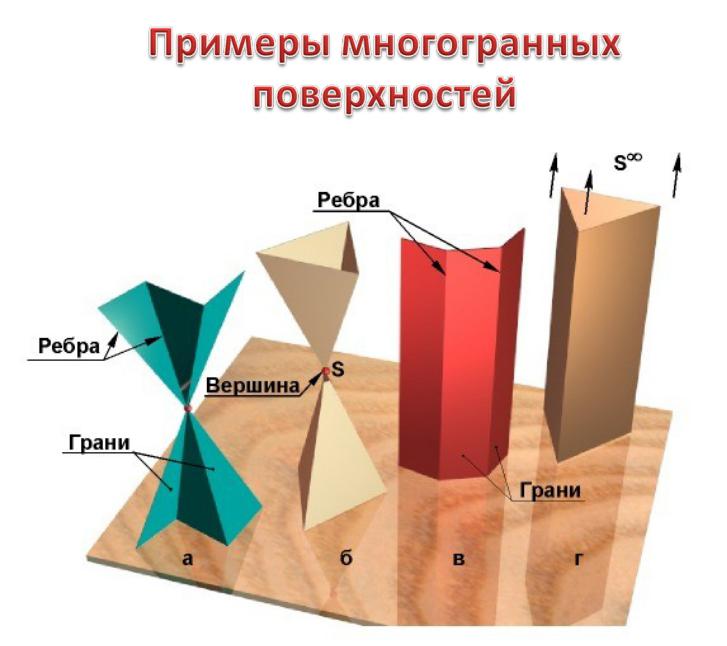
- •Гранные
- •Гранные поверхности
- •Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей
- •Пирамидальная поверхность
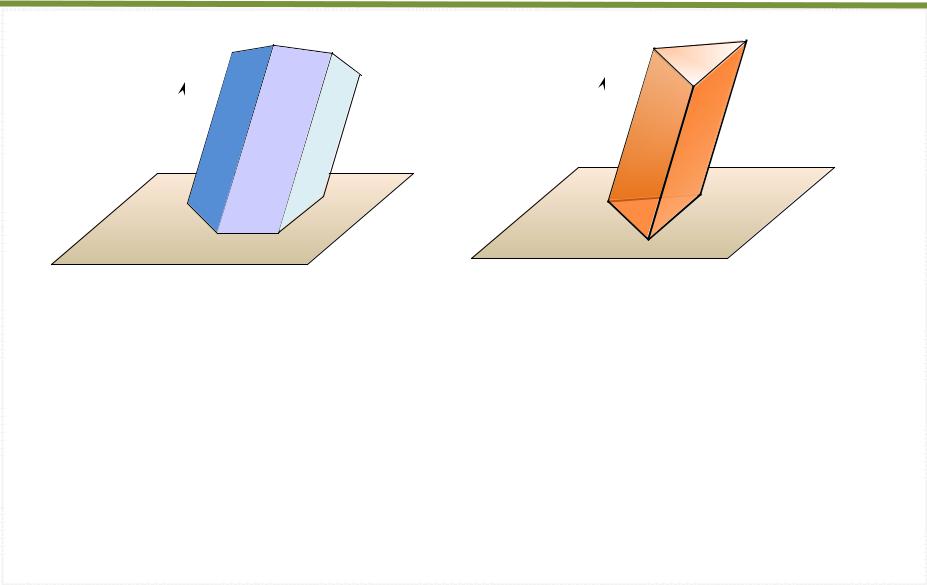
- •Призматическая поверхность
- •ПРАВИЛЬНЫЙ ШЕСТИГРАННИК (КУБ) ИЛИ ГЕКСАЭДР - ЧАСТНЫЙ СЛУЧАЙ ПРЯМОЙ ПРИЗМЫ, У КОТОРОЙ ОСНОВАНИЯ
- •ПРАВИЛЬНЫЙ ВОСЬМИГРАННИК ИЛИ ОКТАЭДР - МНОГОГРАННИК, СОСТОЯЩИЙ ИЗ ВОСЬМИ ГРАНЕЙ - ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ,
- •ПРАВИЛЬНЫЙ ДВАДЦАТИГРАННИК ИЛИ ИКОСАЭДР СОСТОИТ ИЗ ДВАДЦАТИ ПРАВИЛЬНЫХ ТРЕУГОЛЬНИКОВ, СОЕДИНЕННЫХ ПО ПЯТИ В
- •Задача
- •Поверхности
- •Линии, образующие внешний
- •Линейчатые поверхности вращения
- •Определитель
- •Определитель поверхности сферы
- •цилиндр
- •цилиндр
- •Точка принадлежит поверхности, если она принадлежит линии, расположенной на этой поверхности
- •Линейчатые поверхности вращения
- •Линейчатые поверхности вращения
- •Линейчатые поверхности вращения
- •Точка на поверхности конуса
- •Комплексный чертеж
- •Главный меридиан,
- •Главный
- •Главный
- •Экватор
- •Точка на поверхности сферы
- •Точка на поверхности сферы
- •Экватор
- •Главный меридиан, параллельный П3
- •Радиус
- •Обычно геометрические тела изображаются в их простейших положениях, наиболее выгодных
- •***Построение комплексных чертежей
- •Среди точек кривой выделяют опорные точки:
Закрытый тор
А2
 экватор
экватор
А
А1

Закрытый кольцевой тор (самопересекающийся)

Гранные
поверхности
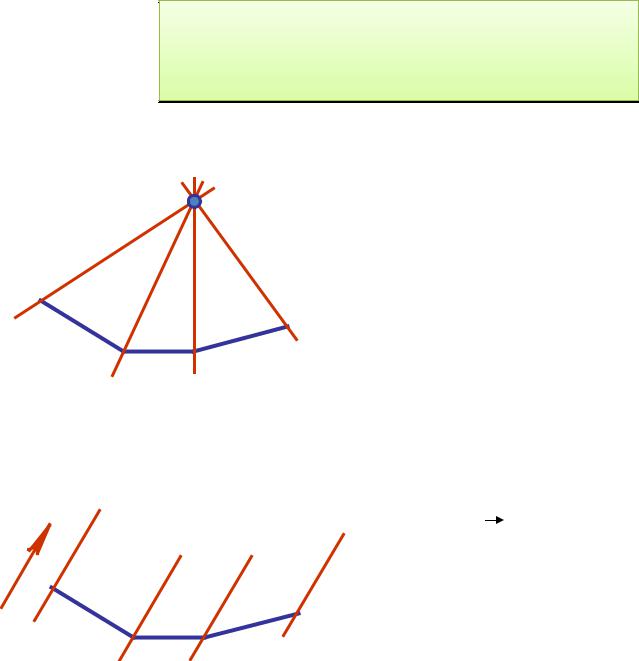
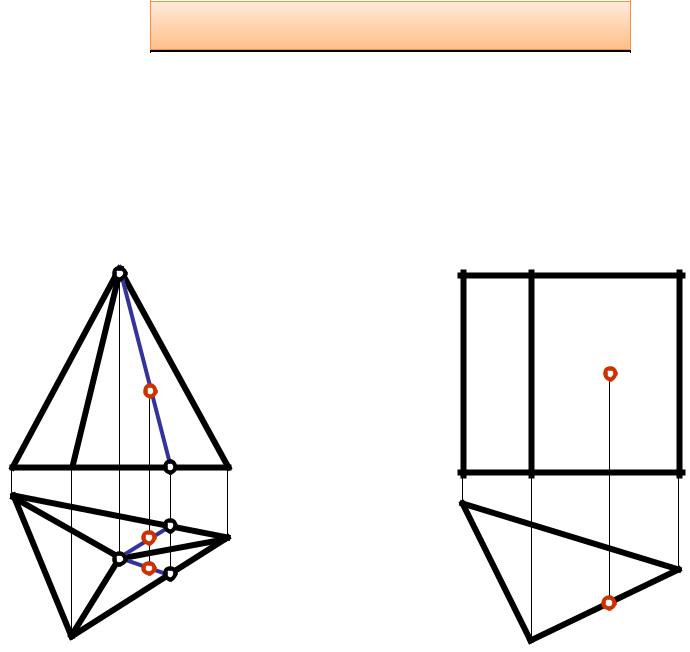
Пирамидальная поверхность – это линейчатая поверхность, образованная перемещением прямой линии, проходящей через фиксированную точку S (вершину), по ломанной направляющей m
S
(l,m)[ S l, l m]
l
m
Призматическая поверхность – это линейчатая поверхность, образованная перемещением прямой линии по ломанной направляющей m
и движущейся параллельно некоторому заданному направлению s
(l,m) [ l || s, l m]
S l
m
Гранные поверхности
Многогранником называют замкнутые пространственные фигуры, ограниченные плоскими многоугольниками.
Грани - многоугольники многогранника. Ребра – линии пересечения граней. Вершины – точки пересечения ребер.
S2
N N 1 |
M2 |
|
2 |
2 |
|
А2 |
В2 |
|
12 |
С2 |
А2 |
В2 |
С2 |
А1 |
|
N11 |
1 |
1 |
А1 |
|
|
|
|
1 |
С1 |
|
|
||
|
S1 |
|
|
|
|
|
|
|
N1 |
|
|
|
|
С1 |
|
|
|
11 |
|
|
|
||
|
|
|
|
|
|
M1 |
|
|
В1 |
|
|
|
|
|
|
|
|
|
|
|
В1 |
|
|
|
|
|
|
|
|
|
Многогранные поверхности – это поверхности, образованные частями (отсеками) пересекающихся плоскостей
Многогранником называется тело, ограниченное многогранной поверхностью,
состоящей из плоских многоугольников
Отсеки плоскостей называются гранями, а линии их пересечения – ребрами
Точки пересечения ребер называются
вершинами

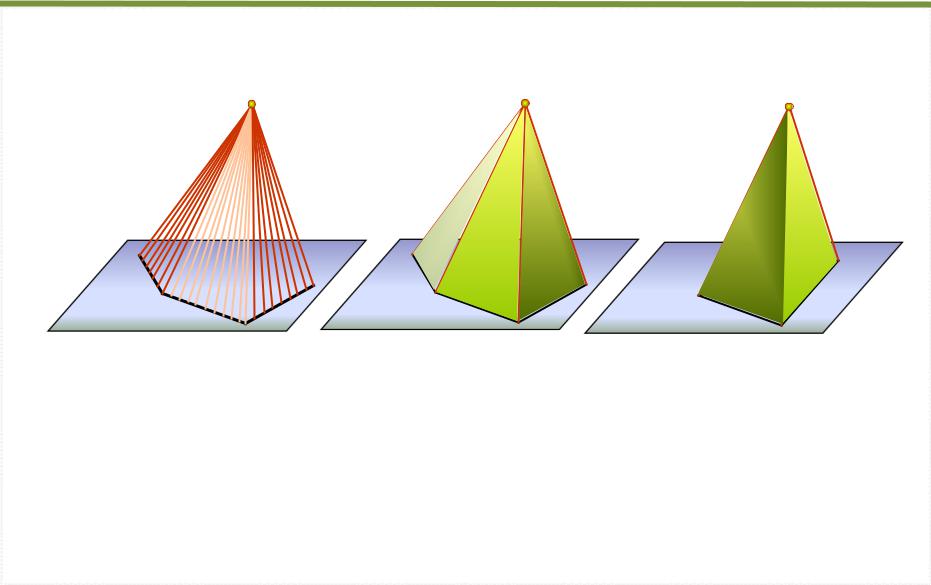
Пирамидальная поверхность |
Пирамида |
|
|
|
m – замкнутый контур |
S |
|
S |
S |
ℓ |
|
|
|
m |
m |
|
m |
Если направляющая m |
Поверхность с замкнутой |
||
ломаная, а все |
|
ломаной направляющей |
|
образующие ℓ |
|
|
(m), общей точкой |
пересекаются в одной |
пересечения образующих |
||
точке, такая поверхность |
|
ребер и граней |
|
называется пирамидальной |
называется пирамидой |
||
Призматическая поверхность |
Призма |
S ℓ
ℓ
m |
Если все образующие |
поверхности параллельны – поверхность
называется
призматической
S ℓ
ℓ
m |
Поверхность с замкнутой ломаной направляющей
(m) (основанием) и
взаимно параллельными ребрами – призма