Решение

На основании закона сохранения энергии потенциальная энергия тела расходуется на работу против сил трения на наклонном и горизонтальном участках

W_n = A_тр, W_n = 0 – m g h,

 m g h = A_тр1 + А_тр2. (1)

Работа силы трения равна А =  F_тр s. По закону трения F_тр =  N, где N – реакция опоры.

На наклонной плоскости N = mg сos . На горизонтальной поверхности N = mg, поэтому A_тр1 =   mg сos  s, A_тр2 =   mg s.

Подставив выражения для работы в формулу (1), получим

 mg h =   mg сos  s -  mg s,

откуда найдём коэффициент трения

Подставив числовые значения, получим

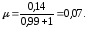
Ответ:  = 0,07.

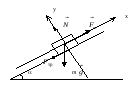
Задача 3. Автомобиль массой 2 тонны движется в гору. Уклон горы равен 4 м на каждые 100 м пути. Коэффициент трения равен 0,08 (рис. 5.5). Найти: а) работу, совершённую двигателем автомобиля на пути в 3 км; б) мощность, развиваемую двигателем, если известно, что этот путь был пройден за 4 мин.

Дано:

= 0

m = 2·10^-3 кг

sin = 0,04

 = 0,08

s = 3000 м

t = 240 с

А - ? N - ?

Рис. 5.5

Решение

На автомобиль, движущийся по наклонной плоскости, действуют mg – сила тяжести, N – сила нормальной реакции наклонной плоскости, F_т – сила тяги двигателя, F_тр – сила трения.

Работа, совершённая двигателем автомобиля, равна

A = F_т s, (1)

мощность

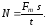
Для нахождения этих величин необходимо найти силу тяги F_т.

По II закону Ньютона Выбирая направление осейX и Y и проецируя на них векторное уравнение II закона Ньютона для тела, получаем

 F_тр – mg sin  + F_т = m а;

N – mg cos  = 0,

тогда N = mg cos ;

F_т = m a + mg sin  + F_тр.

По закону трения

F_тр =  N =  mg cos ;

F_т = ma + mg sin  +  mg cos .

Ускорение, с которым движется автомобиль, найдём из формулы пути равноускоренного движения. Так как = 0, тои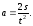

После подстановки в формулу (1) получим

=

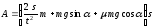Подставив числовые значения, получим

7·10⁶ Дж;

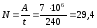кВт.

Ответ: А = 7·10⁶ Дж; N = 29,4 кВт.

Задача 4. Диск массой 1 кг и диаметром 60 см вращается вокруг оси, проходящей через центр перпендикулярно его плоскости, делая 20 . Какую работу надо совершить, чтобы остановить диск?

Дано:

m = 1 кг

R = 0,3 м

= 20

 = 0

А - ?

Решение

Работа, которую совершает внешняя сила, равна изменению кинетической энергии вращающегося диска: A = W_k , W_k = 0 – W_k1

Кинетическая энергия диска, вращающегося вокруг своей оси

где J – момент инерции диска,  - угловая скорость диска.

Для диска  = 2  . Тогда .

Подставив числовые значения, получим

А = 1·0,3²·3,14²·20² = 360 Дж.

Ответ: А = 360 Дж.

Задача 5. Вентилятор вращается со скоростью, соответствующей 900 . После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки 75 оборотов. Работа сил торможения равна 44,4 Дж. Найти: а) момент инерции вентилятора; б) момент силы торможения.

Дано:

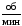= 900 = 15

 = 0

N = 75 об

A = 44,4 Дж

J - ? M - ?