Решение
Платформа приобретает скорость u в результате взаимодействия со снарядом. Сила взаимодействия системы тел платформа – снаряд является внутренней силой и не изменяет импульс системы. Внешними силами являются сила тяжести, сила нормальной реакции рельсов и сила трения. Если пренебречь действием силы трения на платформу во время удара, то, поскольку силы тяжести и нормальной реакции рельсов строго вертикальны, можно считать, что проекция вектора импульса системы на горизонтальное направление остаётся постоянной.
Запишем для снаряда и платформы закон сохранения импульса при неупругом ударе в векторном виде:
(1)
Выбрав направление оси X совпадающим с направлением полёта снаряда, спроецируем уравнение (1) на ось X, вдоль которой происходит движение платформы для каждого из трёх случаев:
1)
,
откуда
2)
-
8
.
3)
.
Ответ:
=
2
;
=8
;
=
12
.
Задача 6. Деревянный шарик падает вертикально вниз с высоты 2 м без начальной скорости. Коэффициент восстановления при ударе шарика о пол считать равным 0,5. Найти: а) высоту, на которую поднимается шарик после удара о пол; б) количество тепла, которое выделиться при этом ударе. Масса шарика 100 г.
Дано:
=
2 м
V0 = 0
k = 0,5
m = 0,1 кг
-
?
Q -?
Решение
Падая
с высоты
,
шарик падает на пол со скоростью V1,
а отскакивает вверх со скоростью V2.
По
определению коэффициент восстановления
k
=
По
закону сохранения энергии
и
По
закону сохранения энергии
и
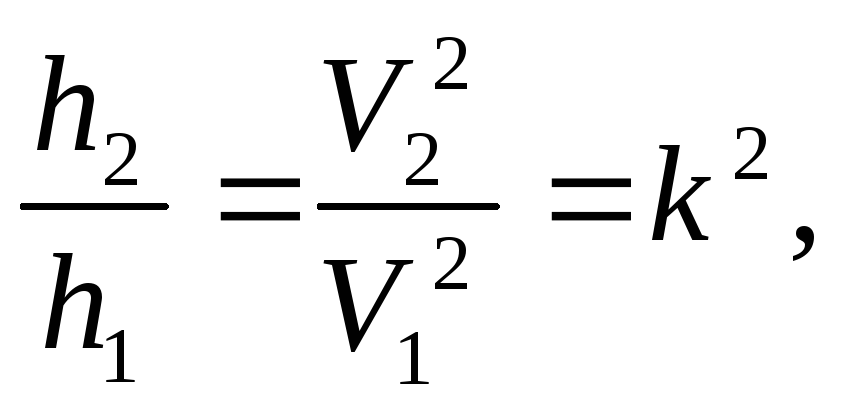откуда
=
.
=
. 2 = 0,5 м.
Количество тепла, выделившегося при ударе шарика о пол, равно разности кинетических энергий тела до удара и после удара:
Дж.
Ответ:
= 0,5 м;
= 1,48 Дж.
Задача
7. На скамье
Жуковского стоит человек и держит в
вытянутых руках гири по 10 кг каждая.
Расстояние между гирями 1,5 м. Скамья
вращается с частотой
=
1
.
Как изменится частота вращения скамьи
и какую работу произведёт человек, если
он сблизит руки так, что расстояние
между гирями уменьшится до 40 см? Суммарный
момент инерции человека и скамьи
относительно оси вращенияJ0
= 2,5 кг.м2.
Ось вращения проходит через центр масс
человека и скамьи (рис.4.6).
Дано:
=
= m
= 10 кг
1
= 1,5 м
2
= 0,4 м
=
1
J0
= 2,5 кг.м2
-
? А
- ?
Рис.4.6
Решение
Частота вращения скамьи Жуковского изменяется в результате действий, производимых человеком при сближении гирь. В системе тел скамья – человек – гири взаимодействия этих тел являются внутренними. Все тела системы совершают только вращательное движение вокруг одной и той же оси; они не изменяют момент импульса системы. Внешние силы – сила тяжести, сила нормальной реакции – параллельны оси вращения. (Сила трения в оси не учитывается). Моменты всех внешних сил относительно вертикальной оси вращения скамьи равны нулю. Следовательно, момент импульса системы тел остаётся постоянным. По закону сохранения момента импульса
,
(1)
где
и
-
моменты импульса системы до и после
сближения гирь.