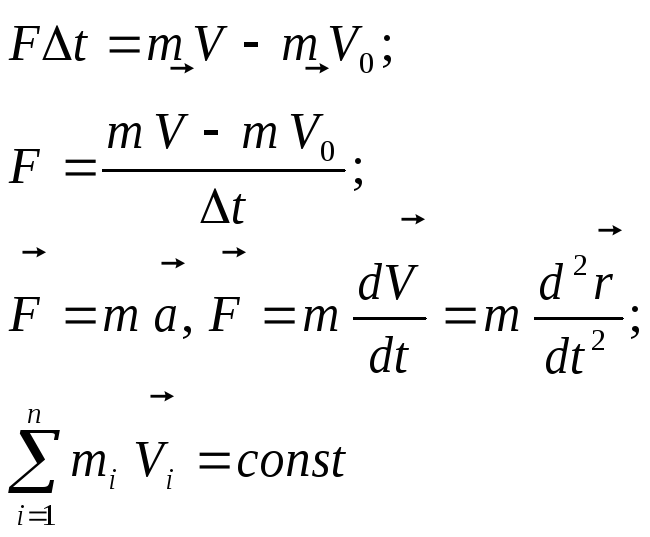Занятие 4

ЗАКОНЫ СОХРАНЕНИЯ ИМПУЛЬСА И МОМЕНТА

ИМПУЛЬСА

Учебная цель: добиться понимания физической сущности законов сохранения импульса и момент импульса. Привить навыки самостоятельного решения задач с применением этих законов.

Литература

Основная: Детлаф А. А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989.– Гл.5, § 5.1 – 5.3.

Дополнительная: Савельев И.В. Курс общей физики. – М.: Наука, 1987. – Т.1, гл.3, § 27 – 29.

Контрольные вопросы для подготовки к занятию

1. Что называется импульсом тела? Импульсом силы? Их единицы измерения.

2. Cформулируйте определение замкнутой системы тел.

3. Сформулируйте и запишите закон сохранения импульса для системы тел?

4. Что называется коэффициентом восстановления? От чего он зависит?

5. Что называется ударом, упругим ударом, неупругим ударом?

6. Что называется моментом импульса? Единица измерения в СИ.

7. Сформулируйте и запишите закон сохранения момента импульса для системы тел и одного тела. Для каких систем он справедлив?

Краткие теоретические сведения и основные формулы

Импульсом тела называется физическая векторная величина, равная произведению массы тела на его скорость и имеющая направление скорости

Импульс – это мера механического движения тела с заданной массой.

Для изменения импульса тела необходимо, чтобы на него подействовала сила. Изменение импульса будет зависеть не только от величины силы, но также и от времени её действия.

Импульсом силы называется векторная физическая величина равная произведению силы и времени её действия, т.е. [H^.c].

Понятием импульса силы широко пользуются при решении задач о движении нескольких взаимодействующих тел.

Мысленно выделенная совокупность материальных точек (тел), движущихся согласно законам классической механики и взаимодействующих друг с другом и с телами, не включёнными в состав этой совокупности, называется механической системой. Силы взаимодействия между телами механической системы называются внутренними. Силы, с которыми взаимодействуют тела, не входящие в систему, называются внешними.

Механическая система тел, на которую не действуют внешние силы называется замкнутой, или изолированной. В изолированной системе геометрическая сумма импульсов входящих в неё тел, остаётся постоянной, то есть

Закон сохранения импульса нашёл широкое применение при ударе тел.

Ударом называется кратковременное взаимодействие тел, возникающее в результате их столкновения.

При соударении тел друг с другом они претерпевают деформацию. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и в так называемую внутреннюю энергию тел.

Для учёта потерь энергии вводится коэффициент восстановления, который зависит только от физических свойств материала тел. Он определяется отношением нормальной составляющей (по отношению к поверхности соударения) относительной скорости после удара к её величине до удара(рис.4.1):

Удар называется абсолютно упругим, если после удара возникшие в телах деформации полностью исчезают (кинетическая энергия тела до и после удара остаётся неизменной, k = 1).

Удар называется абсолютно неупругим, если после удара возникшие в телах деформации полностью сохраняются (k = 0). После абсолютно неупругого удара тела движутся с общей скоростью.

Рис.4.1

При неупругом центральном ударе двух тел с массами и общая скорость движение этих тел после удара может быть определена из закона сохранения импульса:

где - скорость первого тела до удара; - скорость второго тела до удара.

Часть кинетической энергии тел до удара пойдёт на работу деформации

При упругом центральном ударе тела после удара будут двигаться с различными скоростями. Скорость первого тела после удара

Скорость второго тела после удара

При решении задач механики в незамкнутых системах применить закон сохранения импульса можно, если:

а) внешние силы действуют, но результирующая этих сил равна нулю;

б) проекция суммы всех внешних сил на какое-то направление равна нулю, следовательно, проекция импульса на это направление сохраняется, хотя сам вектор импульса не остаётся постоянным.

Моментом импульса тела относительно неподвижной оси называется векторная физическая величина, равная произведению момента инерции тела относительно той же оси на угловую скорость тела:

Момент импульса системы тел есть векторная сумма моментов импульсов всех тел системы

Закон сохранения момента импульса: есть результирующий момент внешних сил, приложенных к системе, равен нулю , то момент импульса системы есть величина постоянная, то есть

Для двух тел:

где J₁, J₂, , – момент инерции и угловые скорости тел до взаимодействия; - те же величины после взаимодействия.

Для одного тела, момент инерции которого может меняться:

где J₁ и J₂ – начальное и конечное значение момента инерции; и – начальная конечная угловые скорости тела.

В задачах по общему курсу физики обычно рассматривают вращение твердого тела лишь вокруг неподвижной оси или оси, перемещающейся в пространстве параллельно самой себе. В этом случае физические величины, характеризующие вращательное движение тела направлены вдоль оси вращения. Это позволяет упростить запись уравнений вращательного движения тела. Выбрав ось вращения за ось проекций, все уравнения можно записать в скалярной форме. При этом знаки величин, , М, L определяют следующим образом. Некоторое направление вращения (по часовой стрелке или против неё) выбирают за положительное. Величины , L, М берутся со знаком плюс, если их направление соответствует выбранному положительному направлению, в противном случае – со знаком минус. Знак величины  всегда совпадает со знаком М.

При ускоренном вращении тела знаки всех четырёх величин совпадают; при замедленном движении две пары величин - , L и М,  - имеют противоположные знаки.

Сопоставление основных величин и уравнений, определяющих вращательное движение тела вокруг неподвижной оси и его поступательное движение, подчёркивающее их аналогию, приведено в таб. 4.1.

Т а б л и ц а 4.1

Поступательное движение	Вращательное движение
Равнодействующая внешних сил Основное уравнение динамики	Суммарный момент внешних сил – М Основное уравнение динамики: