Логарифмічне диференціювання

При обчисленні похідної від логарифма добутку, частки, степеня або кореня, для спрощення знаходження похідної роблять попереднє перетворення (див. Приклад 10(з)).

У ряді випадків для знаходження похідної доцільно задану функцію спочатку прологарифмувати (найчастіше мається на увазі натуральний логарифм). Потім знайти похідну від цього логарифма і по ній відшукати похідну від заданої функції. Такий прийом називається логарифмічним диференціюванням.

Метод логарифмічного диференціювання дозволяє легко знаходити похідні показово-ступеневих функцій виду

,

де й – диференційовні функції аргументу .

Приклад 14.

Знайти похідну функції .

Розв’язок.

Прологарифмуємо обидві частини функції й перетворимо вираз:

.

Тепер диференціюємо рівняння, як неявно задану функцію:

;

;

;

;

Оскільки , то остаточно отримуємо:

.

Похідні вищих порядків

Похідною 2-го порядку від функції називається похідна від її першої похідної, тобто:

.

Аналогічно, похідною 3-го порядку від функції називається похідна від її другої похідної, тобто:

.

Таким чином, похідною -го порядку від функції називається похідна від похідної -го порядку, тобто:

.

Отже, для знаходження похідної -го порядку необхідно послідовно знаходити похідну першого, потім другого, потім третього і т.д. до-го порядку.

Приклад 15.

Знайти третю похідну функції .

Розв’язок.

;

;

.

2.3. Диференціал функції

Із визначення похідної і властивостей границі випливає, що якщо

то ,

де – нескінченно мала величина ().

Виражаємо і отримуємо, що:

.

Оскільки , то надалі частину приросту функціїможна не враховувати і ми одержимо:

Основна частина приросту функції, лінійна щодо приросту незалежної змінної , називається диференціалом функції і позначаєтьсяабо:

.

Оскільки диференціал , то диференціал функції дорівнює добутку похідної функції на диференціал аргументу:

.

Таким чином, для знаходження диференціала функції, необхідно знайти її похідну і помножити її на диференціал незалежної змінної .

Приклад 16.

Знайти диференціал функції .

Розв’язок.

.

2.4. Застосування диференціального числення функції однієї змінної

2.4.1. Застосування похідної при обчисленні границь.

Правило Лопіталя

При обчисленні границі функції підстановка граничного значення аргументу часто приводить до невизначеностей виду ,, від яких неможливо позбутися за допомогою раніше вивчених прийомів. Теорема, відома за назвоюправило Лопіталя, є одним із основних інструментів для розкриття таких невизначеностей.

Правило Лопіталя: Нехай у деякому околі точки функціїідиференційовні та. Якщоіодночасно є нескінченно малими або нескінченно великими функціями при , тоді

,

за умови, що границя відношення похідних існує.

Ця теорема справедлива також і для односторонніх границь, і у випадку, коли .

У деяких випадках розкриття невизначеностей виду можлива необхідність кількаразового застосування правила Лопіталя.

Невизначеності ,,,,, зводяться до невизначеностей виду шляхом алгебраїчних перетворень.

Приклад 17.

Обчислити за допомогою правила Лопіталя границі:

а) ; б); в).

Розв’язок.

а)

.

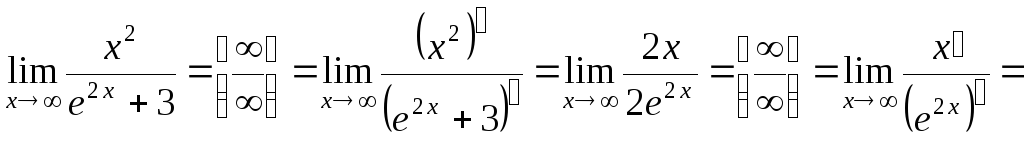
б)

.

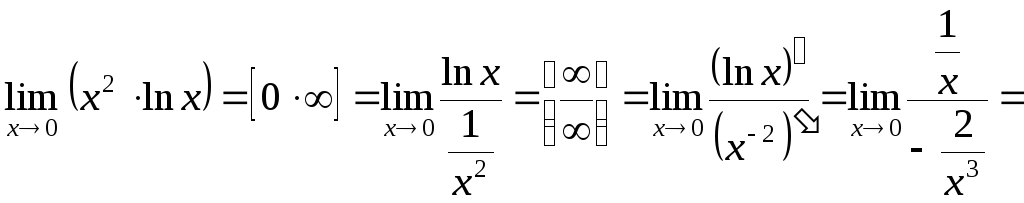
в) .

Позначимо границю через і прологарифмуємо вираз:

;

або .

Тоді:

.

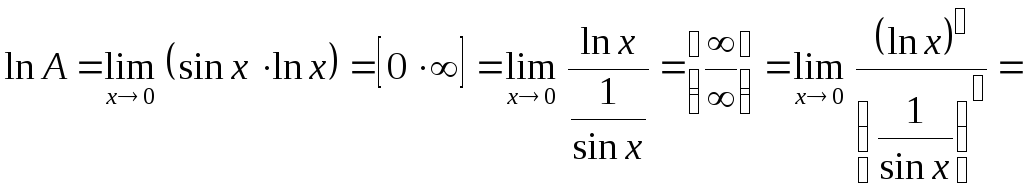
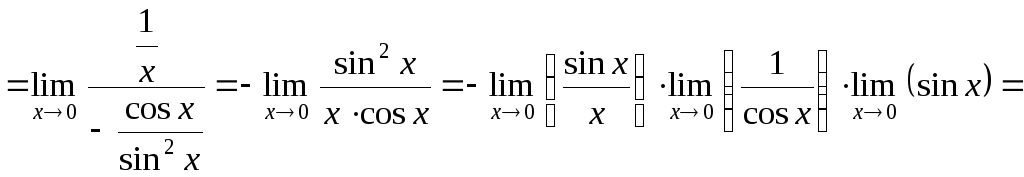
Оскільки , то границя, яку ми знаходили, дорівнює:

.