3.2.2. Властивості визначеного інтегралу

1. Довільний постійний множник можна виносити за знак інтегралу:

, де .

2. Інтеграл від алгебраїчної суми інтегрованих функцій дорівнює алгебраїчної сумі інтегралів від цих функцій:

.

3. При перестановці меж інтегрування визначений інтеграл змінює свій знак на протилежний:

.

Зауваження. Якщо межі інтегрування рівні між собою , то

.

4. Інтеграл на всьому відрізку дорівнює сумі інтегралів на частинах цього відрізка:

,

5. Значення визначеного інтеграла не залежить від позначення змінної інтегрування, тобто:

.

6. «Теорема про середнє»: Якщо функція неперервна на відрізку , то існує точка така, що

.

7. Нерівність між неперервними на відрізку функціями можна інтегрувати. Так, якщо при, то

.

8. Інтеграл можна оцінити найменшим значенням функції і найбільшим значенням функціїна відрізку :

.

3.2.3. Обчислення визначеного інтеграла

При обчисленні визначених інтегралів застосовують ті ж методи, що і для невизначених інтегралів, а саме: безпосереднє інтегрування, метод заміни змінної (метод підстановки) і метод інтегрування частинами.

Метод заміни змінної в визначеному інтегралі

Якщо для неперервної підінтегральної функції неможливо знайти первіснубезпосереднім інтегруванням, то для обчислення визначеного інтегралазастосовують заміну змінної. У результаті інтеграл приводиться до табличного і обчислюється за формулою Ньютона-Лейбніца. Межі інтегрування змінюються у відповідність із обраною підстановкою.

Якщо функція і її похідна неперервні на відрізку і при цьому ,, то справедлива рівність:

.

Дана формула описує метод підстановки в визначеному інтегралі.

Зауваження: При обчисленні визначеного інтеграла методом підстановки повертатися до старої змінної не потрібно, тому що межі інтегрування в визначеному інтегралі змінюються відповідно до нової змінної.

Приклад 39.

Обчислити визначені інтеграли методом підстановки:

а) ;б) ; в).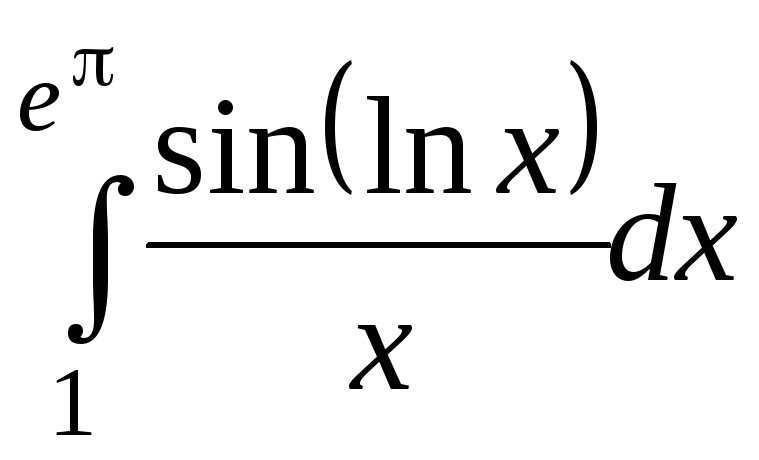

Розв’язок.

а)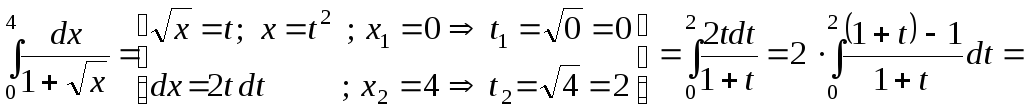

.

б)

.

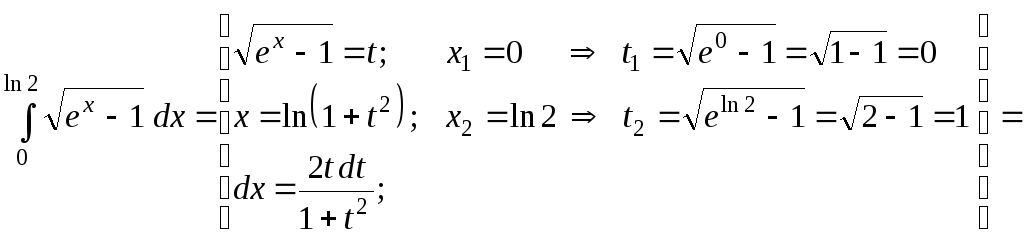
в)

.

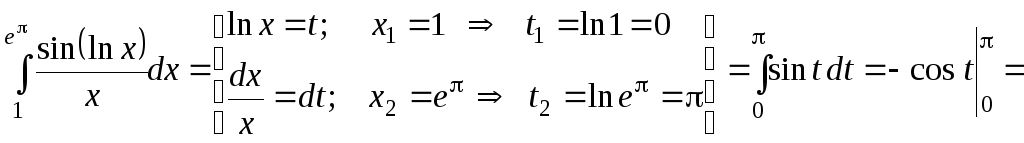
Метод інтегрування частинами у визначеному інтегралі

Якщо функції імають неперервні похідні на відрізку , то формула інтегрування частинами має вигляд:

.

Приклад 40.

Обчислити визначені інтеграли методом інтегрування частинами:

а) ; б).

Розв’язок.

а)

.

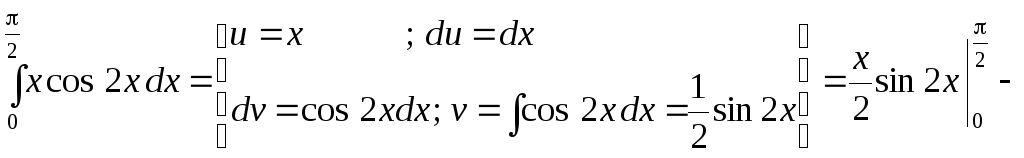
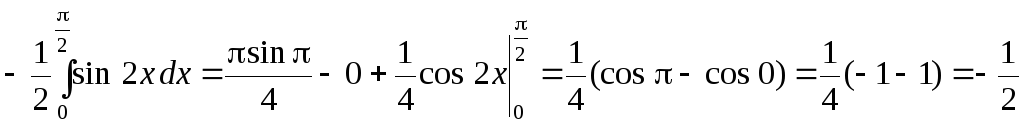б)

.

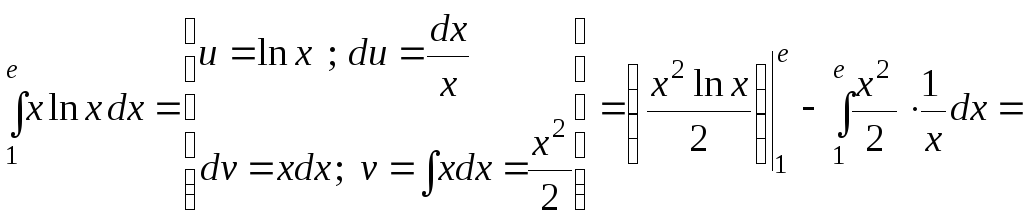
3.2.4. Невласні інтеграли

Визначений інтеграл , у якому проміжок інтегрування– скінченний, а підінтегральна функція– неперервна на відрізку , називаєтьсявласним інтегралом.

Невласним інтегралом називається визначений інтеграл від неперервної функції, але з нескінченним проміжком інтегрування або визначений інтеграл з скінченним проміжком інтегрування, але від функції, що має на ньому нескінченний розрив. Відповідно, розрізняють невласні інтеграли I роду (з нескінченними межами) і II роду (інтеграл від розривної функції).

Невласним інтегралом першого роду неперервної на інтерваліфункціїназивається скінченна границя.

Таким чином, за визначенням:

.

Якщо границя, яка знаходиться в правій частині рівності існує і скінченна, то невласний інтеграл збігається, у противному випадку – розбігається.

Аналогічно визначається невласний інтеграл на інтервалі :

.

Невласний інтеграл із двома нескінченними межами (на інтервалі ) розбивається на два за формулою:

, де – довільне число.

Такий інтеграл збігається лише тоді, коли збігаються обидва інтеграли на які він розбивається.

Приклад 41.

Обчислити невласні інтеграли І роду: а) ; б).

Розв’язок.

а) .

Оскільки границя – скінченна, то невласний інтеграл збігається.

б) .

Оскільки границя - нескінченна, то невласний інтеграл розбігається.

Невласним інтегралом другого роду неперервної на інтерваліфункції, що має нескінченний розрив при, називається скінченна границя. Таким чином, за визначенням:

.

Якщо границя, яка знаходиться в правій частині рівності існує і скінченна, то невласний інтеграл збігається, у противному випадку – розбігається.

Аналогічно, якщо функція , неперервна на інтервалі, має нескінченний розрив при, то невласний інтеграл другого роду визначається за формулою:

.

Якщо функція має нескінченний розрив у внутрішній точцівідрізка, то невласний інтеграл другого роду визначаєтьсяза формулою:

.

Такий інтеграл збігається лише тоді, коли збігаються обидва інтеграли на які він розбивається.

Приклад 42.

Обчислити невласний інтеграл ІІ роду .

Розв’язок.

Підінтегральна функція має нескінченний розрив на лівій межі проміжку інтегрування , оскільки дана функція не визначена приі. Тоді:

.

Оскільки границя – нескінченна, то невласний інтеграл розбігається.