
- •Вища математика математичний аналіз функцій однієї змінної
- •0501 „Економіка і підприємництво”,
- •0502 „Менеджмент”
- •Видання розглянуто і рекомендовано до друку на засіданні кафедри фізико-математичних дисциплін (протокол № 5 від 13 січня 2009 р.);
- •Скорочені теоретичні відомості
- •1. Границі і неперервність функції
- •Границя числової послідовності і функції в точці і на нескінченності. Односторонні границі функції в точці.
- •1.2. Основні теореми про границі
- •1.3. Нескінченно малі і нескінченно великі функції
- •1.4. Приклади обчислення границь
- •1.5. Неперервність функції
- •Питання для самоперевірки
- •2. Диференціальне числення функції однієї змінної
- •2.1. Похідна функції. Геометричний зміст похідної функції
- •2.2. Основні правила диференціювання функції. Таблиця похідних
- •Таблиця похідних основних елементарних функцій
- •Основні правила диференціювання
- •Похідна складної функції
- •Зведена таблиця формул диференціювання
- •Похідна оберненої функції
- •Диференціювання функцій, заданих параметрично
- •Диференціювання неявної функції
- •Логарифмічне диференціювання
- •Похідні вищих порядків
- •2.3. Диференціал функції
- •2.4. Застосування диференціального числення функції однієї змінної
- •2.4.1. Застосування похідної при обчисленні границь.
- •Правило Лопіталя
- •2.4.2. Зростання і спадання функції на інтервалі
- •2.4.3. Екстремуми функції
- •2.4.4. Найбільше і найменше значення функції на відрізку.
- •Значень функції на відрізку:
- •2.4.5. Опуклість графіка функції. Точки перегину
- •Проміжки опуклості, вгнутості й точки перегину:
- •2.4.6. Асимптоти графіка функції
- •2.4.7. Повне дослідження функції і побудова її графіка
- •2.5. Питання для самоперевірки
- •3. Інтегральне числення функції однієї змінної
- •3.1. Невизначений інтеграл
- •3.1.1 Властивості невизначеного інтеграла.
- •3.1.2. Таблиця невизначених інтегралів
- •3.1.3. Основні методи інтегрування
- •Метод безпосереднього інтегрування
- •Метод заміни змінної
- •Метод інтегрування частинами
- •3.1.4. Інтегрування дрібно-раціональних функцій
- •Інтегрування найпростіших дробів
- •3.1.5. Інтегрування тригонометричних функцій
- •, , .
- •3.1.6. Інтегрування деяких видів ірраціональних функцій
- •3.1.7. Інтегрування диференціального бінома
- •3.1.8. Інтеграли, що не виражаються через елементарні функції
- •3.1.9. Питання для самоперевірки
- •3.2. Визначений інтеграл
- •3.2.1. Інтегральна сума і визначений інтеграл
- •3.2.2. Властивості визначеного інтегралу
- •3.2.3. Обчислення визначеного інтеграла
- •Метод заміни змінної в визначеному інтегралі
- •Метод інтегрування частинами у визначеному інтегралі
- •3.2.4. Невласні інтеграли
- •3.2.5. Геометричні застосування визначеного інтеграла
- •Обчислення площ плоских фігур у декартових координатах
- •Обчислення об'єму тіла обертання
- •Обчислення довжини дуги кривої
- •3.2.6. Питання для самоперевірки
- •Література
- •Индивидуальні завдання до розрахунково-графічної роботи
- •4) ; 5).
- •Таблиці вибору варіантів завдань для ргр № 2
- •211 Група
- •212 Група
- •213 Група
- •214 Група
- •215 Група
- •311 Група
- •312 Група
- •313 Група
- •314 Група
- •315 Група
- •316 Група
- •1111 Група
- •1112 Група
- •1211 Група
- •1212 Група
- •1311 Група
- •1312 Група
- •1313 Група
- •1511 Група
- •1512 Група
1.3. Нескінченно малі і нескінченно великі функції
Функція
![]() називаєтьсянескінченно
малою при
називаєтьсянескінченно
малою при
![]() ,
якщо
,
якщо
![]() .
.
За
визначенням границі функції рівність
![]() означає, що для заданого завгодно малого
числа
означає, що для заданого завгодно малого
числа
![]() знайдеться таке число
знайдеться таке число![]() ,
що для всіх
,
що для всіх![]() ,
що задовольняють нерівності
,
що задовольняють нерівності![]() ,
буде виконуватися нерівність
,
буде виконуватися нерівність![]() .
.
Функція
![]() називаєтьсянескінченно
великою при
називаєтьсянескінченно
великою при
![]() ,
якщо
,
якщо
![]() .
.
За
визначенням границі функції рівність
![]() означає, що для заданого завгодно
великого числа
означає, що для заданого завгодно
великого числа
![]() знайдеться таке число
знайдеться таке число
![]() ,
що для всіх
,
що для всіх![]() ,
що задовольняють нерівності
,
що задовольняють нерівності![]() ,
буде виконуватися нерівність
,
буде виконуватися нерівність![]() .
.
Зауваження:
Аналогічно, можна говорити про нескінченно
великі і нескінченно малі функції при
![]() .
.
Нескінченно великі і нескінченно малі функції мають наступні властивості.
Властивість 1. Сума скінченної кількості нескінченно малих функцій є функцією нескінченно малою.
Властивість 2. Добуток обмеженої функції на нескінченно малу функцію є функцією нескінченно малою.
Властивість 3. Добуток постійної на нескінченно малу функцію є функцією нескінченно малою.
Властивість 4. Добуток скінченної кількості нескінченно малих функцій є функцією нескінченно малою.
Властивість 5. Сума скінченної кількості нескінченно великих функцій є функцією нескінченно великою.
Властивість 6. Добуток обмеженої функції на нескінченно велику функцію є функцією нескінченно великою.
Властивість 7. Добуток постійної на нескінченно велику функцію є функцією нескінченно великою.
Властивість 8. Функція, обернена за величиною нескінченно великий, є функцією нескінченно малою
Властивість 9. Функція, обернена за величиною нескінченно малій, є функцією нескінченно великою.
Зауваження: властивості 8 й 9 відображають зв'язок між нескінченно великою і нескінченно малою функціями.
Якщо
прийняти наступні позначення: нескінченно
мала функція – символ 0, нескінченно
велика функція – символ ,
постійна величина – символ
![]() ,
обмежена функція – символ
,
обмежена функція – символ![]() ,
то всі викладені властивості можна
записати в такий спосіб:
,
то всі викладені властивості можна
записати в такий спосіб:
1.
![]() ;
4.
;
4.![]() ; 7.
; 7.![]() ;
;
2.
![]() ; 5.
; 5.![]() ; 8.
; 8.![]() ;
;
3.
![]() ; 6.
; 6.![]() ; 9.
; 9.![]()
Для
порівняння двох нескінченно малих
функцій
![]() і
і![]() при
при
![]() знаходять
границю їх відношення:
знаходять
границю їх відношення:
![]()
Якщо
 ,
то
,
то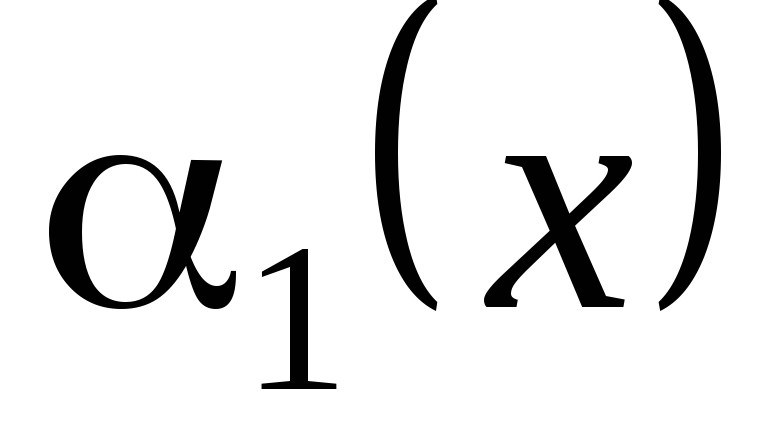 називається нескінченно малою функцією
більш високого порядку в порівнянні
із
називається нескінченно малою функцією
більш високого порядку в порівнянні
із
Якщо
 то
то називається нескінченно малою функцією
більш високого порядку в порівнянні
із
називається нескінченно малою функцією
більш високого порядку в порівнянні
із
Якщо
 ,
то
,
то й
й називаються нескінченно малими функціями
одного і того ж порядку.
називаються нескінченно малими функціями
одного і того ж порядку.Якщо
 ,
те
,
те
 й
й називаються еквівалентними (рівносильними)
нескінченно малими:
називаються еквівалентними (рівносильними)
нескінченно малими:

 .
.
При
обчисленні границь використовують
наступні заміни еквівалентних нескінченно
малих функцій при
![]() або
або![]() :
:
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() .
.
Варто зауважити, що границя відношення нескінченно малих функцій дорівнює границі відношення еквівалентних їм нескінченно малих функцій.
Зауваження:заміну нескінченно малих функцій на еквівалентні їм нескінченно малі функції не можна робити у випадку різниці нескінченно малих функцій.
1.4. Приклади обчислення границь
Застосовуючи
теореми про границі, а також властивості
нескінченно малих і нескінченно великих
функцій, практичне обчислення границі
функції при
![]() зводиться до підстановки замість
зводиться до підстановки замість
![]() його
граничного значення
його
граничного значення
![]() і обчисленню значення виразу. При цьому
символ
і обчисленню значення виразу. При цьому
символ
![]() не
пишеться.
не
пишеться.
Приклад 1.
Обчислити
границі: а)![]() ; б)
; б)
![]() .
.
Розв’язок.
а)
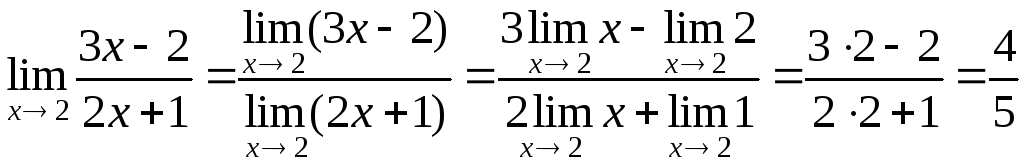 .
.
На практиці теореми про границі, властивості нескінченно малих і нескінченно великих функцій враховуються подумки, рішення оформлюється в такий спосіб:
![]() .
.
б)
![]() .
.
Якщо
в результаті підстановки замість
![]() його
граничного значення
його
граничного значення
![]() неможливо судити про результат, говорять,
що має місце невизначеність і для
обчислення границі необхідне перетворення
функції – говорять, що потрібно “позбутися
від невизначеності” або “розкрити
невизначеність”.
неможливо судити про результат, говорять,
що має місце невизначеність і для
обчислення границі необхідне перетворення
функції – говорять, що потрібно “позбутися
від невизначеності” або “розкрити
невизначеність”.
До основних невизначеностей відносять наступні випадки, отримані в результаті підстановки:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Залежно від виду невизначеності і виду функції, границю якої знаходять, застосовують різні підходи для її розкриття.
Наприклад,
якщо невизначеність
![]() отримана при обчисленні границі
дробово-раціональної функції (відношення
двох многочленів) при
отримана при обчисленні границі
дробово-раціональної функції (відношення
двох многочленів) при
![]() ,
то
для
розкриття невизначеності необхідно
розкласти на множники чисельник і
знаменник дробу і скоротити дріб на
загальний множник
,
то
для
розкриття невизначеності необхідно
розкласти на множники чисельник і
знаменник дробу і скоротити дріб на
загальний множник
![]() .
На етапі скорочення відбувається
розкриття невизначеності.
.
На етапі скорочення відбувається
розкриття невизначеності.
Приклад 2.
Обчислити
границю
![]() .
.
Розв’язок.
Оскільки
при безпосередній підстановці замість
![]() граничного значення
граничного значення
![]() отримують невизначеність
отримують невизначеність![]() і функція дробово-раціональна, розкладемо
на множники чисельник і знаменник.
і функція дробово-раціональна, розкладемо
на множники чисельник і знаменник.
![]()
![]()
D = (–1)2 – 4·1·(–6) = 1 + 24 = 25 D = 12 – 4·2·(–21) = 1 + 168 = 169
![]() ;
;
![]() .
.![]() ;
;![]() .
.
Тоді
![]() . Тоді
. Тоді
![]() .
.
Підставимо замість многочленів їх розкладення на множники й отримаємо:
 .
.
Якщо
невизначеність
![]() отримана при обчисленні границі
дробово-ірраціональної функції при
отримана при обчисленні границі
дробово-ірраціональної функції при
![]() ,
то щоб виділити загальний множник
чисельника і знаменника
,
то щоб виділити загальний множник
чисельника і знаменника
![]() ,
а потім скоротити дріб, необхідно
помножити чисельник і знаменник на
сполучений вираз для випадку квадратного
кореня та на неповний квадрат суми або
різниці для випадку кубічного кореня.
,
а потім скоротити дріб, необхідно
помножити чисельник і знаменник на
сполучений вираз для випадку квадратного
кореня та на неповний квадрат суми або
різниці для випадку кубічного кореня.
Приклад 3.
Обчислити
границі: а)
![]() ;
б)
;
б)
![]() .
.
Розв’язок.
а)
Оскільки при безпосередній підстановці
![]() у функцію отримують невизначеність
виду
у функцію отримують невизначеність
виду
![]() ,
функція
дробово-ірраціональна і містить корінь
квадратний, то для розкриття невизначеності
помножимо чисельник і знаменник на
вираз, сполучений чисельнику, і
скористаємося формулою
,
функція
дробово-ірраціональна і містить корінь
квадратний, то для розкриття невизначеності
помножимо чисельник і знаменник на
вираз, сполучений чисельнику, і
скористаємося формулою
![]() .
.
![]()
=![]()
=![]()
=![]() .
.
б)
Оскільки при безпосередній підстановці
![]() у функцію отримують невизначеність
виду
у функцію отримують невизначеність
виду
![]() ,
функція
дробово-ірраціональна і містить корінь
кубічний, то для розкриття невизначеності
помножимо чисельник і знаменник на
неповний квадрат суми для виразу в
знаменнику і скористаємося формулою
,
функція
дробово-ірраціональна і містить корінь
кубічний, то для розкриття невизначеності
помножимо чисельник і знаменник на
неповний квадрат суми для виразу в
знаменнику і скористаємося формулою
![]() .
.

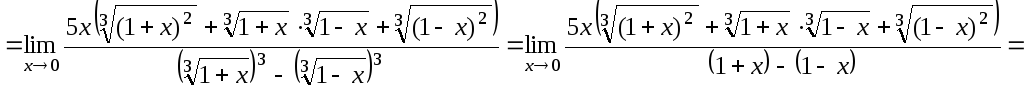
![]()
![]() .
.
Для
розкриття невизначеності
![]() одержуваної при обчисленні границі
дробово-раціональної функції при
одержуваної при обчисленні границі
дробово-раціональної функції при![]() ,
застосовують прийом винесення аргументу
,
застосовують прийом винесення аргументу
![]() найбільшого степеня (чисельника або
знаменника) за дужки в чисельнику і
знаменнику та його наступне скорочення.
найбільшого степеня (чисельника або
знаменника) за дужки в чисельнику і
знаменнику та його наступне скорочення.
Приклад 4.
Обчислити
границі: а)
![]() ;
б)
;
б)
![]() .
.
Розв’язок.
а)
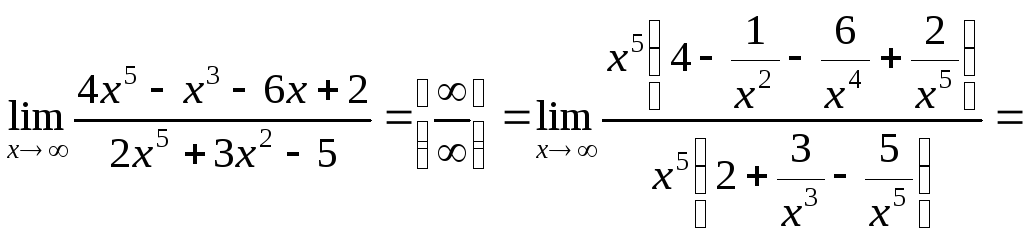
 .
.
б)

= .
.
Якщо
під знаком границі містяться тригонометричні
функції, то невизначеність
![]() розкривається за допомогою перетворень,
що приводять до скорочення дробу та
зведення отриманого виразу до першої
визначної границі або її наслідків.
розкривається за допомогою перетворень,
що приводять до скорочення дробу та
зведення отриманого виразу до першої
визначної границі або її наслідків.
Приклад 5.
Обчислити
границю
![]() .
.
Розв’язок.
Перший спосіб.
Помножимо
чисельник і знаменник дробу на
![]() і
і![]() та скористаємося першою стандартною
границею і її наслідками.
та скористаємося першою стандартною
границею і її наслідками.
![]()
=![]() .
.
Другий спосіб.
Цю ж границю можна обчислити, використовуючи еквівалентності нескінченно малих тригонометричних функцій.
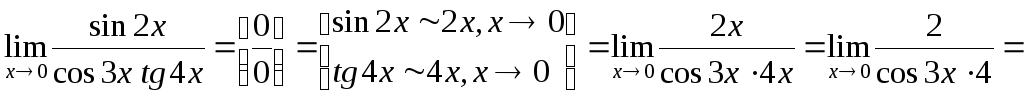
![]()
Невизначеність
виду
![]() розкривається зведенням до другої
визначної границі.
розкривається зведенням до другої
визначної границі.
Приклад 6.
Обчислити
границю
![]() .
.
Розв’язок.
Оскільки
при безпосередній підстановці
![]() отримуємо невизначеність виду
отримуємо невизначеність виду
![]() ,
скористаємося наслідком із другої
визначної границі, попередньо перетворивши
функцію.
,
скористаємося наслідком із другої
визначної границі, попередньо перетворивши
функцію.

 .
.
Невизначеність
виду
![]() може зводитися до невизначеності виду
може зводитися до невизначеності виду
![]() за допомогою перетворень. Далі
застосовується прийом розкриття
невизначеності виду
за допомогою перетворень. Далі
застосовується прийом розкриття
невизначеності виду![]() .
.
Приклад 7.
Обчислити
границю
![]() .
.
Розв’язок.
Підставимо
замість
![]() граничне
значення:
граничне
значення:
 .
.
Для розкриття даної невизначеності перетворимо вираз у дужках – виділимо цілу частину.
![]()
![]()
 .
.
Невизначеності
![]() ,
,![]() і
і![]() зводять до виду
зводять до виду![]() або
або![]() за допомогою перетворення функції до
дробу.
за допомогою перетворення функції до
дробу.
Приклад 8.
Обчислити
границі: а)
![]() ;
б)
;
б)
![]() .
.
Розв’язок.
а)

![]() .
.
б)


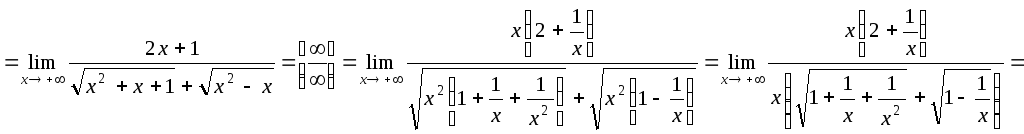
 .
.
