3.2.5. Геометричні застосування визначеного інтеграла

Основними геометричними застосуваннями визначеного інтеграла є: обчислення площі плоскої фігури, обчислення об'ємів тіл обертання навколо осей координат і обчислення довжини дуги плоскої кривої.

Обчислення площ плоских фігур у декартових координатах

Площа плоскої фігури, обмеженої неперервною на відрізку кривою , віссю , а також вертикальними прямими і (площа криволінійної трапеції – Рис. 12), визначається за формулою:

.

Якщо графік функції розташовано нижче осі (Рис. 13), то площа фігури визначається за формулою:

.

Площа фігури, обмеженої кривими і , прямими і, за умови, що (Рис. 14), визначається за формулою:

.

Зауваження: Якщо плоска фігура має складну форму, то прямими, паралельними осі , її варто розбити на частині таким чином, щоб можна було застосовувати вже відомі формули.

Приклад 43.

Обчислити площу фігур, обмежених лініями:

а) ; б).

Розв’язок.

а)

Фігура обмежена віссю () і параболою на відрізку .

Побудуємо параболу. Знайдемо точки перетину параболи з віссю . Для цього дорівняємо :

; ;;.

Знайдемо координати вершини параболи:

,

.

Парабола має вершину в точці з координатами і гілки її спрямовано вгору.

Фігура, обмежена заданими лініями зображена на рис. 15.

Площа шуканої фігури дорівнює сумі площ двох криволінійних трапецій:

.

Знайдемо площу:

(од.²)

(од.²)

Тоді площа заданої плоскої фігури дорівнює:

(од.²).

б)

Фігура обмежена параболою і прямою .

Побудуємо дані параболу і пряму (рис. 16).

Знайдемо межі інтегрування, тобто точки перетину прямої і параболи. Для цього розв’яжемо систему, складену з рівнянь цих ліній:

; ;

;

;

;

.

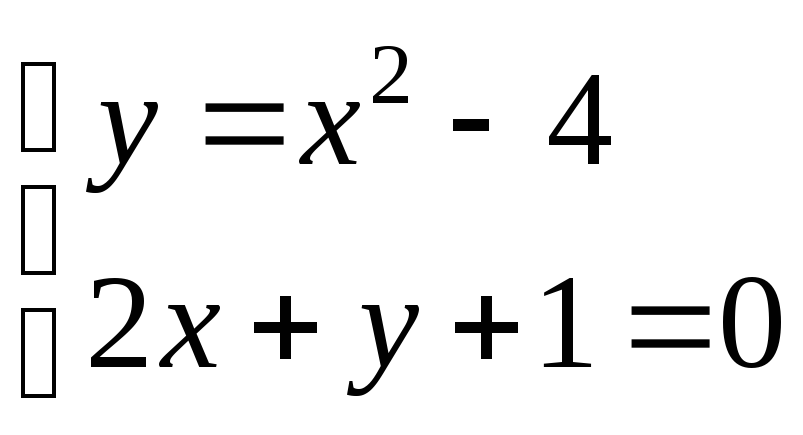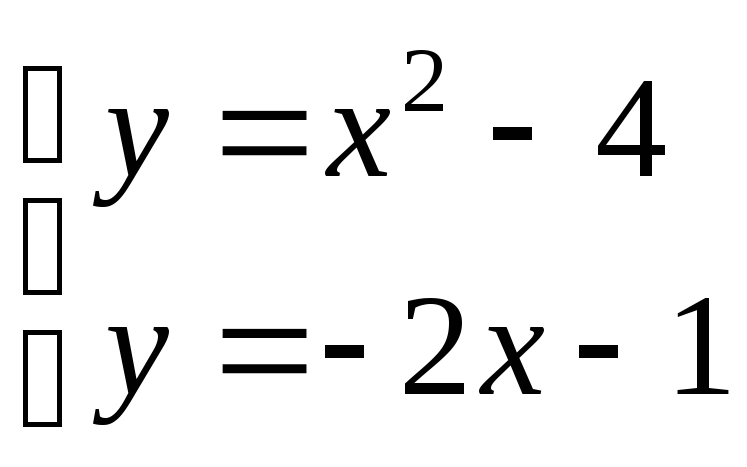Отже, парабола і пряма перетинаються в точках з абсцисами і.

Площу фігури визначаємо за формулою:

,

де лінією є пряма(обмежує фігуру зверху), алінією є парабола (обмежує фігуру знизу).

(од.²).

Обчислення об'єму тіла обертання

Тілом обертання навколо осі Ох називається фігура, отримана від обертання навколо осі криволінійної трапеції, обмеженої графіком неперервної на відрізку кривої і прямими , і (Рис.17).

Об'єм тіла обертання навколо осі визначається за формулою:

.

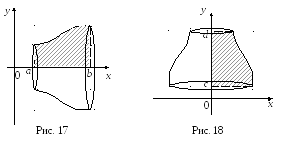
Тілом обертання навколо осі називається фігура, отримана від обертання навколо осі криволінійної трапеції, обмеженої графіком неперервної на відрізку кривої і прямими , і (рис.18).

Об'єм тіла обертання навколо осі визначається за формулою:

.

Приклад 44.

Обчислити об’єм тіла обертання.

а) Обчислити об’єм тіла утвореного обертанням навколо осі фігури, обмеженої лініями .

Розв’язок.

Побудуємо плоску фігуру, обмежену параболою (гілки спрямовані вправо)і вертикальними прямими , а також тіло, утворене обертанням навколо осі цієї плоскої фігури (рис. 19).

Визначимо об'єм тіла обертання, підставивши функцію у формулу для знаходження об'єму тіла обертання навколо осі :

(од.³⁾.

б) Обчислити об'єм тіла, утвореного обертанням навколо осі фігури, обмеженої лініями .

Рішення.

Побудуємо плоску фігуру, обмежену гіперболою і горизонтальними прямими , а також тіло, утворене обертанням навколо осі цієї плоскої фігури (рис. 20).

Визначимо об'єм тіла обертання, підставивши функцію у формулу для знаходження об'єму тіла обертання навколо осі :

(од.³⁾.