3.1.5. Інтегрування тригонометричних функцій

Розглянемо основні види інтегралів, підінтегральна функція в яких містить тригонометричні функції.

I. Інтеграли виду , деі– цілі числа.

Виділимо тут три випадки, що мають важливе значення.

1) Якщо обидва показники степеня і– парні невід’ємні числа, то необхідно перетворити підінтегральну функцію за допомогою формул зниження степеня:

2) Якщо хоча б один з показників степеня або(або ій) непарне число, то інтеграл функції знаходять шляхом відділення від неї одного множника і застосування формули:

,

і наступної підстановки:

– якщо – непарне додатне число, то;

– якщо – непарне додатне число, то.

3) Якщо обидва показники степеня і– парні і хоча б один з них від’ємний, то застосовують заміну змінної або . При цьому можуть застосовуватися формули:

.

Приклад 29.

Знайти інтеграли:

а) ; б); в); г).

Розв’язок.

а)

У цьому випадку показники: – парні додатні числа. Застосуємо формулу зниження степеня:

б)

У цьому випадку показники: ,– непарне число. Відокремимо від непарного степеня один множник першого степеня, скористаємося тотожністюі зробимо підстановку

в)

У цьому випадку показники: – непарне число, а. Відокремимо від непарного степеня один множник першого степеня, скористаємося тотожністю і зробимо підстановку

.

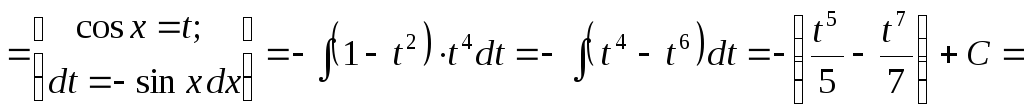
г) .

У цьому випадку показники: – парні, але– від’ємне число. Перетворимо підінтегральну функцію, скористаємося тотожністюі застосуємо підстановку .

II. Інтеграли виду деR – раціональна функція від тригонометричних функцій, знаходять за допомогою універсальної тригонометричної підстановки: . Тоді:

Приклад 30.

Знайти інтеграл

Розв’язок.

Застосовуємо універсальну тригонометричну підстановку . Тоді даний інтеграл приймає вигляд:

.

У деяких випадках знаходження інтегралів видуможе бути спрощено:

– Якщо – непарна функція відносно, тобто якщото застосовується підстановка

– Якщо – непарна функція відносно, тобто якщото застосовується підстановка

– Якщо – парна функція відносноі, тобто якщо, то застосовується підстановка.

Приклад 31.

Знайти інтеграли а) ; б).

Розв’язок.

а) Підінтегральна функція непарна відносно Застосовуємо підстановку

б)

Підінтегральна функція парна відносно і. Застосовуємо підстановкуй формулу.

.

III. Інтеграли виду , ,, деі– деякі числа (коефіцієнти).

Подібні інтеграли перетворюються в табличні за допомогою перетворення добутку тригонометричних функцій у суму за формулами:

, , .

Приклад 32.

Знайти інтеграл .

Розв’язок.

.

3.1.6. Інтегрування деяких видів ірраціональних функцій

У деяких випадках інтеграли від ірраціональних функцій за допомогою відповідної підстановки зводяться до інтегралів від раціональних функцій.

І. Інтеграли виду:, де– раціональна функція.

Такі інтеграли обчислюють за допомогою підстановки , де– загальний знаменник дробів(– найменше загальне кратне чиселі).

Приклад 33.

Знайти інтеграл .

Розв’язок.

.

Ми одержали інтеграл від неправильного раціонального дробу. Розділимо чисельник на знаменник.

Тоді інтеграл прийме вигляд:

.

ІІ. Інтеграли виду обчислюють за допомогою підстановки, де – найменше загальне кратне чисел .

Приклад 34.

Знайти інтеграл .

Розв’язок.

.

ІІІ. Інтеграли виду ,,обчислюють виділенням повного квадрата під знаком радикала і заміною змінної. У якості нової змінної приймається вираз, що перебуває в дужках в квадраті, який отримали після виділення повного квадрата.

Приклад 35.

Знайти інтеграл .

Розв’язок.

Виділимо повний квадрат у виразі під знаком радикала:

.

Після виділення повного квадрата видно, що в якості нової змінної інтегрування варто вибрати вираз . Одержуємо:

.

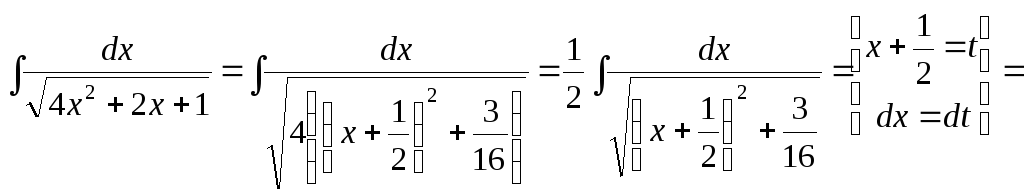
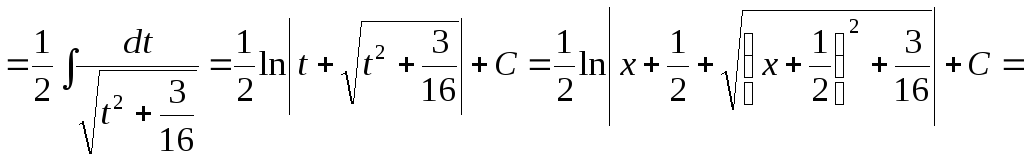
ІV. Інтеграли виду ,,приводяться до інтегралів від функцій, що раціонально залежать від тригонометричних функцій, за допомогою наступних тригонометричних підстановок:

для інтегралу :, тоді

;

для інтегралу :, тоді

для інтегралу :, тоді

Приклад 36.

Знайти інтеграли: а); б).

Розв’язок.

а)

.

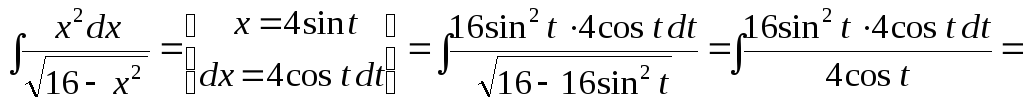
Повертаємось до старої змінної і одержимо відповідь у найбільш простому вигляді. Оскільки , то

; ;

.

Отже, остаточна відповідь має вигляд:

.

б)

.

Повертаємось до старої змінної і одержимо відповідь у найбільш простому вигляді. Оскільки , то

.

Отже, остаточна відповідь має вигляд:

.