3.1.2. Таблиця невизначених інтегралів

Оскільки інтегрування є дія обернена диференціюванню, то можна одержати таблицю основних інтегралів, застосовуючи таблицю похідних і властивості невизначеного інтеграла.

1. . 11..

2. . 12..

3. . 13..

4. . 14..

5. . 15.,.

6. . 16.,.

7. . 17.,.

8. . 18.,.

9. . 19..

10. . 20..

Якщо і– довільна функція, що має неперервну похідну, то

.

Ця властивість (її називають інваріантністю формул інтегрування) означає, що та або інша формула для невизначеного інтеграла залишається справедливою незалежно від того, змінна інтегрування – є незалежною змінною або довільною функцією від неї.

3.1.3. Основні методи інтегрування

Не існує універсального методу знаходження невизначених інтегралів. До основних методів інтегрування відносять наступні методи: безпосереднє інтегрування, метод заміни змінної (метод підстановки) і метод інтегрування частинами.

Метод безпосереднього інтегрування

Метод безпосереднього інтегрування застосовується, коли невизначений інтеграл можна знайти безпосередньо за допомогою таблиці інтегралів та властивостей невизначених інтегралів. У деяких випадках підінтегральну функцію необхідно перетворити, щоб звести поданий інтеграл до табличного інтегралу.

Зауваження: При знаходженні алгебраїчної суми інтегралів звичайно пишуть одну довільну сталу наприкінці.

Приклад 23.

Знайти інтеграли: а); б) ;

в) ; г).

Розв’язок.

а)

.

б)

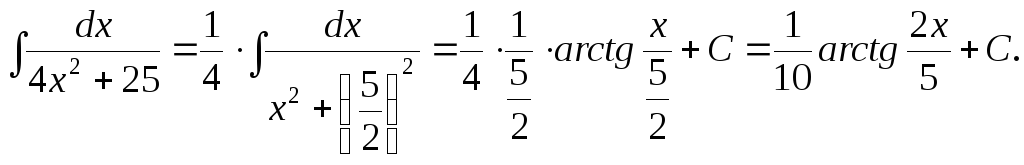
в)

=.

г)

.

Метод заміни змінної

Метод заміни змінної (метод підстановки) полягає у введенні нової змінної інтегрування (тобто підстановки) . При цьому заданий інтеграл приводиться до нового інтегралу, який повинен бути табличним або таким, що зводиться до табличного інтегралу.

Метод заміни змінної описується наступною формулою:

.

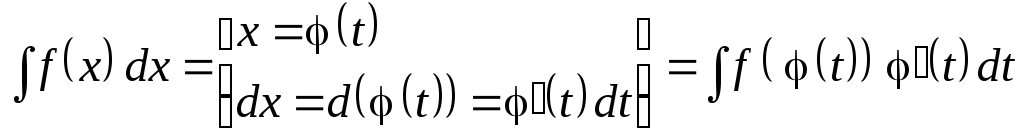Зауваження: не існує загального правила вибору підстановок. Вміння правильно підібрати підстановку визначається досвідом або виглядом підінтегральної функції.

Часто формулу заміни змінної застосовують також і у зворотному порядку: застосовують підстановку , тобто частина підінтегральної функції позначається через нову змінну. Потім із заміни виражають змінну, знаходять диференціалі підставляють усе у початковий підінтегральний вираз. Після знаходження інтеграла від нової змінноїповертаються до старої змінної. Для цього підходу справедлива формула:

.

Зауваження: якщо підінтегральний вираз містить деяку функцію та її диференціал з точністю до коефіцієнта, то виражати змінну із підстановкинеобов'язково.

Приклад 24.

Знайти інтеграли: а) ; б); в).

Розв’язок.

а)

.

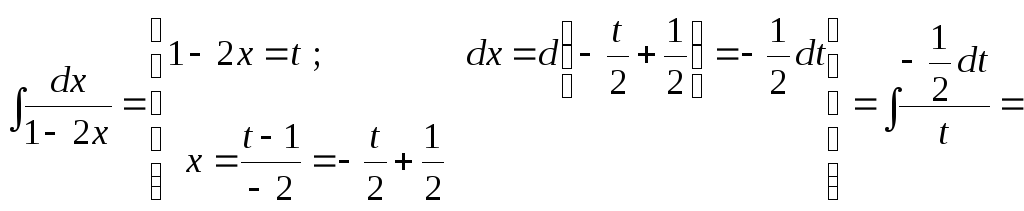
б)

.

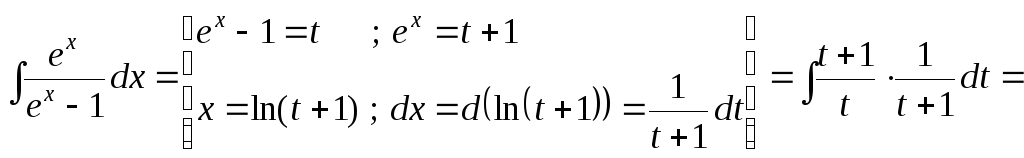
в) .

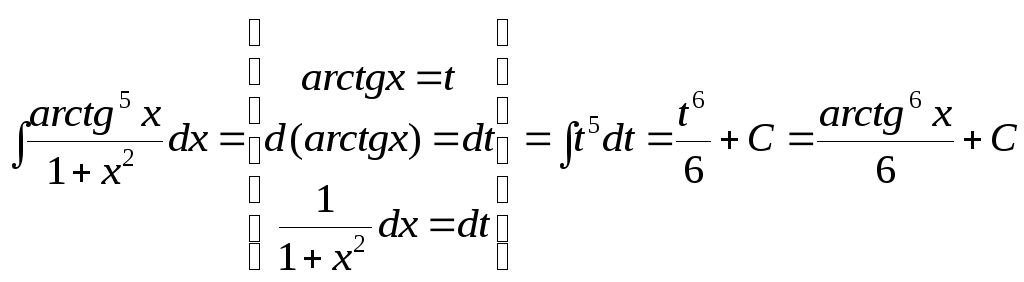Зауваження: розглянемо випадок, коли існує можливість заміни лінійного виразу , яка приводить до табличного інтеграла (див. Приклад 24а); так називану лінійну підстановку.

Якщо відома первісна для деякої функції:

,

то ,

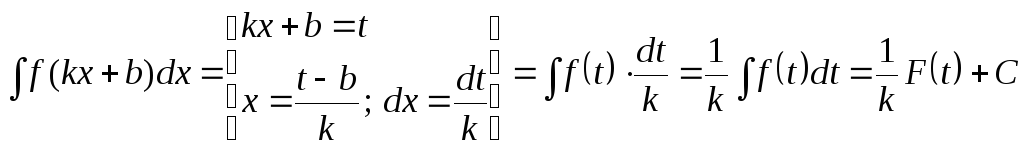тобто .

Використовуючи дане зауваження, можна розширити можливість застосування табличних інтегралів, наприклад:

;

;

;

.

Приклад 25.

Знайти інтеграли, використовуючи зауваження про лінійну підстановку:

а) ; б); в); г).

Розв’язок.

а) ;

б) ;

в) ;

г)