2.5. Питання для самоперевірки

1. Що називається похідною функції?

2. Який геометричний зміст похідної функції?

3. Який має вигляд рівняння дотичної до кривої в точці і рівняння нормалі?

4. Перелічити похідні функцій, що входять у таблицю похідних.

5. Які існують основні правила диференціювання?

6. Як знаходиться похідна складної функції?

7. Як знаходиться похідна оберненої функції?

8. Як знаходиться похідна функції, заданої параметрично?

9. Як знаходиться похідна неявної функції?

10. У чому полягає логарифмічне диференціювання?

11. Що називається диференціалом функції?

12. Як знаходиться диференціал функції?

13. У чому полягає правило Лопіталя? Для чого воно застосовується?

14. Яка функція називається зростаючою, спадаючою?

15. Сформулюйте необхідні і достатні умови зростання, спадання функції.

16. Що називається максимумом і мінімумом функції?

17. Сформулюйте необхідну і достатню умови існування екстремуму.

18. Як знаходиться найбільше і найменше значення функції на відрізку?

19. Яка функція називається опуклою, вгнутою на інтервалі?

20. Що називається точкою перегину графіка функції?

21. Сформулюйте необхідну і достатню умови існування точки перегину?

22. Що називають асимптотою графіка функції?

23. Як знайти похилу асимптоту графіка функції?

24. Викладіть схему повного дослідження функції.

3. Інтегральне числення функції однієї змінної

3.1. Невизначений інтеграл

У диференціальному численні розв’язується наступна задача: для поданої функції знайти її похідну або диференціал. Інтегральне числення розв’язує обернену задачу – знаходження самої функції за її похідною або диференціалом.

Функція називаєтьсяпервісною функцією (або просто первісною) для функції на проміжку, якщо в кожній точціцього проміжку виконується рівність:

.

Наприклад, функція є первісною функціїна усій числовій осі, тому що.

Вочевидь, що первісними будуть також будь-які функції , де– постійна, тому що.

Теорема. Якщо функція є первісною функції на інтервалі , то множина всіх первісних для визначається за формулою , де– деяка константа (довільне число).

Таким чином, невизначеним інтегралом від функції називається множина всіх її первісних:

.

Тут – знак невизначеного інтеграла,

–підінтегральна функція,

–підінтегральний вираз.

Операція знаходження невизначеного інтеграла від деякої функції називається інтегруванням цієї функції.

Геометрично невизначений інтеграл представляє собою сімейство паралельних кривих (кожному числовому значеннювідповідає певна крива сімейства).

Невизначений інтеграл існує для всякої неперервної на проміжку функції.

Правильність інтегрування завжди можна перевірити, виконавши зворотну дію, тобто знайшовши похідну функції, яку отримали в результаті інтегрування.

Похідна функції, отриманої в результаті інтегрування, повинна дорівнювати підінтегральній функції.

3.1.1 Властивості невизначеного інтеграла.

1. Похідна від невизначеного інтеграла дорівнює підінтегральній функції: .

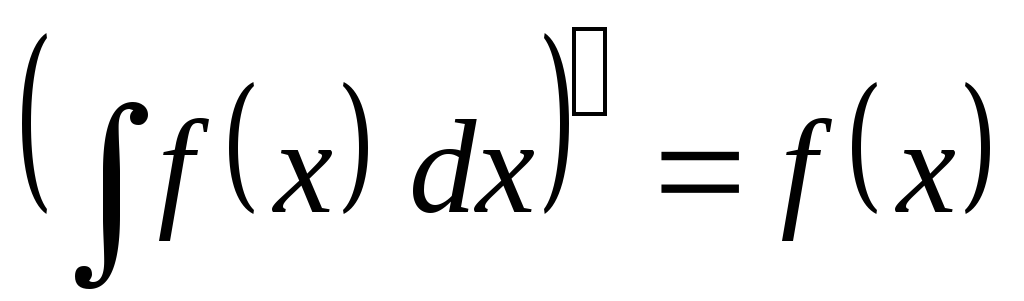2. Диференціал невизначеного інтеграла дорівнює підінтегральному виразу:

.

3. Невизначений інтеграл від диференціала деякої функції дорівнює сумі цієї функції і довільної сталої:

.

4. Постійний множник можна виносити за знак інтеграла:

.

5. Інтеграл від алгебраїчної суми двох функцій дорівнює сумі інтегралів від цих функцій:

.