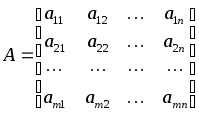Контрольные вопросы к лекции №8

1. Понятие евклидова пространства.

2. Линейная зависимость и линейная независимость векторов.

3. Понятия размерности и базиса линейного пространства.

4. Линейное преобразование векторов.

Лекция 9. Матрицы

Основные понятия:

матрица; элемент матрицы; размер матрицы; строка; столбец; квадратная матрица; главная диагональ; побочная диагональ; диагональная матрица; скалярная матрица; единичная матрица; нулевая матрица; сумма матриц; произведение матриц; согласованные матрицы; транспонирование матриц; определитель матрицы; минор; алгебраическое дополнение; линейная зависимость; линейная комбинация; ранг матрицы; окаймляющий минор; элементарные преобразования матрицы; обратная матрица.

Основные понятия

Прямоугольная таблица:

(9.1)

состоящая из строк истолбцов, называетсяматрицей размера или-матрицей.

Матрицу (9.1) будем обозначать или. Числаназываются элементами матрицы, индексобозначает номер строки, а индекс‑ номер столбца, на пересечении которых расположен элемент.

Если , то матрица (9.1) называется квадратной матрицей порядка.

В квадратной матрице -го порядка диагональ, состоящая из элементовназывается главной диагональю, состоящая из элементов‑ побочной диагональю.

Квадратная матрица:

называется диагональной. Если в диагональной матрице все диагональные элементы равны, т.е. , то такая матрица называетсяскалярной. Скалярная матрица, у которой называется единичной и обозначается буквой. Например, единичная матрица третьего порядка:

.

Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается через 0.

Матрицы иназываются равными, если их размеры одинаковы и элементы этих матриц, стоящие на одинаковых местах, равны.

Операции над матрицами

Суммой двух матриц иодинакового размера называется матрицатого же размера с элементами, равными суммам соответствующих элементов слагаемых матриц, т.е..

Сложение матриц обладает следующими свойствами:

1. Коммутативность, т.е. .

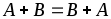2. Ассоциативность, т.е. .

3. Для любых двух матриц иодинакового размера существует единственная матрицатакая, что. Матрица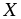обозначается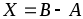и называется разностью матриц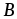и. Уравнениеимеет решение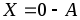, получающаяся при этом матрица называется противоположной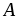и обозначается.

Произведением матрицы на числоназывается матрица, все элементы которой равны соответствующим элементам матрицы, умноженным на число.

Умножение матрицы на действительное число обладает следующими свойствами:

1. ;

2. ;

3. ;

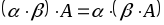4. (ассоциативность);

5. (дистрибутивность);

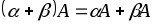6. (дистрибутивность).

Матрица называетсясогласованной с матрицей , если число столбцов матрицы равно числу строк матрицы. В этом случае произведением матрицына матрицуназывается матрица, где, т.е. элемент, стоящий в-той строке и-том столбце матрицы произведения равен сумме произведений элементов-той строки матрицына соответствующие элементы-го столбца матрицы.

Свойства умножения:

1. Если матрица согласована с матрицей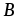, а матрицасогласована с матрицей, то‑ассоциативность умножения;

2. ‑свойство дистрибутивности;

3. Умножение матриц не коммутативно, т.е., как правило, .

Транспонированием матрицы называется операция замены местами строк и столбцов с сохранением порядка их следования, т.е. -я строка матрицыстановится-тым столбцом транспонированной матрицы. Матрица, транспонированная к матрицеобозначается.

Свойства транспонирования:

1. 

2. 

3. 

4.