Тема 3. Линейная алгебра Лекция 8. Понятие евклидова пространства

Основные понятия:

евклидово пространство; –мерный вектор; неравенство Коши-Буняковского; коллинеарные векторы; неколлинеарные векторы; сонаправленные векторы; противоположно направленные векторы; линейная комбинация векторов; линейно зависимые векторы; линейно независимые векторы; размерность линейного пространства; базис векторного пространства.

N-мерные векторы

Декартово произведение множества действительных чисел само на себя состоит из всевозможных упорядоченных числовых пар. Это множество обозначаюти его можно отождествить с плоскостью. Множествосостоит из упорядоченных троек и представляет собой трехмерное пространство. Если осуществить декартово произведениена себяраз, можно получить множество всех точек-мерного пространства. Каждый элемент пространствапредставляет собой последовательностьчисел и записывается в виде. Числоназывается первой координатой-мерного вектора,– второй координатой и т.д., а число– размерностью вектора. В ряде случаев в пространстве–мерных векторов также бывает возможно определить операцию скалярного произведения векторовичерез операции над их координатами.

В общем случае и– это–мерные векторы, т.е., и. Их скалярное произведение равно сумме попарных произведений их соответствующих координат, т.е.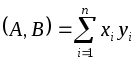. Длиной–мерного вектораназывается число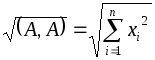. Скалярное произведениеназывается скалярным квадратом вектораи обозначается. Поскольку скалярный квадрат является суммой квадратов координат вектора, то его значение будет неотрицательным, причемтогда и только тогда, когда все координаты этого вектора равны нулю, т.е. вектор– нулевой.

Пространство –мерных векторов, в котором определена операция скалярного произведения, называетсяевклидовым пространством.

Теорема. Если и– это–мерные векторы евклидова пространства, то справедливо неравенство:

Доказательство: Рассмотрим вектор , где– любое действительное число. Поскольку, то на основании свойств скалярного произведения можно записать:

Если предположить, что , то справедливо следующее:

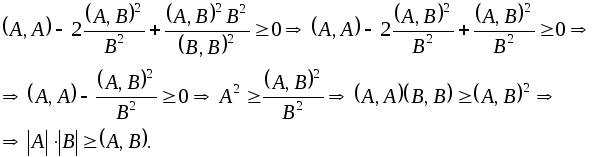
Доказанное неравенство называется неравенством Коши-Буняковского. Причем, равенство имеет место тогда и только тогда, когда векторы илинейно зависимы. В общем случае, угол между векторамииможно определить как решение уравнения:

.

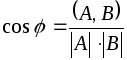Таким образом, в евклидовом пространстве –мерных векторов скалярное произведение любых двух векторовиравно:

.

Теорема. Ненулевые –мерные векторыиравны тогда и только тогда, когда угол между этими векторами равен нулю и длины их равны.

Доказательство:

Необходимость:

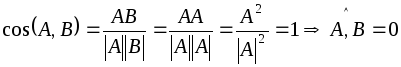
Достаточность:

Пусть и

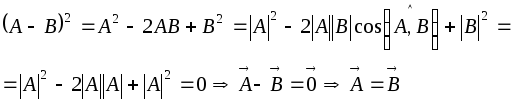
Коллинеарные векторы

Два ненулевых -мерных вектораиназываютсяколлинеарными, если угол между ними равен или.

Если , то коллинеарные векторы называютсясонаправленными или одинаково направленными .

Если , то коллинеарные векторы называютсяпротивоположно направленными .

Если условие коллинеарности между векторами ине выполняется (т.е.), то такие вектора называютсянеколлинеарными.

Теорема. Ненулевые векторы иколлинеарны тогда и только тогда, когда найдется такое ненулевое число, что.

Доказательство:

Необходимость:

1. .

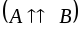
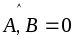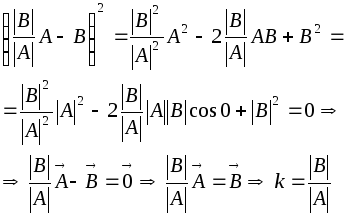
2. . Для этого случая аналогично доказывается, что , при .

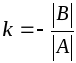Достаточность:

Число имеет только два значения:. Это означает, чтоили, соответственно. Таким образом, вектораиколлинеарны.