Задача 1

Имеются следующие данные по туристическим фирмам:

№ фирмы	Число сотрудников	Прибыль (тыс. руб.)	№ фирмы	Число сотрудников	Прибыль (тыс. руб.)
1	5	29	11	4	44
2	7	38	12	6	32
3	5	46	13	3	68
1	4	64	14	4	65
5	3	62	15	2	54
6	4	70	16	3	58
7	8	60	17	8	79
8	8	42	I8	4	85
9	6	52	19	2	34
10	2	40	20	4	97

С целью изучения зависимости прибыли туристических фирм от числа работающих сотрудников проведите аналитическую группи­ровку. По результатам аналитической группировки определите эмпирическое корреляционное отношение и коэффициент детерминации. Охарактеризуйте данную зависимость е помощью линей­ного уравнения регрессии и коэффициента корреляции. Сделайте выводы.

Решение:

Определим число групп по формуле Стерджесса:

m = 1 + 3,322lg(n) = 1 + 3,322lg(20) = 5,32 ≈ 6

Определим интервал группировки:

чел.

Выполним группировку:

Номер группы	Интервал группировки (число сотрудников, чел.)	Количество единиц совокупности	Число сотрудников, чел.	Прибыль, тыс. руб.
1	2-3	6	2	40
			2	54
			2	34
			3	62
			3	68
			3	58
2	3-4	6	4	64
			4	70
			4	44
			4	65
			4	85
			4	97
3	4-5	2	5	29
			5	46
4	5-6	2	6	52
			6	32
5	6-7	1	7	38
6	7-8	3	8	60
			8	42
			8	79

По результатам группировки можно сделать предположение об отсутствии выраженной связи между факторным и результативным признаками.

Рассчитаем внутригрупповые дисперсии результативного признака.

1-я группа:

№	у1
1	40	160,44
2	54	1,78
3	34	348,44
4	62	87,11
5	68	235,11
6	58	28,44
Итого:	316	861,33

тыс. руб.

2-я группа:

№	у2
1	64	46,69
2	70	0,69
3	44	720,03
4	65	34,03
5	85	200,69
6	97	684,69
Итого:	425	1686,83

тыс. руб.

3-я группа:

№	у3
1	29	72,25
2	46	72,25
Итого:	75	144,5

тыс. руб.

4-я группа:

№	у4
1	52	100
2	32	100
Итого:	84	200

тыс. руб.

5-я группа:

тыс. руб.

6-я группа:

№	у6
1	60	0,11
2	42	336,11
3	79	348,44
Итого:	181	684,67

Определим среднюю из внутригрупповых дисперсий:

Для определения общей дисперсии проведём в таблице расчёты:

№	у
1	40	254,4
2	54	3,8
3	34	481,8
4	62	36,6
5	68	145,2
6	58	4,2
7	64	64,8
8	70	197,4
9	44	142,8
10	65	81,9
11	85	843,9
12	97	1685,1
13	29	726,3
14	46	99
15	52	15,6
16	32	573,6
17	38	322,2
18	60	16,4
19	42	194,6
20	79	531,3
Итого:	1119	6420,95

Тогда:

Определим межгрупповую дисперсию:

Проверим правило сложения дисперсий:

Правило выполняется, следовательно, расчёты выполнены верно.

Коэффициент детерминации рассчитывается по формуле:

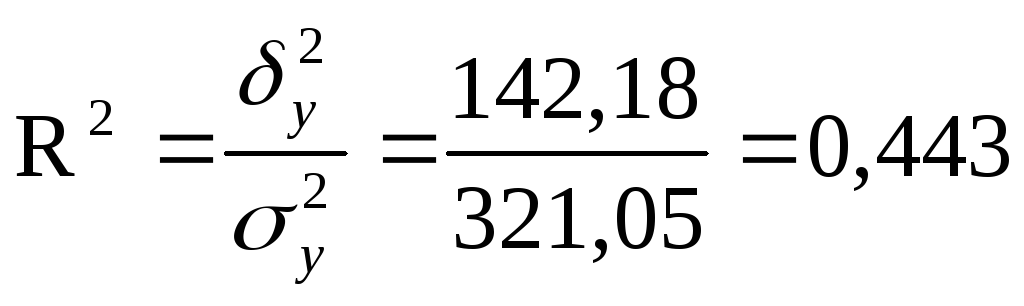
Определим эмпирическое корреляционное отношение:

Таким образом, 44,3% вариации прибыли туристических фирм объясняется вариацией количества сотрудников, а остальные 55,7% - вариацией прочих факторов.

Общий вид уравнения регрессии:

Система нормальных уравнений в общем виде:

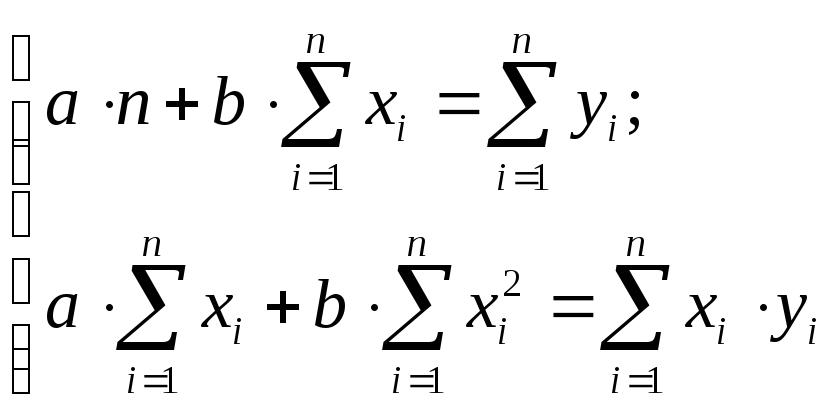
Приведём расчётную таблицу:

№	х	у		у2	ху
1	2	40	4	1600	80
2	2	54	4	2916	108
3	2	34	4	1156	68
4	3	62	9	3844	186
5	3	68	9	4624	204
6	3	58	9	3364	174
7	4	64	16	4096	256
8	4	70	16	4900	280
9	4	44	16	1936	176
10	4	65	16	4225	260
11	4	85	16	7225	340
12	4	97	16	9409	388
13	5	29	25	841	145
14	5	46	25	2116	230
15	6	52	36	2704	312
16	6	32	36	1024	192
17	7	38	49	1444	266
18	8	60	64	3600	480
19	8	42	64	1764	336
20	8	79	64	6241	632
Сумма	92	1119	498	69029	5113
Среднее	4,6	55,95	24,9	3451,45	255,65

Система нормальных уравнений с вычисленными коэффициентами

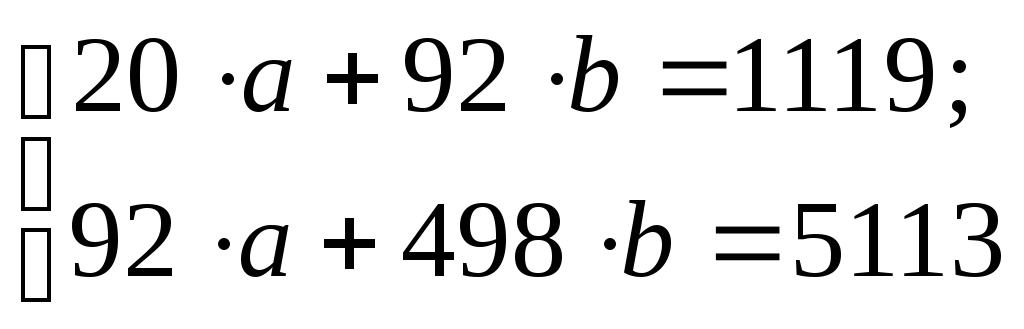
Решение системы:

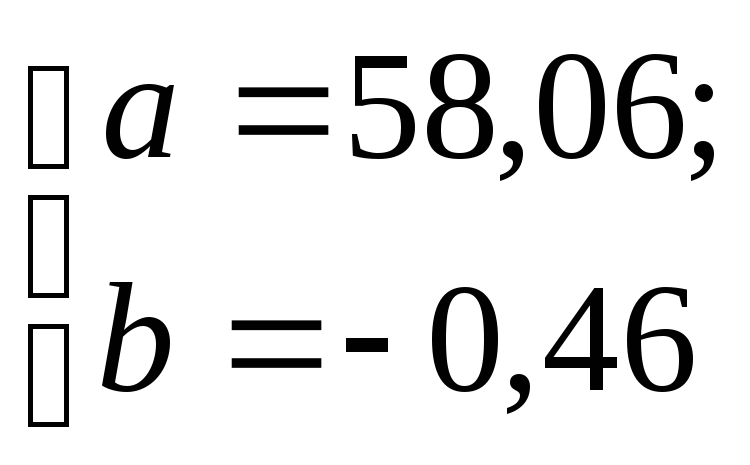
Построенное уравнение регрессии:

Коэффициент корреляции рассчитывается по формуле:

В смысле интерпретации полученных результатов регрессионного моделирования можно отметить следующее: при увеличении количества сотрудников на 1 чел. прибыль снижается в среднем на 0,46 тыс. руб. (о чём свидетельствует коэффициент регрессии);

Коэффициент корреляции показывает степень тесноты линейной связи между фактором и результатом. По шкале Чеддока значение 0,05 не попадает даже в интервал 0,1-0,3 (слабая связь), поэтому можно говорить об отсутствии значимой связи между числом сотрудников и прибылью туристической фирмы.