
- •Тема 4.Функції декількох змінних Область визначення
- •Лінії і поверхні рівня
- •Частинні похідні
- •Повний диференціал. Частинні похідні
- •Диференціювання складних функцій
- •Диференціювання функцій заданих неявно
- •Повторне диференціювання
- •Дотична площина і нормаль до поверхні
- •Екстремум функції двох змінних
- •Умовний екстремум. Найбільше та найменше значення функції в замкненій області
- •Скалярне поле. Похідна по напрямку. Градієнт.
- •Відповіді
- •4.5.. 4.7. .
Тема 4.Функції декількох змінних Область визначення
4.1. Знайти області визначення функцій:
|
1) |
|
2) |
|
|
3) |
|
4) |
|
|
5) |
|
6) |
|
|
7) |
|
8) |
|
|
9) |
|
10) |
|
|
11) |
|
12) |
|
|
13) |
|
14) |
|
|
15) |
|
16) |
|
|
17) |
|
18) |
|
|
19) |
|
20) |
|
Лінії і поверхні рівня
4.2. Знайти лінії і поверхні рівня заданих функцій:
|
1) |
|
2) |
|
|
3) |
|
4) |
|
|
5) |
|
6) |
|
|
7) |
|
8) |
|
|
9) |
|
10) |
|
|
11) |
|
12) |
|
|
13) |
|
|
|
Частинні похідні
4.3. Знайти частинні похідні заданих функцій по кожній з незалежних змінних:
|
1) |
|
2) |
|
|
3) |
|
4) |
|
|
5) |
|
6) |
|
|
7) |
|
8) |
|
|
9) |
|
10) |
|
4.4. Показати, що
функція
![]() задовольняє рівняння
задовольняє рівняння![]() .
.
4.5. Знайти
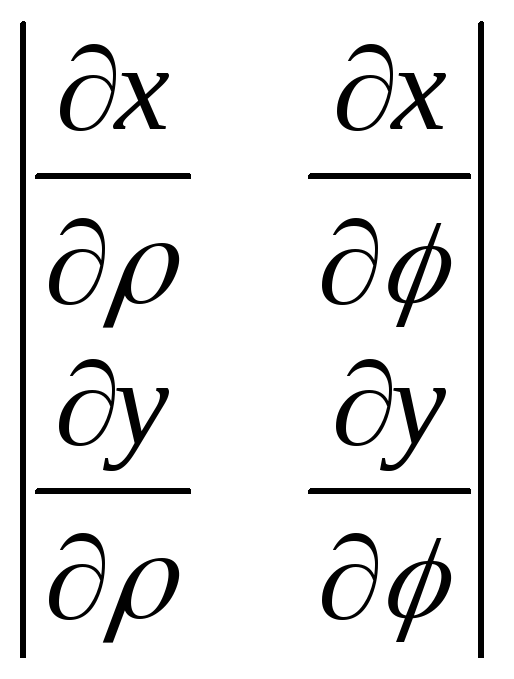 ,
якщо
,
якщо![]() ,
,![]() .
.
4.6.
Температура
![]() у даній точці
у даній точці![]() стержня
стержня![]() є функцією абсциси
є функцією абсциси![]() точки
точки![]() та часу
та часу![]() :
:![]() .
Який фізичний зміст мають частинні
похідні
.
Який фізичний зміст мають частинні
похідні
![]() та
та![]() ?
?
4.7. Сила струму згідно
з законом Ома знаходиться за формулою
![]() .
Знайти
.
Знайти![]() та
та![]() .
.
4.8. Формула Клапейрона
![]() ,
де
,
де![]() стала,
пов’язує для ідеального газу його об’єм
стала,
пов’язує для ідеального газу його об’єм![]() тиск
тиск![]() і абсолютну температуру
і абсолютну температуру![]() .
Вважаючи кожну з цих величин
.
Вважаючи кожну з цих величин![]() ,
,![]() і
і![]() функцією двох інших незалежних змінних,
визначити частинні похідні цих функцій.
Довести, що
функцією двох інших незалежних змінних,
визначити частинні похідні цих функцій.
Довести, що
![]() .
.
Повний диференціал. Частинні похідні
4.9.Знайти повні диференціали функцій:
|
1) |
|
2) |
|
|
3) |
|
4) |
|
|
5) |
|
6) |
|
4.10. Обчислити наближено приріст функції:
1)
![]() при зміні
при зміні![]() від
від![]() до
до![]() та
та![]() від
від![]()
до
![]() ;
;
2)
![]() .
Знайти
.
Знайти![]() .
.
4.11. Знайти повний
приріст і диференціал функції
![]() ,
якщо
,
якщо![]() змінюється від 2 до 2,1, а
змінюється від 2 до 2,1, а![]() від 1
до 1,2.
від 1
до 1,2.
4.12. Обчислити наближено:
|
1) |
|
2) |
|
|
3) |
|
4) |
|
|
5) |
|
6) |
|
|
7) |
|
8) |
|
|
9) |
|
10) |
|
|
11) |
|
|
|
4.13. Циліндричний
стакан має внутрішні розміри: радіус
основи
![]() м,
висоту
м,
висоту![]() м
і товщину стінок
м
і товщину стінок![]() =1дм.
Знайти наближено об’єм матеріалу,
витраченого на виготовлення стакану.
=1дм.
Знайти наближено об’єм матеріалу,
витраченого на виготовлення стакану.
4.14. Прямокутний
паралелепіпед має розміри:
![]() м,
м,![]() м,
м,![]() м.
Знайти наближено величину зміни діагоналі
паралелепіпеда, якщо
м.
Знайти наближено величину зміни діагоналі
паралелепіпеда, якщо![]() збільшиться на 2 см,
збільшиться на 2 см,![]() -
на 1 см, а
-
на 1 см, а![]() зменшиться на 3 см.
зменшиться на 3 см.
4.15. У зрізаному конусі
радіуси основ
![]() см,
см,![]() см,
висота
см,
висота![]() см.
Як наближено зміниться об’єм конуса,
якщо
см.
Як наближено зміниться об’єм конуса,
якщо![]() збільшити на 2 мм,
збільшити на 2 мм,![]() -
на 3мм і
-
на 3мм і![]() зменшити на 1 мм ?
зменшити на 1 мм ?
4.16. Радіус основи
конуса дорівнює 10,2
![]() 0,1
см, твірна дорівнює 44,6
0,1
см, твірна дорівнює 44,6![]() 0,1
см. Знайти об’єм конуса і вказати похибку
розрахунку.
0,1
см. Знайти об’єм конуса і вказати похибку
розрахунку.
4.17. Для обчислення
питомої ваги тіла його зважують і
вимірюють його об’єм. Виявляється, що
вага
![]() г,
а об’єм
г,
а об’єм![]() см
см![]() при цьому межі похибок величин
при цьому межі похибок величин![]() і
і![]() дорівнюють
дорівнюють![]() 0,5
г,
0,5
г,![]() =1
см
=1
см![]() .
Визначити межу похибки
.
Визначити межу похибки![]() у питомій вазі
у питомій вазі![]() ,
обчисленій за цими даними.
,
обчисленій за цими даними.
Диференціювання складних функцій
4.18. Дано
![]() .
Знайти
.
Знайти![]() та
та![]() .
.
4.19. Дано
![]() .
Знайти
.
Знайти![]() та
та![]() ,
при цьому ввести проміжні змінні.
,
при цьому ввести проміжні змінні.
4.20. Дано
![]() .
Знайти
.
Знайти![]() та
та![]() .
.
4.21. Дано
![]() .
Знайти
.
Знайти
![]() .
.
4.22. Дано
![]() .
Знайти
.
Знайти![]() та
та![]()
![]() .
.
4.23. Дано
![]() .
Знайти
.
Знайти![]() .
.
4.24. Дано
![]() .
Знайти
.
Знайти![]() .
.
4.25. Дано
![]() .
Знайти
.
Знайти![]() .
.
4.26. Дано
![]() .
Знайти
.
Знайти
![]() .
.
4.27. Дано
![]() .
Знайти
.
Знайти![]() .
.
4.28. Дано
![]() .
Знайти
.
Знайти![]() .
.
4.29. Дано
![]() .
Знайти
.
Знайти
![]() та
та![]() .
.
4.30. Дано
![]() .
Знайти
.
Знайти![]() та
та![]() .
.
4.31. Дано
![]() .
Знайти
.
Знайти![]() .
.
4.32. Дано
![]() .
Знайти
.
Знайти![]() .
.
4.33. Дано
![]() .
Знайти
.
Знайти![]() та
та![]() .
.
4.34. Дано
![]() .
Знайти
.
Знайти![]() та
та![]() .
.
4.35. Дано
![]() .
Знайти
.
Знайти![]() та
та![]() .
.
4.36. Дано
![]() .
Знайти
.
Знайти![]() .
.
4.37. Рух точки задано
рівняннями
![]()
![]() .
З якою швидкістю зростає її відстань
від початку координат ?
.
З якою швидкістю зростає її відстань
від початку координат ?
