8. Пост. Задачі чис-го інтег-ня. Чисельне інтегрування ф-ї однієї змінної м-м прямокутників, трапецій та методом Сімпсона. Похибки цих методів.

Нехай задано, що ф-я f(x) – неперервна на [a;b], розгул. інтеграл:I=.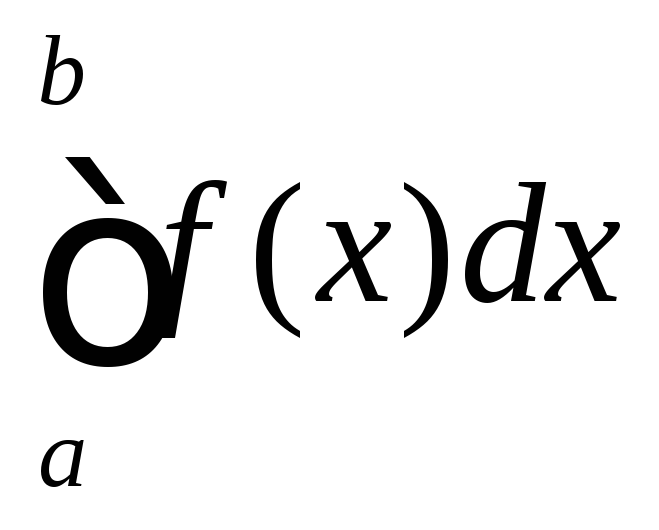

Формули прямокутників

При виведенні квадратурних формул викор. означеня визначеного інтеграла

I=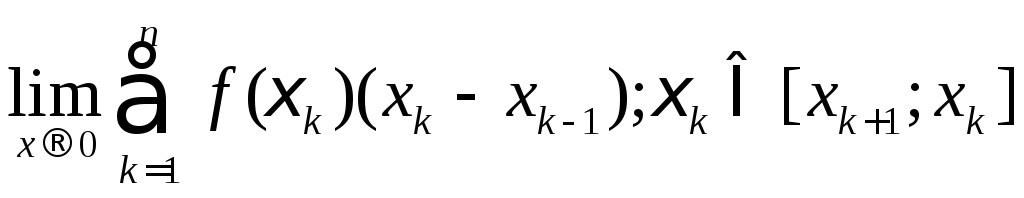

При чому, ця границя не залежить від способу розбиття відрізка [a;b] наn– частин і від способу вибору т.. За квадратурну формулу приймаємо:

I=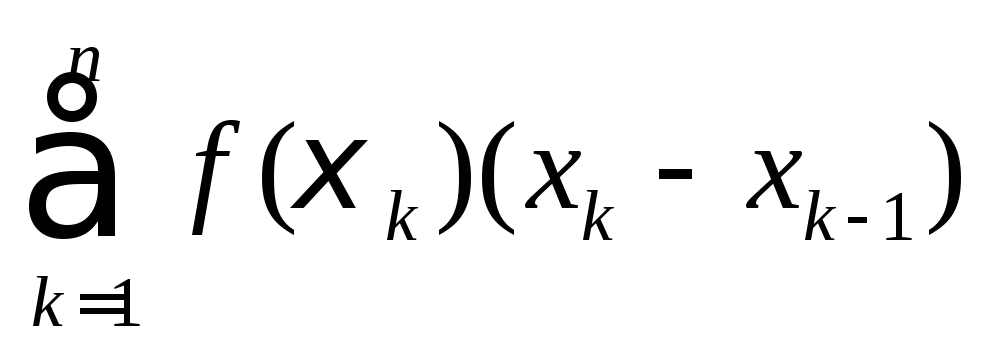 (1)

яка наз. заг. квадратурною ф. прямокутників.

Геометрична інтерпретація ф.(1) : площа криволінійної трапеції заміняється пощею ступінчастої фігури, яка склад. з прямокутників

О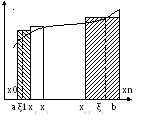скільки вибір розбиття і т.довільний, то нехай відстань між т.становитьh=, тоді квадратурна ф. (1) набуде вигляду:I=h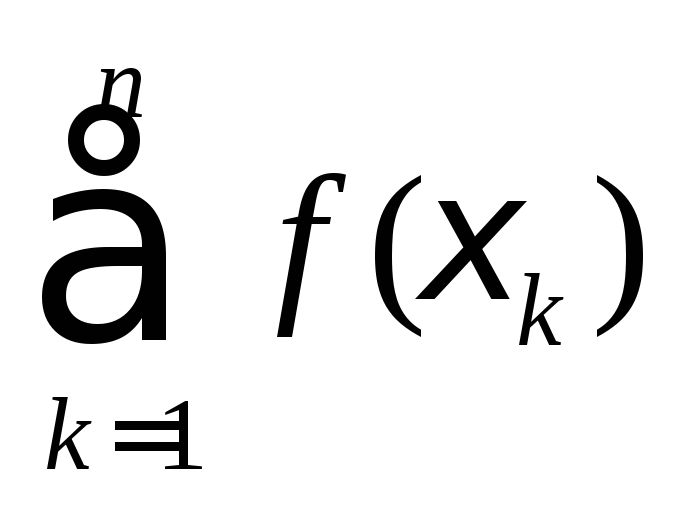

При дов. виборі т.можливі такі випадки:

1. Нехай 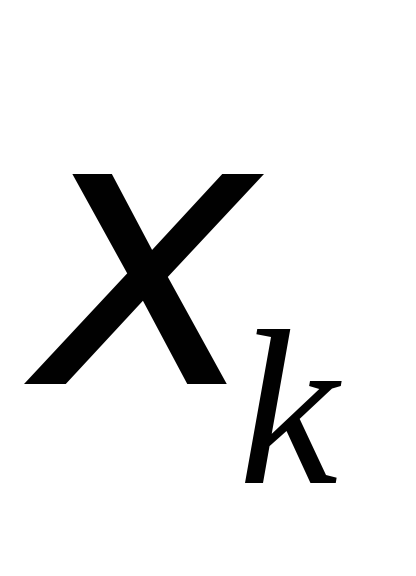=x_k-1, тоді квадрат. ф.:

I=h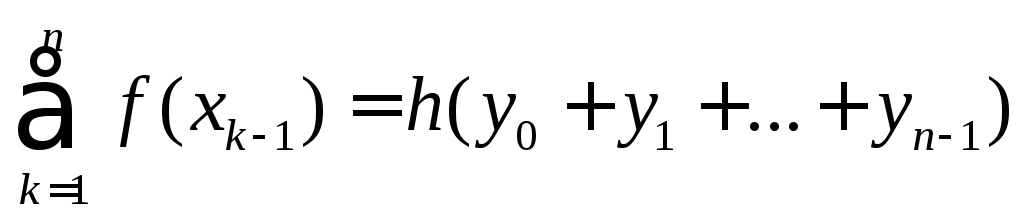- квадратурна ф. лівих прямокутників.

2) =x_k;I=h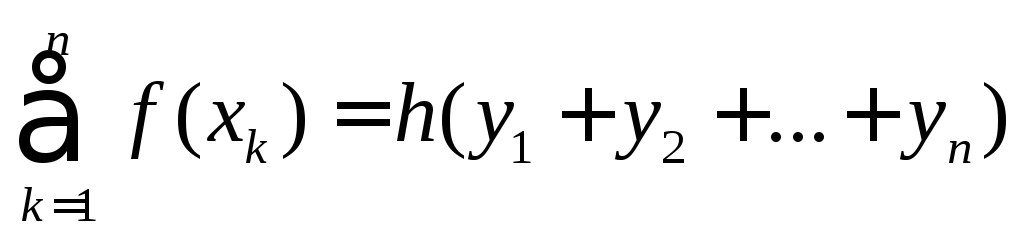- квадратурна ф. правих прямокутників.

3)I=h- квадрат. ф. серд. прямокутників.

Формули трапецій

Розглянемо відрізок [x_0, x₀+h] на якому ф-яf(x) двічі неперервно диференційована. Розглянемо інтеграл.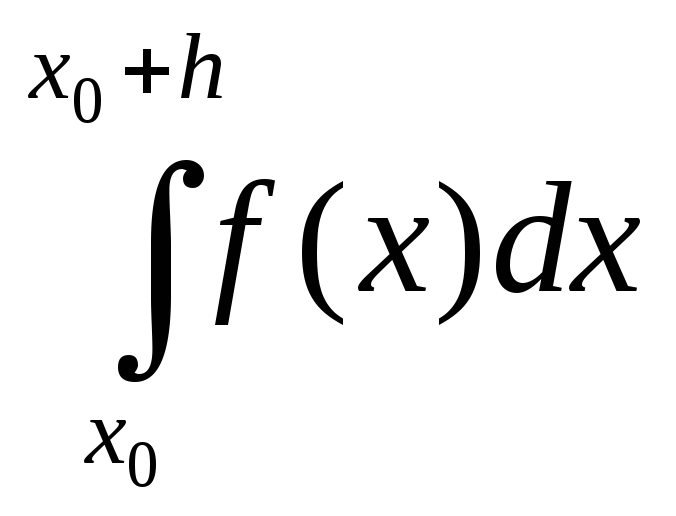

Формула Трапецій

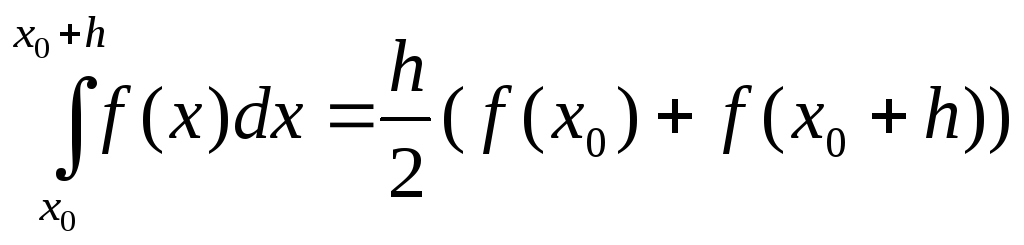(2)

Ф.(2) наз. квадратурною формулою трапецій.

Формула Сімпсона

Побудуємо триточкову квадратурну формулу з рівновіддаленими вузлами. Для цього розглянемо інтеграл

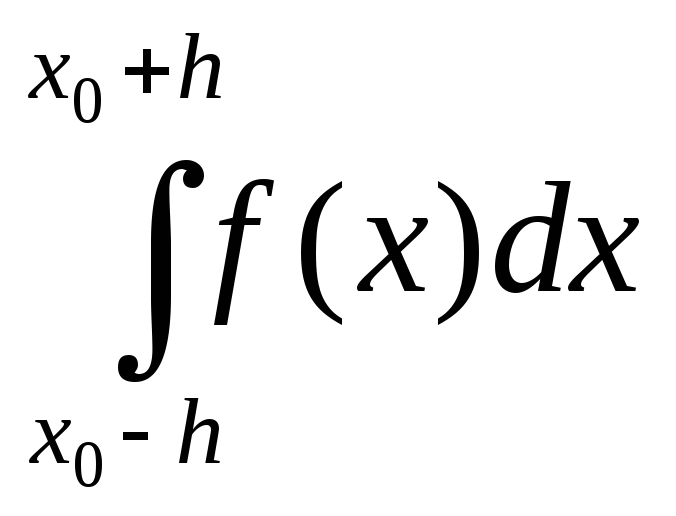, деf(x) – непер. на [x₀-h;x₀+h] разом з похідною до 4-го порядку включно. Використаємо інтерполяційний многочлен Лагранжа 2-го порядку, графік якого проходить через т.(x₀-h;f(x₀-h);x₀;f(x₀))i(x₀+h;f(x₀+h)) і про інтегруємо його у межах відx₀-hдоx₀+h. Тоді квадратурну формулу будуватимемо методом не визнач. коеф.:

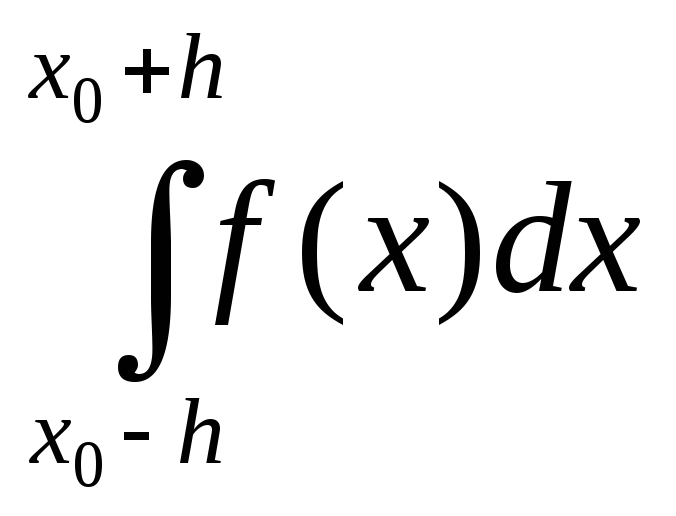=2h(A(f(x₀-h)+f(x₀+h))+Bf(x₀))+R(f) (3)

Де AіB– невідомі, аR(f) – залишковий член

Формала Сімпсона

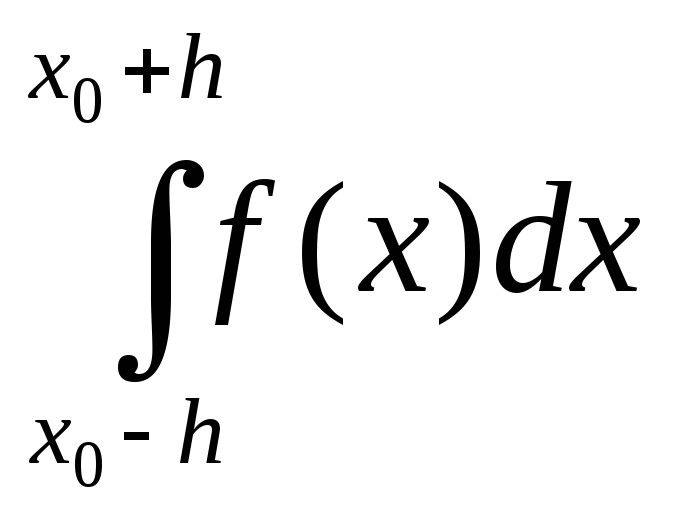=(4)

Оцінка похибки чисельного інтегрування за ф. Сімпсона (4) має вигляд:

, де

Узагальнену ф. Сімпсона

з оцінкою залишкового члена

, де

9. Метод Ейлера та його модифікації розв’язку задачі коші для звичайних диф. Р-нь. Геометричні ілюстрації цих методів.

Нехай дано ,а ф-яf(x,y) визначена на [a;b]. Поділимо цей відрізок наn-частин

;

Мал. 9.1

Розглянемо відрізокпро інтегруємо д. р. на цьому вілрізку

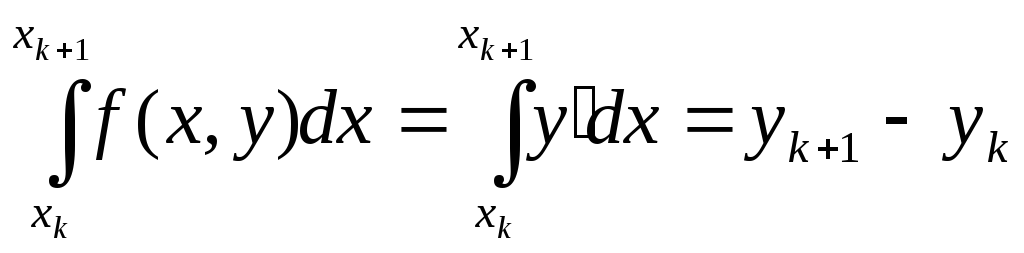
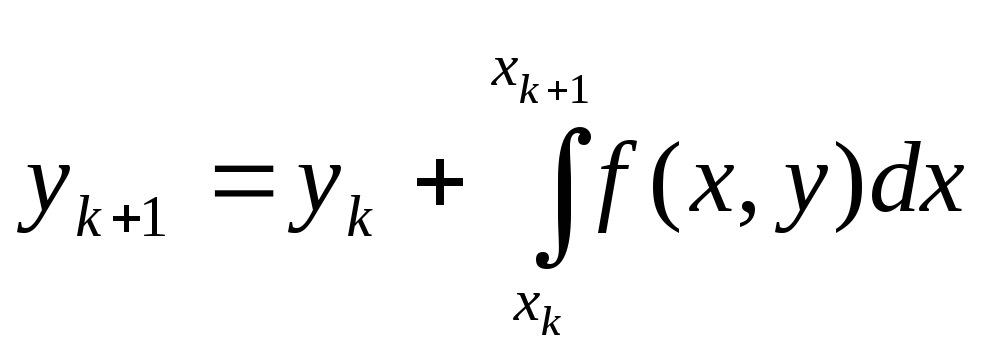
Якщо hмале то ф-юf(x;y) можна вважати сталою і вона приймає значення лівого кінця відрізка

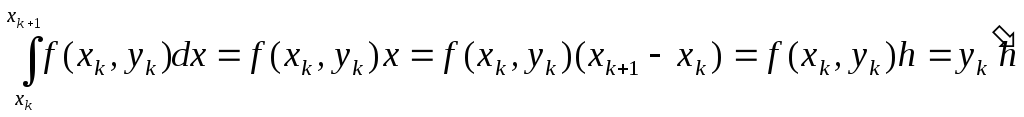
Отже знаходження наближеного розв’язку д.р. за схемою Ейлера відбув. за формулами

Обчислення y(x) за методом Ейлера зручно записувати у таблиці

i	xi	yi	yi′=f(xi,yi)	h yi′
(1)	(2)	(3)	(4)	(5)

1. Заповнимо перший рядок стовпців (1) (2) (3).

2. Обчислимо y_i^′і записуємо в стовпчик (4)

3. Обчислимо hy_i^′і записуємо в (5)

4. У стовпчик (3) другого рядка запишемо суму числа з стовпчика (3) і числа (5)

Модифікації:

1). Удосконалений метод Ейлера.

Реалізовують в два етапи.

Обчислюють координати середньої точки проміжка

Потім шукають

А

X=x₀ Y=y₀

Y=Y+hf(x,Y)

x=x+h

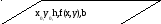
лгоритм методу Ейлера

- +